Среднее арифметическое описывается при помощи всего двух параметров меры положения и меры рассеяния
МЕРЫ ПОЛОЖЕНИЯ И МЕРЫ РАССЕЯНИЯ ЧАСТОТНОГО РАСПРЕДЕЛЕНИЯ И ИХ ХАРАКТЕРИСТИКА.
Ряды распределения описываются разными числовыми характеристиками, которые называются мерами. Меры – это числовые характеристики вариационного ряда.
Все меры делятся на три основные группы:
2. Меры рассеяния (разброса).
1. К мерам положения относятся различные средние значения.
Основные меры положения:
1. Мода Мо.
2. Медиана Ме.
3. 
Средняя арифметическая простая 
4. Средняя арифметическая взвешенная 
Более редко используются:
5. Средняя геометрическая.
6. Средняя гармоническая.
7. Средняя квадратичная.
8. Средняя кубическая.
Для нахождения медианы нужно:
1. Упорядочить (ранжировать) ряд в порядке возрастания числовых значений.
2. Найти номер медианы по формулам:
для нечетного числа вариантов (нечетного объема выборки) 
;
для четного числа вариантов (четного объема выборки) 
.
Средняя арифметическая простая 
— величина, полученная суммированием числовых значений всех вариантов с последующим делением суммы на объем совокупности. Средняя арифметическая простая находится по формуле:
Средняя арифметическая взвешенная 
– величина, полученная суммированием произведений числовых значений вариантов на их частоты с последующим делением суммы на объем совокупности. Формула вычисления средней взвешенной:
Пример: Обследовано 10 семей с числом детей в семье от 1 до 3 человек. Среднюю арифметическую числа детей в семье вычисляем как среднюю взвешенную соответственно данным таблицы:
| число детей хi |
| число семей с данным количеством детей Ni |
Меры рассеяния характеризуют разброс числовых значений вариантов в генеральной или выборочной совокупности относительно средних значений.
К мерам рассеяния относятся:
1. Вариационный размах R;
2. Индивидуальное отклонение d;
4. Стандартное отклонение (среднее квадратическое отклонение) σ, s ;
5. Коэффициент вариации V.
Основное свойство индивидуальных отклонений: сумма всех индивидуальных отклонений равна нулю.
Дисперсия генеральной совокупности обозначается σ 2 ( выборочной s 2 ) и вычисляется по формуле:
σ 2 = 
.
Стандартное отклонение генеральной совокупности обозначается символом σ ( выборки s ) и вычисляется по формуле:
Коэффициент вариации— это относительная мера рассеяния, равная отношению стандартного отклонения s к средней арифметической 
.
Коэффициент вариации обозначается символом V, вычисляется в долях единицы или в процентах по формулам:
.
Кроме вышеприведенных числовых характеристик вариационного ряда в статистике существуют и другие, но они в медицине практически не используются.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Характеристики рассеяния
Характеристики положения описывают центр распределения. В то же время значения вариант могут группироваться вокруг него как в широкой, так и в узкой полосе. Поэтому для описания распределения необходимо охарактеризовать диапазон изменения значений признака. Для описания диапазона варьирования признака используются характеристики рассеяния. Наиболее широкое применение нашли размах вариации, дисперсия, стандартное отклонение и коэффициент вариации.
Размах вариации определяется как разность между максимальным и минимальным значением признака в изучаемой совокупности:
Очевидным достоинством рассматриваемого показателя является простота расчета. Однако поскольку размах вариации зависит от величин только крайних значений признака, то область его применения ограничена достаточно однородными распределениями. В остальных случаях информативность этого показателя весьма невелика, поскольку существует очень много распределений, сильно отличающихся по форме, но имеющих одинаковый размах. В практических исследованиях размах вариации используется иногда при малых (не более 10) объемах выборки. Так, например, по размаху вариации легко оценить, насколько различаются лучший и худший результаты в группе спортсменов.
В рассматриваемом примере:
Второй характеристикой рассеяния является дисперсия. Дисперсия представляет собой средний квадрат отклонения значения случайной величины от ее среднего значения. Дисперсия есть характеристика рассеяния, разбросанности значений величины около ее среднего значения. Само слово «дисперсия» означает «рассеяние».
На первый взгляд наиболее естественной оценкой для дисперсии является статистическая дисперсия, вычисленная, исходя из определения, по формуле:
.
В этой формуле 
— сумма квадратов отклонений значений признака хi от среднего арифметического 
. Для получения среднего квадрата отклонений эта сумма поделена на объем выборки п.
Однако такая оценка не является несмещенной. Можно показать, что сумма квадратов отклонений значений признака для выборочного среднего арифметического меньше, чем сумма квадратов отклонений от любой другой величины, в том числе от истинного среднего (математического ожидания). Поэтому результат, получаемый по приведенной выше формуле, будет содержать систематическую ошибку, и оценочное значение дисперсии окажется заниженным. Для ликвидации смещения достаточно ввести поправочный коэффициент 
. В результате получается следующее соотношение для оценочной дисперсии:
.
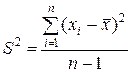
5 (15,385-14,5331) 2 +2 (16,055-14,5331) 2 ]/28=0,5473 (м 2 ).
Дисперсия случайной величины имеет размерность квадрата размерности случайной величины, что затрудняет ее интерпретацию и делает не очень наглядной. Для более наглядного описания рассеяния удобнее пользоваться характеристикой, размерность которой совпадает с размерностью исследуемого признака. С этой целью вводится понятие стандартного отклонения (или среднего квадратического отклонения).
Стандартным отклонением называется положительный корень квадратный из дисперсии:
.
В разбираемом нами примере стандартное отклонение равно
(м).
Стандартное отклонение имеет те же единицы измерения, что и результаты измерения исследуемого признака и, таким образом, оно характеризует степень отклонения признака от среднего арифметического. Иными словами, оно показывает, как расположена основная часть вариант относительно среднего арифметического.
Стандартное отклонение и дисперсия являются наиболее широко применяемыми показателями вариации. Связано это с тем, что они входят в значительную часть теорем теории вероятностей, служащей фундаментом математической статистики. Помимо этого, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов на вариацию исследуемого признака.
Помимо абсолютных показателей вариации, которыми являются дисперсия и стандартное отклонение, в статистике вводятся относительные. Наиболее часто применяется коэффициент вариации. Коэффициент вариации равен отношению стандартного отклонения к среднему арифметическому, выраженному в процентах:
.
Из определения ясно, что по своему смыслу коэффициент вариации представляет собой относительную меру рассеяния признака.
Для рассматриваемого примера:
.
Коэффициент вариации широко используется при проведении статистических исследований. Будучи величиной относительной, он позволяет сравнивать колеблемости как признаков, имеющих различные единицы измерения, так одного и того же признака в нескольких разных совокупностях с различными значениями среднего арифметического.
Коэффициент вариации используется для характеристики однородности полученных экспериментальных данных. В практике физической культуры и спорта разброс результатов измерений в зависимости от значения коэффициента вариации принято считать небольшим (V 20%).
Ограничения на использование коэффициента вариации связаны с его относительным характером – определение содержит нормировку на среднее арифметическое. В связи с этим при малых абсолютных значениях среднего арифметического коэффициент вариации может потерять свою информативность. Чем ближе значение среднего арифметического к нулю, тем менее информативным становится этот показатель. В предельном случае среднее арифметическое обращается в ноль (например, температура) и коэффициент вариации обращается в бесконечность независимо от разброса признака. По аналогии со случаем погрешности можно сформулировать следующее правило. Если значение среднего арифметического в выборке больше единицы, то использование коэффициента вариации правомерно, в противном случае для описания разброса опытных данных следует использовать дисперсию и стандартное отклонение.
В заключение этой части рассмотрим оценку варьирования значений оценочных характеристик. Как уже было отмечено, значения характеристик распределения, рассчитанные по данным эксперимента, не совпадают с их истинными значениями для генеральной совокупности. Точно установить последние не представляется возможным, поскольку, как правило, невозможно обследовать всю генеральную совокупность. Если использовать для оценки параметров распределения результаты разных выборок из одной и той же генеральной совокупности, то окажется, что эти оценки для разных выборок отличаются друг от друга. Оценочные значения флуктуируют около своих истинных значений.
,
Поскольку истинное значение стандартного отклонения не известно, то для оценки стандартного отклонения выборочного среднего используется величина, называемая стандартной ошибкой среднего арифметического и равная:
.
Величина 
характеризует ошибку, которая в среднем допускается при замене генерального среднего его выборочной оценкой. Согласно формуле, увеличение объема выборки при проведении исследования приводит к уменьшению стандартной ошибки пропорционально корню квадратному из объема выборки.
Для рассматриваемого примера значение стандартной ошибки среднего арифметического равно 
. В нашем случае она оказалась в 5,4 раза меньше значения стандартного отклонения.
Характеристики формы
При проведении статистических исследований встречаются распределения, имеющие самые разнообразные формы. Для характеристики отклонения формы распределения от симметричной используется коэффициент асимметрии или просто асимметрия, обозначаемая As и вычисляемая по формуле:
,
— среднее арифметическое;
Для симметричной формы распределения коэффициент асимметрии равен нулю. На рис. 8 и 9. показано два асимметричных распределения. Одно из них (рис. 8) имеет положительную асимметрию (As>0), а другое (рис. 9) – отрицательную (As 3 +8 (14,045-14,5331) 3 +10 (14,715-14,5331) 3 +
5 (15,385-14,5331)5 3 +2 (16,055-14,5331) 3 ]/[29* 0,7398 3 ]= 0,260663.
Коэффициент асимметрии положителен, следовательно, можно предположить, что распределение признака в генеральной совокупности имеет левостороннюю асимметрию.
.
Нормировка на среднее квадратическое отклонение S производится для обезразмеривания, что необходимо для сравнительного анализа степени асимметрии различных распределений. Применение этого показателя основано на том, что равенство среднего арифметического, моды и медианы имеет место только для симметричных распределений. Поэтому наиболее просто связать показатель асимметрии с соотношением характеристик положения: чем больше разница между средним арифметическим и модой, тем больше асимметрия распределения. В нашем примере:
.
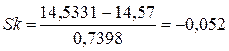
Как видим, и мера скошенности имеет значение, близкое к нулю. В рассматриваемом случае As>0, а Sk 4 +8 (14,045-14,5331) 4 +10 (14,715-14,5331) 4 +
Отрицательное значение эксцесса свидетельствует о наличии тенденции к плосковершинности у рассматриваемого эмпирического распределения.
Меры положения и рассеяния кривой распределения
Кривая распределения плотностей вероятностей случайной величины характеризуется своим положением на оси абсцисс и рассеиванием случайной величины. Для оценки положения и рассеяния кривой распределения вводятся соответствующие критерии или меры.
К мерам положения относятся: мода, математическое ожидание и медиана случайной величины.
К мерам рассеяния относятся: стандартное отклонение, дисперсия и размах.
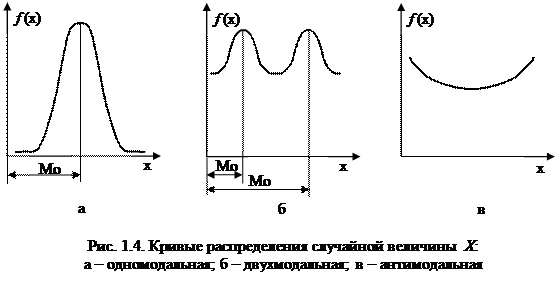
Функция распределения плотности вероятностей может иметь одно или несколько максимальных значений в разных местах области (рис. 1.4). Значение случайной величины X, при котором f(x)принимает максимальное (наиболее вероятное) значение в окрестности какого-либо значения случайной величины х, называется модой распределения (Mо).
Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений
Это определение справедливо для дискретных случайных величин. Для непрерывных величин математическое ожидание случайной величины X, имеющей плотность распределения f(х), вычисляется по формуле
Статистической оценкой математического ожидания является среднее арифметическое значение случайной величины
Математическое ожидание (среднее арифметическое значение) случайной величины называют часто центром рассеяния или центром группирования случайной величины. Математическое ожидание является оценкой истинного значения измеряемой величины. Медианой (Ме) случайной величины называется значение, для которого
|
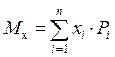.(1.5)
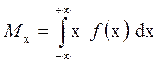.(1.6)
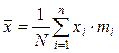.(1.7)
.
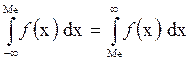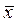служит стандартное (или среднее квадратическое) отклонение s
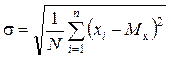. (1.8)
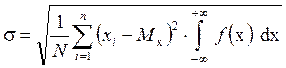. (1.9)
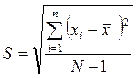. (1.10)
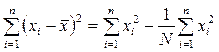. (1.10¢)
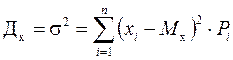, (1.11)
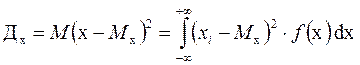, (1.11¢)
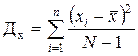. (1.11»)
.
,
,
.
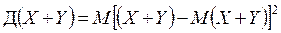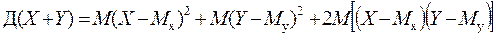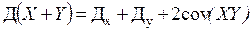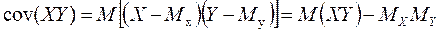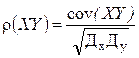. (1.12)
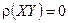. Если абсолютное значение ρ(ХY) окажется больше 1, то совершенно ясно, что произошла ошибка и необходимо пересчитать результат. В случае сильной положительной корреляции достигается значение, близкое к +1, а при сильной отрицательной корреляции достигается значение, близкое к –1. Таким образом, когда |ρ(ХY)| близок к 1, это указывает на сильную корреляцию между X и Y, а когда |ρ(ХY)| близок к 0 – на слабую корреляцию.
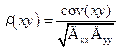, (1.12′)
;
; 
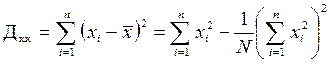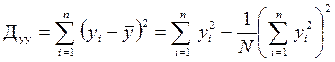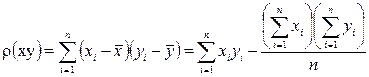; n – число пар данных.
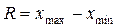.(1.13)
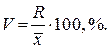(1.14)