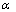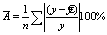Стандартная ошибка параметров регрессии
Оценка результатов линейной регрессии
Введение
Модель линейной регрессии
Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так: 
где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.
Функция summary.lm() и оценка получившихся результатов
Теперь рассмотрим пример построения модели линейной регрессии в языке R:
Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.
Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат: 
при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0: 
где

Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.
В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.
Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.
А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared: 
где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.
Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.
Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:
Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.
Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы: 
Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().
Заключение
В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его величина сравнивается с
его стандартной ошибкой, т. е. определяется фактическое значение t-критерия
Стьюдентa: 
затем сравнивается с табличным значением при определенном уровне значимости
и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:

Значимость линейного коэффициента корреляции проверяется на основе величины
ошибки коэффициента корреляции тr:

Общая дисперсия признака х:
Коэф. регрессии 
величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации:
16. Оценка значимости параметров уравнения множественной регрессии
Множественная регрессия-это уравнение связи с несколькими независимыми переменными
Экономический смысл параметров множественной регрессии
Коэффициент множественной регрессии bj показывает, на какую величину в среднем изменится результативный признак Y, если переменную Xj увеличить на единицу измерения, т. е. является нормативным коэффициентом.
Матричная запись множественной линейной модели регрессионного анализа:
Модель множественной регрессии вида Y = b0 + b1X1 + b2X2;
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов.
Как и в случае множественной регрессии, статистическая значимость коэффициентов множественной регрессии с m объясняющими переменными проверяется на основе t-статистики:

имеющей в данном случае распределение Стьюдента с числом степеней свободы v = n- m-1. При требуемом уровне значимости наблюдаемое значение t-статистики сравнивается с критической точной 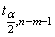
В случае, если 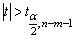
Формула средней ошибки параметра зависит от какого параметра оценивается. Общая для всех параметров уравнения регрессии формула выглядит следующим образом:
Mbi=квадратный корень из SSост./n-m-1 * [X в степени T * X] в минус первой степени) ii
SSост. = E(y-y с домиком) в квадрате
n – число наблюдений
m – количество параметров без свободного члена.
0 (0)
Квадратный корень из SSост.\n-m-1 – стандартная ошибка регрессии
В большинстве случаев приведённую формулу ошибки можно упростить, в частности, если имеется парное линейное уравнение регрессии, то ошибка коэффициента регрессии рассчитывается по формуле:
Mb = квадратный корень из SSост.\ (n-m-1) * E (x – x c штрихом) в квадрате
Ma = квадратный корень из SSост. * Ex в квадрате\ (n-m-1) * E ( x – x с штрихом) в квадрате * n
Mbi= Gy/Gx * квадратный корень из 1-R в квадрате \ ( 1 – R в квадрате xi(x)) – (n-m-1)
Для определения ошибки собственного члена не подходит.
R в квадрате xi (x) = r в квадрате
Общий критерий Фишера
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F-критерия. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения, т.е. критерий F:
F= Dфакт/Dост = (R²/1-R²) * (n-m-1/m),
где Dфакт – факторная сумма квадратов на одну степень свободы
n – число наблюдений
m – число параметров при переменных x (в линейной регрессии совпадает с числом включенных в модель факторов)
Dост – остаточная сумма квадратов на одну степень свободы.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n-m-1) – число степеней свободы для остаточной суммы квадратов.
Применение критерия Фишера предполагает:
1) расчет фактического значения критерия Fфакт
2) по таблице – табличного значения Fтабл
3) сравнение Fфакт и Fтабл, если факт>табл, то оцениваемое уравнение регрессии значимо с вероятностью P= 1-a (альфа), где а- вероятность ошибки.

SSост – остаточная сумма квадратов = 
Табличное значение F-критерия – это максимальная величина отношения дисперсий.
Формулу фактического значения часто используют в измененном виде:
Таблица дисперсионного анализа
Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа.
| Источники вариации | Число степеней свободы df | Сумма квадратов отклонений | Дисперсия на одну степень свободы (MS=SS/df) | Fфакт | Fтабл, при а=0,05 |
| Регрессия | m | SSфакт = ∑(y^-y¯)² | SSфакт/m | MSфакт/ MSост | Fтабл |
| Случайные колебания | n-m-1 | SSост = ∑(y-y^)² | SSост/ n-m-1 | — | — |
| Общая вариация | n-1 | SSобщ = ∑(y-y¯)² | — | — | — |
19.Показатели частной корреляции и детерминации
Для оценки изолирован влияния кажд фактора на рез-т при устранении воздействия прочих факторов модели исп-ся частные показатели корреляции. Показатели частн корреляц представляют собой отношение сокращения остаточной дисперсии за счет дополнит включения в анализ нов фактора к остаточн дисперсии, имевшей место до введения его в модель. 1)индекс частной корреляции для фактора х1. η yx1*x2x3…xn=корень из (G 2 yx2x3..xm(ост) – G 2 yx1x2x3..xm(ост))/G 2 yx2x3..xm(ост) Под корнем в числителе- сокращение остаточн дисперсии за счет включения в модель фактора x1 после остальных факторов. 2)частный коэф корреляции ryx1*x2x3..xm=корень из (1-(1– R 2 yx1*x2x3..xm)/(1- R 2 yx2x3..xm))Рекурентные формулы расчета частн коэф корреляции 1го порядка: Порядок частн показателя корреляции соотв-ет числу факторных признаков, влияние котор устраняется. Для 2х факторн модели част коэф корреляции:
20. Частный F-критерий
Для оценки статистич целесообразности добавления нов факторов в регрессион модель исп-ся частн критерий Фишера, т.к на рез-ты регрессион анализа влияет не только состав факторов, но и последовательность включения фактора в модель. Это обьясняется наличием связи между факторами.
Fxj =( (R 2 по yx1x2. xm – R 2 по yx1x2…xj-1,хj+1…xm)/(1- R 2 по yx1x2. xm) )*( (n-m-1)/1)
Fтабл (альфа,1, n-m-1) Fxj больше Fтабл – фактор xj целесообразно лючать в модель после др.факторов.
Если рассматривается уравнение y=a+b1x1+b2+b3x3+e, то определяютсяпоследовательно F-критерий для уравнения с одним фактором х1, далее F-критерий для дополнительного включения в модель фактора х2, т. е. дляперехода от однофакторного уравнения регрессии к двухфакторному, и,наконец, F-критерий для дополнительного включения в модель фактора х3, т.е. дается оценка значимости фактора х3 после включения в модель факторов x1их2. В этом случае F-критерий для дополнительного включения фактора х2после х1 является последовательным в отличие от F-критерия длядополнительного включения в модель фактора х3, который является частным F-критерием, ибо оценивает значимость фактора в предположении, что он включенв модель последним. С t-критерием Стьюдента связан именно частный F-критерий. Последовательный F-критерий может интересовать исследователя настадии формирования модели. Для уравнения y=a+b1x1+b2+b3x3+e оценказначимости коэффициентов регрессии Ь1,Ь2,,b3 предполагает расчет трехмежфакторных коэффициентов детерминации.
Тест Парка
Тест Парка – нахождение параметров для регрессии следующего вида:
Оцен-ся значимость коэффициента b (знач, если t факт>t табл),
если значимый – остатки гетероскедастичны,
если незначим – гомоскед.
Тест Глейзера
а,b – неизвестные параметры, зависят от ур. регрессии
Дается оценка значимости b, если он значим – гетероскедостичность в остатке (т.е. отсутствие зависимости x от y)
Тест Уайта.
используется для анализа гетероскедастичности случайных остатков (E).
Т.е. изменения дисперсии случайных остатков от наблюдения к наблюдению.
Для выбора хорошей модели уравнения регрессии необходимо, чтобы Е были гомоскедастичны, т.е. их дисперсия была постоянна, и не зависела от дисперсии фактора х.
В тесте Уайта моделируется уравнение рессии,сост. из элементов, включающих все факторы, входящие в уравнение регрессии+Эти же факторы в квадрате+необязательная часть,- попарные произведения факторов.
Для случая модели с двумя факторами (x1 и x2), ур-я будут иметь вид:
В рамках теста нужно оценить знач-ть всего ур. в целом, с помощью F-критерия Фишера. Если Fфакт>Fтабл =>Ур. значимо => все ф-ры оказывают влияние на величину Е и => остатки гетероскед-ны. И наоборот.
Тест Гольдфельда-Квандта.
С помощью этого теста исследуются случайные остатки (Е) на предмет гомоскедастичности.
Например: Отсортируем совок-ть по фактору x2(он предположит-но влияет на Е)
Стандартная ошибка
В случае несмещенного оценщика стандартная ошибка, следовательно, является мерой среднего отклонения оцененного значения параметра от истинного значения параметра. Чем меньше стандартная ошибка, тем точнее неизвестный параметр можно оценить с помощью оценщика. Стандартная ошибка зависит, помимо прочего, от
Как правило, чем больше размер выборки, тем меньше стандартная ошибка; чем меньше дисперсия, тем меньше стандартная ошибка.
оглавление
интерпретация
Стандартная ошибка дает представление о качестве оцениваемого параметра. Чем больше имеется индивидуальных значений, тем меньше стандартная ошибка и тем точнее можно оценить неизвестный параметр. Стандартная ошибка делает измеренный разброс (стандартное отклонение) двух наборов данных с разными размерами выборки сопоставимым путем нормализации стандартного отклонения к размеру выборки.
пример
обозначение
оценивать
Доверительные интервалы и тесты
или сформулировать тесты, например Б. принимает ли параметр определенное значение : ϑ 0 <\ displaystyle \ vartheta _ <0>>
ЧАС 0 : ϑ знак равно ϑ 0 <\ displaystyle H_ <0>: \ vartheta = \ vartheta _ <0>> 
а результаты статистики теста:
Стандартная ошибка среднего арифметического
Стандартная ошибка среднего арифметического такая же
σ ( Икс ¯ ) знак равно σ п <\ Displaystyle \ sigma (<\ overline 
Вывод
Икс ¯ знак равно 1 п ∑ я знак равно 1 п Икс я <\ displaystyle <\ overline
σ ( Икс ¯ ) 2 знак равно Вар ( Икс ¯ ) знак равно Вар ( 1 п ∑ я знак равно 1 п Икс я ) знак равно 1 п 2 Вар ( ∑ я знак равно 1 п Икс я ) знак равно 1 п 2 ∑ я знак равно 1 п Вар ( Икс я ) знак равно 1 п 2 п σ 2 знак равно σ 2 п <\ displaystyle \ sigma (<\ overline
σ ( Икс ¯ ) 2 знак равно 1 п 2 ∑ я знак равно 1 п σ я 2 <\ displaystyle \ sigma (<\ overline 
Предполагая выборочное распределение, стандартная ошибка может быть рассчитана с использованием дисперсии выборочного распределения:
пример
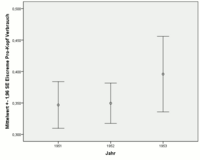
Для данных по мороженому рассчитывались среднее арифметическое, стандартная ошибка и стандартное отклонение за 1951, 1952 и 1953 годы для потребления мороженого на душу населения (измеряемого в пинтах ).
| год | В среднем | Стандартная ошибка среднего | Стандартное отклонение | Количество наблюдений |
|---|---|---|---|---|
| 1951 г. | 0,34680 | 0,01891 | 0,05980 | 10 |
| 1952 г. | 0,34954 | 0,01636 | 0,05899 | 13-е |
| 1953 г. | 0,39586 | 0,03064 | 0,08106 | 7-е |
Для 1951 и 1952 годов расчетные средние значения и стандартные отклонения, а также числа наблюдений примерно одинаковы. Следовательно, оцененные стандартные ошибки также дают примерно такое же значение. В 1953 г., с одной стороны, количество наблюдений меньше, а стандартное отклонение больше. Таким образом, стандартная ошибка почти вдвое превышает стандартные ошибки 1951 и 1952 годов.
Здесь также ясно видно, что среднее значение для 1953 г. может быть оценено более неточно, чем средние значения для 1951 и 1952 гг. (Более длинная полоса для 1953 г.).
Стандартная ошибка коэффициентов регрессии в модели простой регрессии
Пример : Для данных по мороженому была проведена простая линейная регрессия для потребления мороженого на душу населения (измеренного в поллитрах) со средней недельной температурой (в градусах Фаренгейта) в качестве независимой переменной. Оценка регрессионной модели привела к:
Потребление на душу населения знак равно 0,206 86 + 0,003 11 ⋅ температура <\ displaystyle <\ text <Потребление на душу населения>> = 0 <,>20686 + 0 <,>00311 \ cdot <\ text <Температура>>> 
| модель | Нестандартизированные коэффициенты | Стандартизированные коэффициенты | Т | Sig. | |
|---|---|---|---|---|---|
| Коэффициенты регрессии | Стандартная ошибка | ||||
| постоянный | 0,20686 | 0,02470 | 8,375 | 0,000 | |
| температура | 0,00311 | 0,00048 | 0,776 | 6,502 | 0,000 |
Хотя расчетный коэффициент регрессии для средней недельной температуры очень мал, расчетная стандартная ошибка дала еще меньшее значение. Точность оценки коэффициента регрессии в 6,5 раз меньше, чем самого коэффициента.