Связь угловых и линейных параметров вращающегося тела
Учебники
Журнал «Квант»
Общие
Чивилёв В.И. Кинематика вращательного движения //Квант. — 1986. — № 11. — С. 17-18.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Содержание
Медленно проехав перекресток, троллейбус стал удаляться по улице, плавно увеличивая свою скорость.
Движение колеса троллейбуса — лишь один из многих примеров сложного механического движения в окружающем нас мире. Оказывается, любое сложное движение можно представить как сумму двух простых движений — поступательного и вращательного. Понимать это следует так: всегда можно подобрать такую поступательно движущуюся систему отсчета, относительно которой движение выглядит только как вращение вокруг некоторой неподвижной оси.
Какую же в нашем случае надо выбрать систему отсчета, чтобы в ней колесо троллейбуса совершало чистое вращение? Какими физическими величинами описывается это вращение, как эти величины связаны друг с другом и как зависят от времени? Такие вопросы могут возникнуть не только на пешеходном переходе, но и на уроке, экзамене, при решении конкретной задачи.
На первый вопрос ответить легко, догадавшись, что поступательно движущуюся систему отсчета можно связать с самим троллейбусом (его корпусом). Перед тем как ответить на остальные вопросы, заметим, что в нашем примере колесо вращается неравномерно — модуль скорости любой точки колеса меняется со временем.
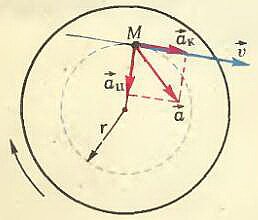
Рассмотрим некоторую точку М колеса, находящуюся на расстоянии r от оси вращения и имеющую в некоторый момент времени скорость \(
\vec \upsilon\) и ускорение \(
\vec a\) (рис. 1). Из физических соображений разумно ускорение \(
\vec a\) представить как сумму двух составляющих: одна из них \(
\vec a_c\) направлена по радиусу к центру окружности — центростремительное ускорение, вторая \(
\vec a_k\) направлена по касательной к окружности — касательное ускорение. Оба эти ускорения имеют определенный физический смысл — касательное ускорение характеризует быстроту изменения модуля скорости, а центростремительное характеризует быстроту изменения направления скорости. Можно показать, что модуль центростремительного ускорения \(
a_c = \frac<\upsilon^2>
a_k = \frac<\Delta \upsilon><\Delta t>\), где Δυ — изменение модуля υ скорости точки за сколь угодно малое время Δt.
Линейные и угловые величины
Как уже говорилось, нам надо ввести такие физические величины, которые характеризовали бы неравномерное вращение колеса (в системе отсчета, связанной с троллейбусом). Попробуем это сделать по аналогии с прямолинейным неравномерным движением.
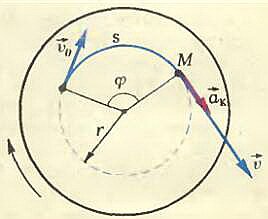
Проследим за точкой М колеса в течение малого промежутка времени Δt. За это время точка пройдет по дуге окружности путь s и будет иметь скорость υ и касательное ускорение ak (рис. 2). Три величины s, υ и ak, называемые линейными величинами, характеризуют движение точки М, но не могут служить для описания вращения всего колеса, так как в один и тот же момент времени другие точки, расположенные на других расстояниях от оси вращения, имеют другие линейные скорости, и касательные ускорения и пройденные ими пути тоже не одинаковы. Поэтому кроме линейных вводятся так называемые угловые величины, которые одинаковы для всех точек вращающегося колеса: угол поворота φ радиуса, соединяющего точку М с центром окружности, угловая скорость \(
\omega = \frac<\Delta \varphi><\Delta t>\) (Δφ — изменение угла поворота за время Δt) и угловое ускорение \(
\varepsilon = \frac<\Delta \omega><\Delta t>\) (Δω — изменение угловой скорости).
Очевидно, что введенными здесь угловыми величинами можно описывать вращение не только троллейбусного колеса, но и любого другого тела. При этом с течением времени может изменяться не только угол поворота φ, но и угловая скорость ω и угловое ускорение ε. В частности, если угловое ускорение не зависит от времени, то угловая скорость изменяется равномерно и в таком случае говорят, что имеет место равноускоренное вращение. Когда же угловая скорость остается постоянной, то угловое ускорение оказывается равным нулю и говорят о равномерном вращении тела.
Связь линейных и угловых величин
Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.
При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь
За малое время Δt точка проходит расстояние \(
Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть \(
Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.
Формулы кинематики для равноускоренного вращательного движения
Найдем зависимость угловой скорости ω и угла поворота φ колеса троллейбуса от времени t для случая вращения колеса с постоянным угловым ускорением ε.
Пусть начальная угловая скорость равна ω0. Тогда точка М, имея начальную скорость υ0 = rω0, будет двигаться с постоянным по модулю касательным ускорением ak = rε. По аналогии с прямолинейным равноускоренным движением для линейной скорости υ и пути s получим равенства
из которых после исключения времени t следует полезное соотношение:
Это и есть формулы кинематики для. вращательного движения любого тела (а не только колеса троллейбуса) с постоянным угловым ускорением.
Вращательное движение
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) ?,
скорость u — угловая скорость ?,
ускорение a — угловое ускорение ?
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад).
Если
? — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
Соотношение между единицами угла
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ? от t). 
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость ? от t) и график углового ускорения (зависимость ? от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
? — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
? — угловая частота,
то
Период
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2?:
Угловая скорость
Из формулы для одного оборота следует:
Обратите внимание:
• формулы справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
Равномерное движение тела по окружности
Говорят, что тело движется по окружности равномерно, если его угловая скорость постоянна, т.е. тело за равные промежутки времени поворачивается на один и тот же угол.
? — угловая скорость (постоянная в течение времени t)
? — угловое перемещение
t — время поворота на угол ?
Поскольку на графике угловой скорости площадь прямоугольника соответствует угловому перемещению, имеем:
Постоянная угловая скорость — есть отношение углового перемещения (угла поворота) ко времени, затраченному на это перемещение.
Единица СИ угловой скорости:
Равномерно ускоренное движение по окружности без начальной угловой скорости
Тело начинает двигаться из состояния покоя, и его угловая скорость равномерно возрастает.
? — мгновенная угловая скорость тела в момент времени t
? — угловое ускорение, постоянное в течение времени t
? — угловое перемещение тела за время t, (? в радианах)
t — время
Поскольку на графике скорости угловое перемещение равно площади треугольника, имеем:
Равномерно ускоренное движение по окружности с начальной угловой скоростью
Начальная скорость тела, равная ?0 в момент t = 0, изменяется равномерно на величину ??. (Угловое ускорение при этом постоянно.)
?0 — начальная угловая скорость
? — конечная угловая скорость
? — угловое перемещение тела за время t в радианах
t — время
? — угловое ускорение постоянное в течение времени t
Поскольку на графике скорости угловое перемещение соответствует площади трапеции под кривой скорости, имеем:
Так как площадь трапеции равна сумме площадей образующих ее треугольника и прямоугольника, получаем:
Далее из графика скорости следует
Совместив формулы мы получим
После преобразования получаем выражение, не содержащее времени:
Неравномерно ускоренное движение тела по окружности
Движение тела по окружности будет неравномерно ускоренным, если изменение угловой скорости происходит не пропорционально времени, т. е. если угловое ускорение не остается постоянным. В этом случае и угловая скорость и угловое ускорение являются функциями времени.
Связь величин ?, ? и ? представлена на соответствующих графиках.
Мгновенная угловая скорость
Полный угол поворота тела в любой момент времени можно определить по графику углового перемещения. Чем круче график, тем больше в данный момент времени мгновенная угловая скорость.
? — угол между касательной и осью времени t
? — мгновенная угловая скорость
? — угловое перемещение к моменту времени t

Мгновенной угловой скоростью называется первая производная функции ? = ?(t) по времени.
Обратите внимание:
1) чтобы вычислить мгновенную угловую скорость ?, необходимо знать зависимость углового перемещения от времени.
2) формула углового перемещения при равномерном движении тела по окружности и формула углового перемещения при равномерно ускоренном движении по окружности без начальной угловой скорости являются частными случаями формулы (2) соответственно для ? = 0 и ? = const.
Проинтегрировав обе части выражения, получим
Угловое перемещение есть интеграл по времени от угловой скорости.
Средняя угловая скорость
Средняя угловая скорость для некоторого интервала времени
Среднее число оборотов определяется аналогично формуле:
Вращательное движение тела, формулы
При вращательном движении твердого тела все элементы его массы, не лежащие на оси вращения, совершают движение по окружности. Аналогично и материальная точка, находящаяся на расстоянии r > 0 от оси вращения, также совершает движение по окружности, как и любое тело, достаточно удаленное от оси вращения.
Линейное перемещение Sл, линейная скорость uл и линейное ускорение aл при таком движении связаны между собой обычными для поступательного движения соотношениями.

Кроме того, эти величины связаны определенным образом с угловым перемещением ?, угловой скоростью ? и угловым ускорением ?.
| Sл | перемещение тела по траектории, | метр |
|---|---|---|
| Uл | скорость тела при движении по траектории, | метр / секунда |
| aл | ускорение данного тела при движении по траектории, | метр / секунда2 |
| r | радиус траектории, | метр |
| d | диаметр траектории, | метр |
| ? | угловое перемещение тела, | радиан |
| ? | угловая скорость тела, | радиан / секунда |
| ? | угловое ускорение тела, | радиан / секунда2 |
| f | частота, | Герц |
Примечание:Формулы справедливы для постоянных, мгновенных и средних величин, во всех случаях движения тела по окружности.
Векторные величины, характеризующие вращательное движение тела
| Угловая скорость и угловое ускорение тела являются векторными величинами. Эти векторы направлены вдоль оси вращения (аксиальные векторы), а их длина определяет величину соответствующих характеристик вращательного движения. Направление векторов определяется по правилу буравчика, т. е. совпадает с направлением поступательного движения буравчика, рукоятка которого движется в том же направлении, что и тело. |  |
Определение:Если тело участвует одновременно в нескольких вращательных движениях, то результирующая угловая скорость определяется по правилу векторного (геометрического) сложения:
Величина результирующей угловой скорости определяется по аналогии с формулой (Сложение движений):
или, если оси вращения перпендикулярны друг другу
Примечание: Результирующее угловое ускорение определяется аналогичным образом. Графически результирующую можно найти как диагональ параллелограмма скоростей или ускорений.
Связь между линейными и вращательными величинами
Физика > Связь между линейными и вращательными величинами
Охарактеризовать движение намного проще, если использовать угловую скорость, вращательную инерцию, вращательный момент и т.д.
Задача обучения
Основные пункты
Термины
Определение кругового движения
К характеристике кругового движения лучше всего подходить с позиции угловой величины. Например, мы сталкиваемся с равномерным круговым движением. Скорость частички меняется, хотя движение осуществляется равномерно. Эти понятия не увязываются, потому что равномерность ассоциируется с постоянством, но скорость всегда меняется.
Каждая частичка выполняет равномерное круговое движение вокруг стабильной оси. Лучше всего для описания использовать угловые величины
Если мы оперируем терминами угловой скорости, то подобные противоречия не возникают. Скорость постоянна. По сравнению с линейной скоростью угловая передает физический смысл вращения частицы, что указывает на поступательное движение. Угловое также демонстрирует разницу между поступательным и вращательным движениями.
Соотношение между линейной и угловой скоростями
Давайте взглянем на равномерное круговое перемещение. Для длины угла наклона дуги и радиуса круга получаем: s = rθ.
Из-за того, что = 0 для равномерного кругового движения, получаем v = ωr. Таким же образом выходим на a = αr, где a – линейное ускорение, а α – угловое (в более общем случае зависимость между угловыми и линейными величинами задается как v = ω × r, a = α × r + ω × v.)
Вращательные кинематические уравнения
С учетом линейной и угловой скоростей можно выйти на 4 вращательных кинематических уравнения для постоянных α:
Масса, импульс, энергия и второй закон Ньютона
Если располагаем массой, поступательной кинетической энергией, линейным импульсом и вторым законом Ньютона для описания линейного перемещения, то можно использовать соответствующие скалярные/векторные/тензорные величины для вращательного:
Для описания линейного движения применяется формула F = ma, поэтому можно использовать аналогичное τ = = r × F для описания углового. Они взаимозаменяемые и выбор делается исключительно для удобства расчетов.