Значение алгебраической дроби определено при условии что знаменатель не равен нулю
Решение уравнений с дробями
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Понятие дробного уравненияДробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так: Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе. Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры: На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное. Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение. Как решать уравнения с дробями1. Метод пропорцииЧтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает. Итак, у нас есть линейное уравнение с дробями: В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь. После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели. 2. Метод избавления от дробейВозьмем то же самое уравнение, но попробуем решить его по-другому. В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать: Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля! Вот так просто мы получили тот же ответ, что и в прошлый раз. Что еще важно учитывать при решенииУниверсальный алгоритм решенияОпределить область допустимых значений. Найти общий знаменатель. Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут. Раскрыть скобки, если нужно и привести подобные слагаемые. Решить полученное уравнение. Сравнить полученные корни с областью допустимых значений. Записать ответ, который прошел проверку. Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах. Примеры решения дробных уравненийЧтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек. Пример 1. Решить дробное уравнение: 1/x + 2 = 5. Пример 2. Найти корень уравнения Пример 3. Решить дробное уравнение: Если x = 3 — знаменатель тоже равен нулю. Понятие алгебраической дроби. Основное свойствоОпределение алгебраической дробиЧтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса). Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю). Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел. Алгебраические (рациональные) дроби Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных. Основное свойство алгебраической дробиПри умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь: Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например: Приведение алгебраических дробей к общему знаменателюОсновное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения: Алгоритм приведения алгебраических дробей к общему знаменателю Шаг 2. Дополнительные множители Перемена знака у члена дробиИз основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь: Дробь также не изменится, если провести следующие перемены знаков: Ещё несколько полезных формул, связанных с переменой знаков: ПримерыПример 1. Найдите допустимые значения переменных, входящих в дробь: $ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$ $ 3x-1 \neq 0 \iff x \neq \frac<1><3>$ $$ x- \frac<4> $ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff <\left\< \begin Пример 2. Сократите дроби: Пример 3. Упростите выражение: Пример 4. Постройте график функции: (О графике линейной функции – см. §38 справочника для 7 класса) Область определения функцииПрежде чем перейти к изучению области определения функции внимательно изучите уроки Вспомним кратко основные определения функции в математике. Функция — это зависимость переменной « y » от независимой переменной « x ». Функцию можно задать через формулу (аналитически). Например: Вместо « x » (аргумента функции) в формулу « у = 2x » подставляем произвольные числовые значения и по заданной формуле вычисляем Подставим несколько числовых значений вместо « x » в формулу « у = 2x » и запишем результаты в таблицу.
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции). Обозначают область определения функции как: Вернемся к нашей функции « у = 2x » и найдем её область определения. Посмотрим ещё раз на таблицу функции « y = 2x », где мы подставляли произвольные числа вместо « x », чтобы найти « y ».
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать, что вместо « x » мы могли подставлять любое действительное число. Другими словами, вместо « x » можно подставить любые числа, например: В нашей функции « у = 2x » вместо « x » можно подставить любое число, поэтому область определения функции « у = 2x » — это любые действительные числа. Запишем область определения функции « у = 2x » через математические обозначения. Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на математические символы. Для этого вспомним понятие числовой оси. Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции « у = 2x ». Так как в функции Запись выше читается как: « x » принадлежит промежутку от минус бесконечности до плюс бесконечности. Запишем окончательный ответ для области определения функции. По-другому промежуток Читается « x ∈ R » как: « x » принадлежит всем действительным числам». Область определения функции с дробьюРазберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе. № 233 (2) Мерзляк 8 классНайдите область определения функции: Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x » в функции
». По законам математики из школьного курса мы помним, что на ноль делить нельзя. Иначе говоря, знаменатель (нижняя часть дроби) не может быть равен нулю. Переменная « x » находится в знаменателе функции « f(x) =
». Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю. Получается, что « x » может принимать любые числовые значения кроме « −5 ». На числовой оси заштрихуем все доступные значения для « x ». Число « −5 » отмечено «пустой» точкой на числовой оси, так как не входит в область допустимых значений. Запишем заштрихованную область на числовой оси через знаки неравенства. Запишем промежутки через математические символы. Так как число « −5 » не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка. Вспомнить запись ответа через математические символы можно в уроке «Как записать ответ неравенства». Запишем окончательный ответ для области определения функции
». Область определения функции с корнемРассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень. № 98 (5) Колягин (Алимов) 8 классНайти область определения функции: Из урока «Квадратный корень» мы помним, что подкоренное выражение корня чётной степени должно быть больше или равно нулю. Найдём, какие значения может принимать « x » в функции Решим линейное неравенство по правилам урока «Решение линейных неравенств». Запишем полученный ответ, используя числовую ось и математические символы. Число « 6 » отмечено «заполненной» точкой на числовой оси, так как входит в область допустимых значений. Правило для определения области определения функцииЧтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики: При нахождении области определения функции необходимо всегда задавать себе два вопроса: Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа. Рассмотрим пример поиска области определения функции с корнем и дробью. № 242 (3) Мерзляк 8 классНайдите область определения функции: Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть. В функции « f(x) = √ x + 3 +
» есть дробь «
», где « x » расположен в знаменателе. Запишем условие, что знаменатель « x 2 − 9 » не может быть равен нулю. Решаем квадратное уравнение через формулу квадратного уравнения. x1;2 =
x1;2 =
x1;2 ≠
Запомним полученный результат. Задаем себе второй вопрос. Проверяем, есть ли в формуле функции
» корень четной степени. В формуле есть квадратный корень « √ x + 3 ». Подкоренное выражение « x + 3 » должно быть больше или равно нулю. Решим линейное неравенство. Объединим полученные ответы по обоим вопросам: Объединим все полученные результаты на числовых осях. Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям. Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях. Обратим внимание, что числа « −3 » и « 3 » отмечены «пустыми» точками и не входят в итоговое решение.
». Запишем окончательный ответ. Примеры определения области определения функции№ 101 Колягин (Алимов) 8 классНайти область определения функции: Для поиска области определения функций задаем себе первый вопрос. Есть ли знаменатель, в котором содержится « x »? Ответ: в формуле функции Задаем второй вопрос. Есть ли в функции корни четной степени? Ответ: в функции есть корень шестой степени: « 6 √ x ». Степень корня — число « 6 ». Число « 6 » — чётное, поэтому подкоренное выражение корня « 6 √ x » должно быть больше или равно нулю. В формуле функции « y = 6 √ x + 5 √ 1 + x » также есть корень пятой степени Получается, что единственное ограничение области определения функции Нарисуем область определения функции на числовой оси и запишем ответ. № 242 (4) Мерзляк 8 классНайдите область определения функции: Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два. Выделим знаменатели с « x » красным цветом. Запишем условие, что каждый из знаменателей не должен быть равен нулю.
Обозначим их номерами « 1 » и « 2 » и решим каждое уравнение отдельно.
Решаем первое уравнение. Если значение квадратного корня Теперь решим уравнение под номером « 2 », используя формулу квадратного уравнения. x1;2 =
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
В формуле функции
+
» есть два корня « √ x − 4 » и « √ x + 2 ». Их подкоренные выражения должны быть больше или равны нулю.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях. Выпишем результат решения системы неравенств. Объединим в таблицу ниже полученные ответы по обеим проверкам: Результат проверки, что знаменатели дробей с « x » не равны нулю Результат проверки, что подкоренные выражения должно быть больше или равны нулю Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет всем полученным условиям. Алгебраические дробиТема 7 «Алгебраические дроби» Цель главы – выработать у учащихся устойчивые навыки действий с алгебраическими дробями. Вы познакомитесь с алгебраическими дробями, у которых числитель и знаменатель — целые буквенные выражения, научитесь складывать, вычитать, умножать и делить алгебраические дроби. 1. Определение алгебраической дроби. В седьмом и восьмом классах рассматривались целые буквенные выражения. Такими выражениями являются многочлены от одной или нескольких переменных. Например, Иногда целые буквенные выражения называют целыми алгебраическими выражениями. Напомним, что при подстановке в целое алгебраическое выражение вместо букв некоторых чисел получается числовое выражение. Значение этого числового выражения называют значением целого алгебраического выражения при заданном наборе переменных. Например, целое выражение Целые буквенные выражения удобны для записи некоторых формул, функций и для других целей. 2. Значение алгебраической дроби. Для целых многочленов были определены сложение, вычитание и умножение. Изучая многочлены от одной переменной, мы установили, что разделить без остатка один многочлен на другой и получить частное в виде многочлена удается не всегда. Чтобы для буквенных выражений можно было рассмотреть деление, определяют алгебраические дроби. Отношение двух целых алгебраических выражений называется алгебраической дробью. Вот несколько примеров алгебраических дробей: У алгебраической дроби, как и у числовых дробей, имеются числитель и знаменатель. Числителем алгебраической дроби называют выражение, стоящее над дробной чертой. Знаменателем алгебраической дроби называют выражение, стоящее под дробной чертой. Для краткости алгебраическую дробь называют дробью, когда из текста ясно, о каких дробях идет речь. 3. Область определения дроби. Подставляя в алгебраическую дробь вместо букв конкретные числа, мы будем получать числовые выражения. При некоторых значениях переменных значение знаменателя может оказаться равным нулю. Но так как на нуль делить нельзя, то для таких значений переменных вычислить значение алгебраической дроби не удается. Будем говорить, что алгебраическая дробь не определена при наборах значений переменных, для которых значение знаменателя дроби равно нулю. Пример 1. Дробь Пример 2. Дробь Пример 3. Дробь 4. Так как алгебраическая дробь при некоторых значениях переменных может быть не определена, то это надо учитывать при действиях с дробями, рассматривая только такие значения переменных, для которых дроби определены и выполнимы все арифметические операции. Множество значений переменных, при которых данная алгебраическая дробь определена, называют областью определения данной дроби. Область определения для алгебраической дроби с несколькими переменными задавать сложно. Поэтому мы будем рассматривать области определения только для алгебраических дробей с одной переменной, например, с переменной Задавая алгебраическую дробь, иногда указывают и ее область определения. Пример 4. Дробь Пример 5. Если нас интересуют значения дроби Пример 6. Дробь Часто область определения алгебраической дроби Пример 7. Записывая дробь Пример 8. Записывая дробь 5.** Зависимость области определения дроби от числового множества. Область определения алгебраической дроби зависит от числового множества, в котором рассматриваются значения переменной. Пример 9. Дробь Пример 10. Дробь Пример 11. Дробь Еще раз обратим внимание, что когда область определения дроби 6. Основное свойство алгебраической дроби Рассмотрим числовую дробь Аналогичное свойство выполнено и для алгебраических дробей. Оно называется основным свойством алгебраической дроби. Значение алгебраической дроби не изменится, если числитель и знаменатель дроби умножить на один и тот же множитель, значение которого отлично от нуля. Иногда основное свойство алгебраической дроби формулируют по-другому: алгебраическая дробь не изменится, если числитель и знаменатель дроби умножить на один и тот же множитель, не обращающийся в нуль в области определения данной алгебраической дроби. При этом подразумевается, что значения дроби 7. Сокращение алгебраической дроби. Рассмотрим дроби при Перепишем равенство в виде Правая часть этого равенства получается из левой части сокращением числителя и знаменателя на один и тот же множитель При сокращении числителя и знаменателя на общий множитель часто получается дробь с меньшими степенями числителя и знаменателя. Пример 14. В этом примере мы сократили дробь на числовой множиПоэтому области определения дробей Пример 15. В этом примере мы сократили дробь на множитель Пример 16. Это равенство выполняется только при таких значениях 8.** Тождественное равенство дробей на некотором множестве. Свойства рефлексивности, симметричности, транзитивности. Использование знака равенства при действиях с алгебраическими дробями имеет более сложный смысл, чем при действиях с многочленами. Чтобы в этом разобраться, определим тождественное равенство двух алгебраических дробей от переменной Алгебраические дроби Тождественное равенство дробей Тождественное равенство алгебраических дробей от переменной Свойство 1. Пусть дробь Свойство 2. Пусть Свойство 3. Пусть Пример 17. При 1. Что такое целое алгебраическое выражение? 2. Что такое алгебраическая дробь? 3. Дайте определение числителя и знаменателя алгебраической дроби. 4. При каких значениях переменных алгебраическая дробь не определена? 5. Каким условиям должна удовлетворять область определения алгебраической дроби? 6. Как находить область определения алгебраической дроби в том случае, когда эта область не указана? 7. Сформулируйте основное свойство алгебраической дроби. 8. Что называют сокращением алгебраической дроби? 9. Что нужно сделать, чтобы сократить алгебраическую дробь, если это возможно? Задачи и упражнения 1. При каких значениях переменной определена алгебраическая дробь: а) г) 2. Сократите алгебраическую дробь: а) д) 3. Укажите, при каких значениях переменных исходная дробь равна той дроби, которая получается после сокращения. Сократите алгебраическую дробь: а) г) 4. Сократите алгебраическую дробь: а) г) Ответы и указания к решению наиболее трудных задач. Задача 4. Указание. а) б) в) Если г) д) е)
|
|---|













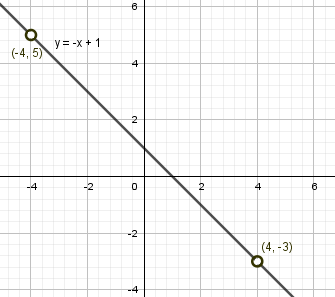







 Получаем два числовых
Получаем два числовых 


 ,
,  ,
,  ,
,  ,
,  .
. при
при  и
и  имеет значение, равное
имеет значение, равное  .
.
 имеет знаменатель
имеет знаменатель  , который обращается в нуль при
, который обращается в нуль при  . Поэтому данная дробь не определена при
. Поэтому данная дробь не определена при  имеет знаменатель
имеет знаменатель  , который тождественно равен нулю. Поэтому данная дробь не определена ни при каком значении
, который тождественно равен нулю. Поэтому данная дробь не определена ни при каком значении  .
. имеет знаменатель
имеет знаменатель  , который обращается в нуль при
, который обращается в нуль при  . Поэтому данная дробь не определена, если брать равные значения переменных
. Поэтому данная дробь не определена, если брать равные значения переменных  и
и  .
. . В этом случае дробь имеет вид
. В этом случае дробь имеет вид  , где
, где  и
и  — многочлены.
— многочлены. рассматривается при всех действительных
рассматривается при всех действительных 
 для положительных
для положительных  .
. рассматривается при всех натуральных
рассматривается при всех натуральных  . В данном примере область определения дроби — это множество всех натуральных чисел.
. В данном примере область определения дроби — это множество всех натуральных чисел. .
. .
. всюду определена, если рассматриваются только натуральные значения переменной
всюду определена, если рассматриваются только натуральные значения переменной  дробь не определена.
дробь не определена. всюду определена, если рассматривать только целые значения переменной
всюду определена, если рассматривать только целые значения переменной  . И эта же дробь не всюду определена, если рассматривать рациональные значения
. И эта же дробь не всюду определена, если рассматривать рациональные значения  дробь не определена.
дробь не определена. всюду определена, если рассматривать только рациональные значения переменной
всюду определена, если рассматривать только рациональные значения переменной  и при
и при  дробь не определена.
дробь не определена. . Значение этой дроби не изменится, если мы умножим числитель и знаменатель на одно и то же не равное нулю число. Например,
. Значение этой дроби не изменится, если мы умножим числитель и знаменатель на одно и то же не равное нулю число. Например,

 рассматриваются на общей части их областей определения.
рассматриваются на общей части их областей определения. и
и  . По основному свойству дробей эти дроби равны на общей части их областей определения, то есть
. По основному свойству дробей эти дроби равны на общей части их областей определения, то есть
 .
.
 . Будем говорить, что дробь
. Будем говорить, что дробь  получается из дроби
получается из дроби  .
. и
и  одинаковы, и равенство
одинаковы, и равенство  выполняется при любом
выполняется при любом  .
. .
. . Однако, левая дробь не определена ни при каком значении
. Однако, левая дробь не определена ни при каком значении  .
. и
и  , при которых определены как первая, так и последняя дроби, то есть
, при которых определены как первая, так и последняя дроби, то есть  и
и  .
. чисел.
чисел. тождественно равны на множестве
тождественно равны на множестве  значения
значения  определены и равны.
определены и равны. , вместо которого иногда используют обычный знак равенства, когда из текста ясно, что речь идет о тождественном равенстве алгебраических дробей на некотором множестве.
, вместо которого иногда используют обычный знак равенства, когда из текста ясно, что речь идет о тождественном равенстве алгебраических дробей на некотором множестве. на множестве
на множестве  на множестве
на множестве  на множестве
на множестве  на множестве
на множестве  . Тогда
. Тогда  на пересечении множеств
на пересечении множеств  имеем равенство
имеем равенство  .
. ,
,  . Поэтому на основании свойства 3 при
. Поэтому на основании свойства 3 при 
 б) ;
б) ;  в) ;
в) ;  ;
; д) ;
д) ;  е) ;
е) ;  ж) ;
ж) ;  ?
? б) ;
б) ;  в) ;
в) ;  г) ;
г) ;  ;
; е) ;
е) ;  ж) ;
ж) ;  .
. б) ;
б) ;  в) ;
в) ;  ;
; д) ;
д) ;  е) ;
е) ;  ж) ;
ж) ;  .
. б) ;
б) ;  в) ;
в) ;  ;
; д) ;
д) ;  е) ;
е) ;  .
. ,
, 
 .
. ,
, 
 .
. , то рассматриваемая дробь не имеет смысла, поэтому
, то рассматриваемая дробь не имеет смысла, поэтому  . Сократив числитель и знаменатель на
. Сократив числитель и знаменатель на  и приведя подобные члены получим выражение
и приведя подобные члены получим выражение  . Если ввести новую переменную
. Если ввести новую переменную  , то в результате получим алгебраическую дробь вида
, то в результате получим алгебраическую дробь вида  . Корнями уравнения
. Корнями уравнения  являются числа
являются числа  и
и  , поэтому
, поэтому  . Так что сократить можно только на числовой множитель.
. Так что сократить можно только на числовой множитель.
 при всех
при всех  .
.
 при всех
при всех  и
и  таких, что
таких, что  и
и  .
.
 при всех таких
при всех таких  , что
, что  и
и  .
.