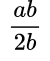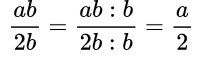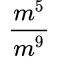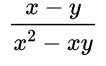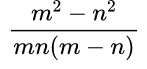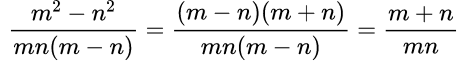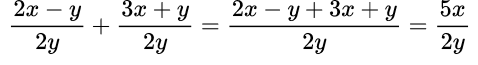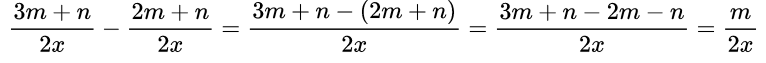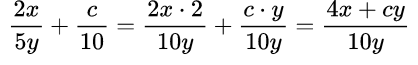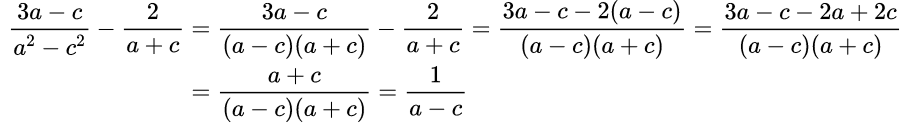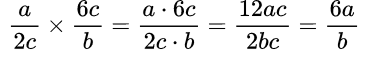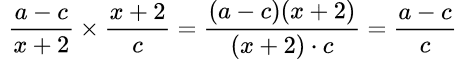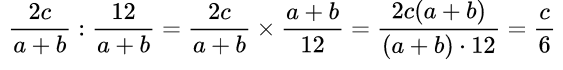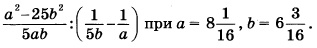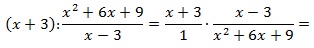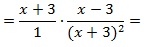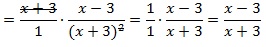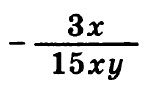Значение алгебраической дроби определено при условии что
Понятие алгебраической дроби. Основное свойство
Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
Алгоритм приведения алгебраических дробей к общему знаменателю
Шаг 2. Дополнительные множители
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
Дробь также не изменится, если провести следующие перемены знаков:
Ещё несколько полезных формул, связанных с переменой знаков:
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
$ a^2-4 \neq 0 \iff (a-2)(a+2) \neq 0 \iff a \neq \pm 2$
$ 3x-1 \neq 0 \iff x \neq \frac<1><3>$
$$ x- \frac<4>
$ y^2-3|y| \neq 0 \iff |y|(|y|-3) \neq 0 \iff <\left\< \begin
Пример 2. Сократите дроби:
Пример 3. Упростите выражение:
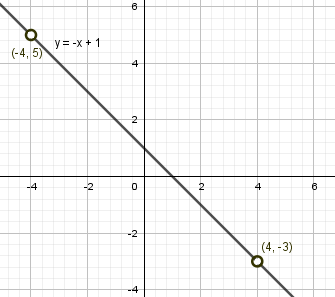
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
Область определения функции
Прежде чем перейти к изучению области определения функции внимательно изучите уроки
«Что такое функция в математике» и «Как решать задачи на функцию».
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
Вместо « x » (аргумента функции) в формулу « у = 2x » подставляем произвольные числовые значения и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу « у = 2x » и запишем результаты в таблицу.
| x | y = 2 x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
| y = 2 ·
=
= 1 | ||||||
| x = 3 | y = 2 · 3 = 6 |
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
Вернемся к нашей функции « у = 2x » и найдем её область определения.
Посмотрим ещё раз на таблицу функции « y = 2x », где мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
| 1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать, что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
В нашей функции « у = 2x » вместо « x » можно подставить любое число, поэтому область определения функции « у = 2x » — это любые действительные числа.
Запишем область определения функции « у = 2x » через математические обозначения.
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на математические символы. Для этого вспомним понятие числовой оси.
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции « у = 2x ». Так как в функции
« у = 2x » нет ограничений для « x », заштрихуем всю числовую ось от минус бесконечности « −∞ » до плюс бесконечности « +∞ ».
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как « x ∈ R ».
Читается « x ∈ R » как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
« x ∈ R » одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
№ 233 (2) Мерзляк 8 класс
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x » в функции
« f(x) =
| 8 |
| x + 5 |
».
По законам математики из школьного курса мы помним, что на ноль делить нельзя. Иначе говоря, знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции « f(x) =
| 8 |
| x + 5 |
». Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
Получается, что « x » может принимать любые числовые значения кроме « −5 ». На числовой оси заштрихуем все доступные значения для « x ».
Число « −5 » отмечено «пустой» точкой на числовой оси, так как не входит в область допустимых значений.
Запишем заштрихованную область на числовой оси через знаки неравенства.
Запишем промежутки через математические символы. Так как число « −5 » не входит в область определения функции, при записи ответа рядом с ним будет стоять круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке «Как записать ответ неравенства».
Запишем окончательный ответ для области определения функции
« f(x) =
| 8 |
| x + 5 |
».
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
№ 98 (5) Колягин (Алимов) 8 класс
Найти область определения функции:
Из урока «Квадратный корень» мы помним, что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
« у = √ 6 − x ». Подкоренное выражение
« 6 − x » должно быть больше или равно нулю.
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
Запишем полученный ответ, используя числовую ось и математические символы. Число « 6 » отмечено «заполненной» точкой на числовой оси, так как входит в область допустимых значений.
Правило для определения области определения функции
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
№ 242 (3) Мерзляк 8 класс
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции « f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» есть дробь «
| 1 |
| x 2 − 9 |
», где « x » расположен в знаменателе. Запишем условие, что знаменатель « x 2 − 9 » не может быть равен нулю.
Решаем квадратное уравнение через формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −0 ± √ 0 2 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
| −0 ± √ 0 − (−36) |
| 2 |
Запомним полученный результат. Задаем себе второй вопрос. Проверяем, есть ли в формуле функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
» корень четной степени. В формуле есть квадратный корень « √ x + 3 ». Подкоренное выражение « x + 3 » должно быть больше или равно нулю.
Решим линейное неравенство.
Объединим полученные ответы по обоим вопросам:
Объединим все полученные результаты на числовых осях. Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях. Обратим внимание, что числа « −3 » и « 3 » отмечены «пустыми» точками и не входят в итоговое решение.

промежутка « −3 » и « x > 3 », которые являются областью определения функции
« f(x) = √ x + 3 +
| 1 |
| x 2 − 9 |
». Запишем окончательный ответ.
Примеры определения области определения функции
№ 101 Колягин (Алимов) 8 класс
Найти область определения функции:
Для поиска области определения функций задаем себе первый вопрос. Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
« y = 6 √ x + 5 √ 1 + x » нет дробей.
Задаем второй вопрос. Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени: « 6 √ x ». Степень корня — число « 6 ». Число « 6 » — чётное, поэтому подкоренное выражение корня « 6 √ x » должно быть больше или равно нулю.
В формуле функции « y = 6 √ x + 5 √ 1 + x » также есть корень пятой степени
« 5 √ 1 + x ». Степень корня « 5 » — нечётное число, значит, никаких ограничений на подкоренное выражение « 1 + x » не накладывается.
Получается, что единственное ограничение области определения функции
« y = 6 √ x + 5 √ 1 + x » — это ограничение подкоренного выражения « 6 √ x ».
Нарисуем область определения функции на числовой оси и запишем ответ.
№ 242 (4) Мерзляк 8 класс
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два. Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √ x + 2 ≠ 0 |
| x 2 − 7x + 6 ≠ 0 |
Обозначим их номерами « 1 » и « 2 » и решим каждое уравнение отдельно.
| √ x + 2 ≠ 0 (1) |
| x 2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
Если значение квадратного корня
« √ x + 2 ≠ 0 » не должно быть равно нулю, значит, подкоренное выражение
« x + 2 ≠ 0 » также не должно быть равно нулю.
Теперь решим уравнение под номером « 2 », используя формулу квадратного уравнения.
x1;2 =
| −b ± √ b 2 − 4ac |
| 2a |
x1;2 =
| −(−7) ± √ (−7) 2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
| 7 ± √ 49 − 24 |
| 2 |
x1;2 =
| 7 ± 5 |
| 2 |
x1 ≠
| x2 ≠
|
x1 ≠
| x2 ≠
|
| x1 ≠ 6 | x2 ≠ 1 |
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
| x ≠ −2 |
| x ≠ 1 |
| x ≠ 6 |
В формуле функции
« f(x) =
| √ x − 4 |
| √ x + 2 |
+
| 4x − 3 |
| x 2 − 7x + 6 |
»
есть два корня « √ x − 4 » и « √ x + 2 ». Их подкоренные выражения должны быть больше или равны нулю.
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x − 4 ≥ 0 |
| x + 2 ≥ 0 |
| x ≥ 4 |
| x ≥ −2 |
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
Выпишем результат решения системы неравенств.
Объединим в таблицу ниже полученные ответы по обеим проверкам:
Результат проверки, что знаменатели дробей с « x » не равны нулю
Результат проверки, что подкоренные выражения должно быть больше или равны нулю
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет всем полученным условиям.
Алгебраические дроби
теория по математике 📈 алгебраические выражения
Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.
Примеры алгебраических дробей:
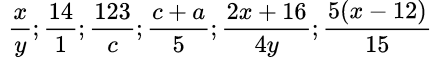
Сокращение алгебраической дроби
Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.
Пример №1. Сократим дробь:
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь:
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :
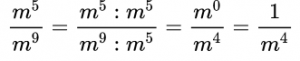
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
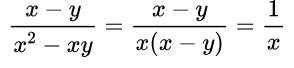
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).
Пример №5. Выполним сложение дробей:
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей:
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:
Пример №7. Выполнить сложение дробей:
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей:
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.
Пример №9. Выполнить умножение дробей:
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей:
Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.
Пример №11. Выполнить деление дробей:
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
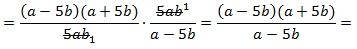


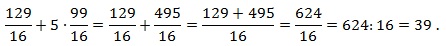
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
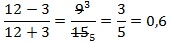
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить