Значение первого закона ньютона в чем состоит

Основные сведения о первом законе Ньютона

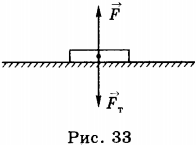
Явление инерции. Первый закон Ньютона

Инерция — это возможность тела сохранять свою скорость по величине и по направлению, при отсутствии каких-либо воздействий на тело.

Инертность — это свойство тела оставаться в покое или прямолинейно и равномерно двигаться.

Обычно первый закон Ньютона еще называют законом инерции.

В первом законе Ньютона говорится, что тела движутся прямолинейно и равномерно в существующих инерциальных системах отсчета, если на них не влияют никакие силы или действие других сил взаимно скомпенсировано.

Если сформулировать первый закон Ньютона проще, то получается следующее: если мы на ровной дороге толкнем машину и не будем учитывать сопротивление воздуха и силу трения колес, то она будет катиться бесконечно долго с одинаковой скоростью.

Но мы знаем, что на самом деле такого не существует. Абсолютно на все тела всегда действуют какие-либо силы, причем уравновесить действие этих сил целиком практически невозможно.

Основные положения, физический смысл

Физический смысл первого закона Ньютона заключается в том, что всякое тело сохраняет состояние покоя или прямолинейного и равномерного движения, пока сила или влияние со стороны других тел не заставят его поменять это состояние.

Особенности первого закона Ньютона

Особенность первого закона Ньютона заключается в том, что закон указывает на существование инерциальных систем отсчета, где равнодействующая всех сил равна нулю.

Если существует одна инерциальная система отсчета, то любая другая система, которая двигается относительно нее равномерно и прямолинейно, также будет являться инерциальной.

Примеры решения задач

Найти силу реакции опоры N, если кирпич массой 1,6 кг лежит на горизонтальном столе.

Уравнение первого закона Ньютона

Рассчитайте силу реакции опоры N, которая действует на нижний кирпич, если два кирпича массой 2 кг лежат один на другом на горизонтальной поверхности.

Найти силу натяжения нити T в месте крепления к потолку, если два шарика подвешены к нити. Каждый шарик имеет массу по 0,1 кг.

Ответ: масса шара равна 0,4 кг.

m = 2 к г g = 10 м / с 2 F = 12 H F т я ж = m g F + F т я ж = N N = F + m g N = 12 + 2 · 10 = 32 H

Источник

Самое важное значение законов Ньютона

ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА

Опыты и наблюдения показывают, что причиной изменения движения тел, т. е. причиной изменения их скорости, являются воздействия на них других тел. Количественно действие одного тела на другое, вызывающее изменение скорости, выражается величиной, называемой силой.

Действие одного тела на другое не одностороннее. Тела взаи­модействуют. Ускорение, которое получает тело при данном взаимодействии, зависит от особого свойства всякого тела — его инертности. Количественно это свойство выражается вели­чиной, называемой массой.

Эти опытные факты лежат в основе трех законов движения (динамики), открытых И. Ньютоном и изложенных им в книге «Математические начала натуральной философии», опубликован­ной в 1687 г. Эти законы имеют простую и краткую формули­ровку, если движения тел рассматриваются относительно над­лежащим образом выбранных систем отсчета — инерциальных систем.

Первый закон Ньютона утверждает, что относительно инер­циальных систем отсчета тело движется прямолинейно и равно­мерно или находится в покое, если сумма сил, действующих на него, равна нулю. Другими словами, в этом случае тело нахо­дится в состоянии равновесия. Вывести тело из состояния рав­новесия может только приложенная к нему сила. Математически первый закон Ньютона можно выразить так:

Если то

(— означает сумму).

Второй закон Ньютона устанавливает связь силы с вызван­ным ею ускорением: сила, действующая на тело независимо от ее природы, равна произведению массы тела на сообщаемое этой силой ускорение:

Третий закон Ньютона указывает на то, что действие одного тела на другое имеет взаимный характер: тела действуют друг на друга силами одной и той же природы, равными по модулю и противоположными по направлению:

Законы движения выражаются тремя простыми (на первый взгляд) формулами. Но содержится в них необыкновенно много. Ведь вокруг нас происходят самые разнообразные движения: течет вода в реках, низвергаются водопады, проносятся над Землей ветры и ураганы, мчатся по дорогам автомобили, пла­вают по морям корабли, летают в воздухе самолеты, в космиче­ском пространстве движутся галактики, звезды, планеты и создан­ные человеком космические корабли.

Эти движения и тела, ко­торые их совершают, не похожи одно на другое. Различны и силы, действующие на них. Но для всех этих движений, тел и сил справедливы законы Ньютона, математически выраженные в приведенных выше формулах, на вид таких простых.

Механика Ньютона была первой в истории физики (да и вообще науки) законченной теорией, правильно описывающей обширный класс явлений — движения тел. Один из современ­ников Ньютона так выразил свое восхищение этой теорией в стихах, которые мы приводим в вольном переводе :

Был этот мир глубокой тьмой окутан.

Да будет свет! И вот явился Ньютон.

Законы Ньютона в принципе позволяют решить любую задачу механики. Если известны силы, приложенные к телу, можно найти ускорение тела в любой момент времени, в любой точке его траектории.

Итак, получается такая «цепочка»:

По известным силам и массе тела находят ускорение, затем вычисляют его скорость, перемещение и, наконец, координаты тела в любой момент времени. Для этого нужно еще знать начальные условия — начальное положение и начальную скорость тела.

Законы Ньютона позволяют людям не только изучать движения, но и управлять ими. Например, ученым, которые управляют полетом космического корабля, необходимо, конечно, знать положение корабля в любой момент времени. Они и узнают его, пользуясь упоминавшейся «цепочкой». Им известно начальное положение корабля на стартовой площадке и его начальная скорость. Им известны и силы, действующие на корабль в любой точке его траектории. Пользуясь этими данными, они и решают задачу механики применительно к космическому кораблю. Но сил, действующих на корабль, много, они все время изменяются, а вычислять нужно не одну координату, а три. По этому вычисления настолько сложны, что приходится привлекать на помощь вычислительные машины.

Не следует думать, что законами механики пользуются исключительно для того, чтобы вычислять координаты движущихся тел. Нередки случаи, когда движение тела известно, т. е. из­вестно его положение в различные моменты времени. Тогда законы Ньютона позволяют выяснить, какие силы действуют на тело.

Источник

Законы Ньютона

Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.

Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».

Что такое сила

Тела действуют друг на друга с помощью сил.

Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.

Смысл законов Ньютона

Ньютон, в своих законах динамики, хотел сказать следующее:

Примечание:

Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».

Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).

Первый закон Ньютона

Словесная формулировка первого закона Ньютона:

В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).

Формула:

\( F = 0 \) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);

\( a = 0 \) – ускорение отсутствует;

\( v = const \) – скорость тела не изменяется (остается одной и той же);

\( p = const \) – импульс тела не изменяется (остается одним и тем же);

Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.

Значит, если на тело не действуют другие тела (силы), то

Второй закон Ньютона

Сформулируем словами второй закон Ньютона:

Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.

Формула второго закона Ньютона с пояснениями

\( a \left( \frac<\text<м>>> \right) \) – ускорение тела

\( m \left( \text <кг>\right) \) – масса тела

\( F \left( H \right) \) – сила, которую приложили к телу

Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет \( \vec < a >= 0 \)

Ускорение прямо пропорционально силе:

Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.

Ускорение обратно пропорционально массе:

Чем больше месса тела, тем труднее изменить его скорость.

Формулу второго закона часто записывают в векторном виде:

Мы можем заменить местами правую и левую части, в таком случае получим:

Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».

Дробь \( \displaystyle \frac<1> \) – это скалярная величина.

Примечания:

Третий закон Ньютона

Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.

Словами третий закона Ньютона можно сформулировать так:

Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.

\( F_ <12>\left( H \right) \) – сила, с которой первое тело действует на второе тело.

\( F_ <21>\left( H \right) \) – сила, с которой второе тело отвечает первому.

Пояснить формулу можно с помощью такого рисунка:

Обратите внимание, что длины красного и черного векторов равны.

Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:

Примечания:

Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:

Источник

Первый закон Ньютона.

Ньютон сформулировал закон инерции, включив его в основу механики в качестве первого из трех законов. Поэтому этот закон называют первым законом Ньютона.

Первый закон механики, или закон инерции был сформулирован Ньютоном следующим образом:

Любое тело удерживается в состоянии покоя или равномерного прямолинейного движения, пока под действием приложенных сил не изменяет это состояние.

В окружении любого тела, покоится оно или движется, есть другие тела, некоторые из которых или все как-то действуют на тело, влияют на состояние его движения. Чтобы выяснить влияние окружающих тел, надо исследовать каждый отдельный случай.

Рассмотрим какое-либо покоящееся тело, не обладающее ускорением, а скорость постоянна и равна нулю. Допустим, это будет шарик, подвешенный на резиновом шнуре. Он находится в покое относительно Земли. Около шарика множество различных тел: шнур, на котором он висит, множество предметов в комнате и других помещениях и, конечно, Земля. Однако, действие всех этих тел на шарик не одинаково. Если, например, убрать мебель в комнате, это не окажет какого-либо влияния на шарик. Но если перерезать шнур, шарик под влиянием Земли начнет падать вниз с ускорением. Но пока шнур не был перерезан, шарик находился в покое. Этот простой опыт показывает, что из всех тел, окружающих шарик, только два заметно влияют на него: резиновый шнур и Земля. Их совместное влияние и обеспечивает состояние покоя шарика. Стоило устранить одно из этих тел — шнур, и состояние покоя нарушилось. Если бы возможно было убрать Землю, это тоже нарушило бы покой шарика: он стал бы двигаться в противоположном направлении.

Отсюда приходим к выводу, что действия на шарик двух тел — шнура и Земли, компенсируют (уравновешивают) друг друга. Когда говорят, что действия двух или нескольких тел компенсируют друг друга, то это значит, что результат их совместного действия такой же, как если бы этих тел вовсе не было.

Рассмотренный пример, как и другие подобные примеры, позволяют сделать следующий вывод: если действия тел компенсируют друг друга, то тело под влиянием этих тел находится в состоянии покоя.

Таким образом, мы пришли к одному из основных законов механики, который называют первым законом Ньютона:

Существуют такие системы отсчета, относительно которых движущиеся тела сохраняют свою скорость постоянной, если на них не действуют другие тела или действие других тел компенсируется.

Однако, как выяснилось со временем, первый закон Ньютона выполняется только в инерциальных системах отсчета. Поэтому с точки зрения современных представлений закон Ньютона формулируют следующим образом:

Системы отсчета, относительно которых свободное тело при компенсации внешних воздействий движется равномерно и прямолинейно, называют инерциальными системами отсчета.

Свободным телом в этом случае называют тело, на которое другие тела не оказывают воздействия.

Необходимо помнить, что в первом законе Ньютона рассматриваются тела, которые могут быть представлены в качестве материальных точек.

Источник

Законы Ньютона

1. В основе классической механики лежат три закона Ньютона, которые были сформулированы им при обобщении результатов наблюдений и опытов в конце XVII в.

Первый закон, включённый Ньютоном в систему законов, был открыт Галилеем и назван им законом инерции. Закон инерции формулируется следующим образом: если на тело не действуют другие тела, то оно либо находится в покое, либо движется равномерно прямолинейно.

2. В природе не существует отдельных изолированных тел. Любое тело взаимодействует с окружающими телами. Несмотря на это, взаимодействующие тела могут находиться в покое или двигаться равномерно и прямолинейно.

3. При компенсации действия на тело других тел оно может двигаться равномерно прямолинейно.

Например, если по прямой горизонтальной дороге движется автомобиль, то при компенсации действия на него силы тяги двигателя и силы трения со стороны поверхности дороги движение автомобиля будет равномерным.

Можно утверждать, что тело сохраняет состояние покоя, если действие на него других тел скомпенсировано.

Явление сохранения скорости тела постоянной (в том числе и равной нулю) называют явлением инерции.

4. Тело сохраняет состояние покоя или равномерного прямолинейного движения, если на него не действуют другие тела или действие других тел скомпенсировано не во всех системах отсчёта, а только в инерциальных системах отсчёта.

Инерциальными системами отсчёта называются такие системы отсчёта, относительно которых поступательно движущееся тело сохраняет свою скорость постоянной, если на него не действуют другие тела или действия других тел компенсируются. Инерциальной можно считать систему отсчёта, связанную с Землёй. Системы отсчёта, движущиеся относительно Земли равномерно и прямолинейно, также являются инерциальными.

Системы отсчёта, движущиеся с ускорением относительно инерциальной системы отсчёта, например относительно Земли, называют неинерциальными.

5. Значение первого закона Ньютона состоит в том, что он устанавливает существование инерциальных систем отсчёта (таких систем отсчёта, относительно которых тела движутся с постоянной скоростью при компенсации внешних воздействий). Именно для таких систем отсчёта справедливы все другие законы Ньютона.

6. Второй закон Ньютона устанавливает зависимость ускорения одного из взаимодействующих тел от его массы и действующей на него силы. Наблюдения и опыты свидетельствуют о том, что чем больше сила, действующая на тело, тем больше ускорение, которое оно приобретает. Так, чем сильнее водитель нажимает на педаль тормоза, тем
больше сила и тем быстрее автомобиль остановится. Значит, чем больше действующая на автомобиль сила сопротивления, тем больше его ускорение.

Ускорение, которое приобретают тела под действием одинаковой силы, зависит от массы тел. Например, грузовому автомобилю требуется большее время, чем легковому, для того, чтобы, имея некоторую одинаковую скорость, остановиться, выключив двигатель. Из этого примера следует, что чем больше масса тела, тем меньшее ускорение оно получает под действием некоторой постоянной силы.

7. Второй закон Ньютона формулируется следующим образом: ускорение, с которым движется тело прямо пропорционально действующей на тело силе и обратно пропорционально массе тела.

Записанное равенство представляет собой второй закон Ньютона.

В механике Ньютона ускорение тел обусловлено только их взаимодействием. Следовательно, второй закон Ньютона справедлив в инерциальных системах отсчёта.

8. Действие тел друг на друга носит взаимный характер, т.е. в результате взаимодействия
каждое тело приобретает ускорение, и, следовательно, на каждое из взаимодействующих тел действует сила. Например, груз, висящий на нити, действует на нить с силой, направленной вертикально вниз \( (\vec_1) \) ​, и растягивает её (рис. 34). В свою очередь, нить действует на груз с силой, направленной вертикально вверх \( (\vec_2) \) ​.

9. Измерения показывают, что:

10. Из соотношения следует: ​ \( m_1a_1=m_2a_2 \) ​.

Поскольку ускорение — величина векторная и ускорения, которые получают тела, направлены в противоположные стороны, то ​ \( m_1\vec_1=-m_2\vec_2 \) ​.

Это равенство и выражает третий закон Ньютона.

Третий закон Ньютона формулируется следующим образом: тела действуют друг на друга с силами, равными по модулю и направленными в противоположные стороны. Эти силы направлены вдоль прямой, соединяющей взаимодействующие тела (материальные точки).

Третий закон Ньютона говорит о том, что силы всегда проявляются парами.

Эти силы часто называют силами действия и противодействия. При этом безразлично, какую из двух сил назвать силой действия, а какую — силой противодействия.

Эти силы приложены к разным телам, и их нельзя складывать, т.е. нельзя сказать, что силы действия и противодействия уравновешивают друг друга.

Силы, с которыми взаимодействуют тела, всегда одной природы.

Третий закон Ньютона, так же как первый и второй законы, справедлив в инерциальных системах отсчёта.

10. При переходе от одной инерциальной системы отсчёта к другой не изменяются ни ускорение, ни масса тала, ни действующая на него сила. Следовательно, можно утверждать, что законы механики одинаковы для всех инерциальных систем отсчёта, или, что то же самое, все механические явления протекают одинаково во всех инерциальных системах отсчёта при одинаковых начальных условиях. Это утверждение называется принципом относительности Галилея.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Утверждение, что материальная точка покоится или движется равномерно прямолинейно, если на неё не действуют другие тела или действие на неё других тел взаимно уравновешено,

1) неверно ни для каких систем отсчёта
2) верно для инерциальных систем отсчёта
3) верно для неинерциальных систем отсчёта
4) верно при любых условиях

2. Система отсчёта, связанная с Землёй, может считаться инерциальной. Система отсчёта, связанная с автобусом, тоже будет инерциальной, если он

1) движется равномерно по извилистой дороге
2) тормозит у остановки
3) отъезжает от светофора
4) движется равномерно по прямолинейному участку пути

3. В каком из приведённых примеров тело движется по инерции:

1) равномерно движущийся по горизонтальной дороге автомобиль
2) автомобиль, движущийся по горизонтальной дороге с выключенным двигателем
3) автомобиль, поворачивающий направо
4) автомобиль, выезжающий со стоянки

4. Яблоко, лежащее неподвижно на столе вагона движущегося поезда покатился вправо, если смотреть по ходу поезда. Как изменилось движение поезда?

1) скорость поезда увеличилась
2) скорость поезда уменьшилась
3) поезд повернул влево
4) поезд повернул вправо

5. Можно ли считать инерциальной системой отсчёта движущийся автомобиль?

1) можно всегда
2) можно, только если он движется равномерно и прямолинейно
3) можно только во время разгона и торможения
4) нельзя ни при каких условиях

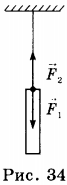
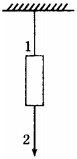
6. Массивный груз подвешен на тонкой нити 1. К грузу прикреплена такая же нить 2. Если
медленно тянуть за нить 2, то оборвётся

1) только нить 1
2) только нить 2
3) нить 1 и нить 2 одновременно
4) либо нить 1, либо нить 2, в зависимости от массы груза

7. Нить, привязанная одним концом к вбитому в стену гвоздю, разорвётся, если другой её конец тянуть с силой не менее 50 Н. Чему равно наименьшее значение сил, с которыми растягивают эту же нить за оба конца, при котором она рвётся?

1) 25 Н
2) 50 Н
3) 75 Н
4) 100 Н

8. Два ученика тянут динамометр в противоположные стороны с силой 60 Н каждый. Каково показание динамометра?

1) 0 Н
2) 30 Н
3) 60 Н
4) 120 Н

1) ​ \( F_2 = 0 \) ​
2) ​ \( F_1=F_2 \) ​
3) \( F_1>F_2 \)
4) \( F_1

1) 1,5 т
2) 7,5 т
3) 15 т
4) 75 т

11. Из приведенных утверждений выберите два правильных и запишите их номера в таблицу.

1) законы Ньютона справедливы во всех системах отсчета
2) первый закон Ньютона утверждает существование инерциальных систем отсчета
3) равнодействующая сил действия и противодействия равна нулю
4) силы действия и противодействия имеют одинаковую природу
5) второй закон Ньютона говорит о том, что масса тела прямо пропорциональна действующей на тело силе

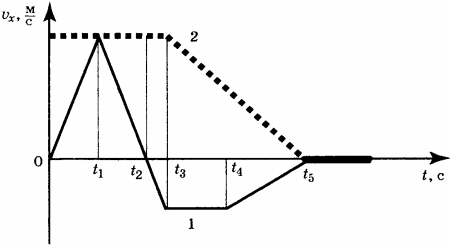
12. Два тела движутся по оси ​ \( Ox \) ​. На рисунке представлены графики зависимости проекции скорости движения тел 1 и 2 от времени.

Используя данные графика, выберите из предложенного перечня два верных утверждения. Укажите их номера.

1) В промежутке времени ​ \( t_3-t_5 \) ​ на тело 2 действует постоянная сила.
2) В промежутке времени ​ \( 0-t_3 \) ​ сила сообщает телу 1 положительное ускорение
3) В промежутке времени ​ \( t_4-t_5 \) ​ на тело 1 сила не действует
4) Модуль силы, действующей на тело 1 в промежутки времени ​ \( 0-t_1 \) ​, ​ \( t_1-t_2 \) ​ различен.
5) В промежутке времени ​ \( t_1-t_2 \) ​ сила сообщает телу 1 отрицательное ускорение

Часть 2

13. Тело массой 7 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 4 с груз был поднят на высоту 16 м?

Источник