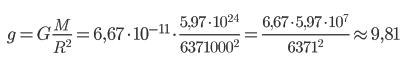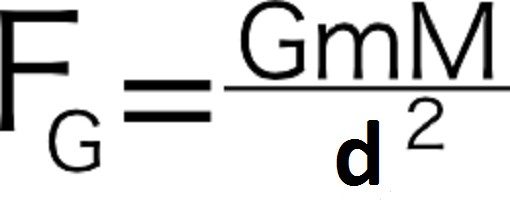Чему численно равно ускорение свободного падения
Ускорение свободного падения
Сила тяготения
В 1682 году Исаак Ньютон открыл закон всемирного тяготения. Он звучит так: все тела притягиваются друг к другу, сила всемирного тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними.
Формула силы тяготения согласно этому закону выглядит так:
Закон всемирного тяготения
F — сила тяготения [Н]
M — масса первого тела (часто планеты) [кг]
m — масса второго тела [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Когда мы встаем на весы, стрелка отклоняется. Это происходит потому, что масса Земли очень большая, и сила тяготения буквально придавливает нас к поверхности. На более легкой Луне человек весит меньше в шесть раз.
Закон всемирного тяготения используют, чтобы вычислить силы взаимодействия между телами любой формы, если размеры тел значительно меньше расстояния между ними.
Если мы возьмем два шара, то для них можно использовать этот закон вне зависимости от расстояния между ними. За расстояние R между телами в этом случае принимается расстояние между центрами шаров.
Приливы и отливы существуют благодаря закону всемирного тяготения. В этом видео я рассказываю, что общего у приливов и прыщей. 🤓
Ускорение свободного падения
Чтобы математически верно и красиво прийти к ускорению свободного падения, нам необходимо сначала ввести понятие силы тяжести.
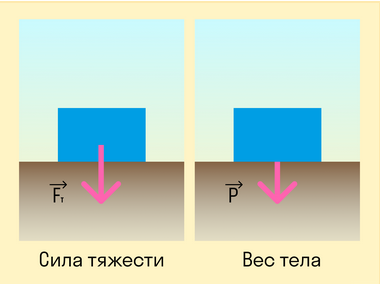
Сила тяжести — сила, с которой Земля притягивает все тела.
Сила тяжести
F = mg
F — сила тяжести [Н]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
На первый взгляд сила тяжести очень похожа на вес тела. Действительно, в состоянии покоя на поверхности Земли формулы силы тяжести и веса идентичны. Вес тела в состоянии покоя численно равен массе тела, умноженной на ускорение свободного падения, разница состоит лишь в точке приложения силы.
Сила тяжести — это сила, с которой Земля действует на тело, а вес — сила, с которой тело действует на опору. Это значит, что у них будут разные точки приложения: у силы тяжести к центру масс тела, а у веса — к опоре.
Также важно понимать, что сила тяжести зависит исключительно от массы и планеты, на которой тело находится. А вес зависит еще и от ускорения, с которым движется тело или опора.
Например, в лифте вес зависит от того, куда и с каким ускорением двигаются его пассажиры. А силе тяжести все равно, куда и что движется — она не зависит от внешних факторов.
На второй взгляд сила тяжести очень похожа на силу тяготения. В обоих случаях мы имеем дело с притяжением — значит, можем сказать, что это одно и то же. Практически.
Мы можем сказать, что это одно и то же, если речь идет о Земле и каком-то предмете, который к этой планете притягивается. Тогда мы можем даже приравнять эти силы и выразить формулу для ускорения свободного падения:
Приравниваем правые части:
Делим на массу левую и правую части:
Это и будет формула ускорения свободного падения. Ускорение свободного падения для каждой планеты уникально.
Формула ускорения свободного падения
g — ускорение свободного падения [м/с 2 ]
M — масса планеты [кг]
R — расстояние между телами [м]
G — гравитационная постоянная
Ускорение свободного падения характеризует то, как быстро увеличивается скорость тела при свободном падении.
Свободное падение — это ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести.
Ускорение свободного падения на разных планетах
Выше мы уже вывели формулу ускорения свободного падения. Давайте попробуем рассчитать ускорение свободного падения на планете Земля.
Для этого нам понадобятся следующие величины:
Подставим значения в формулу:
И кому же верить?
Ниже представлена таблица ускорений свободного падения и других характеристик для планет Солнечной системы, карликовых планет и Солнца.
Небесное тело
Ускорение свободного падения, м/с 2
Диаметр, км
Расстояние до Солнца, миллионы км
Масса, кг
Соотношение с массой Земли
Ускорение свободного падения
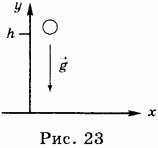
Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно \( R = \left( r + h \right) \), как представлено на рисунке 1.
Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).
Свободное падение – это движение тела под действием только одной силы — силы притяжения.
Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.
Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.
Формула для расчета ускорения свободного падения
Ускорение свободного падения можно посчитать по формуле:
\( g \left( \frac<\text<м>>
\( M \left( \text <кг>\right) \) (килограммы) — масса планеты, которая притягивает
\( r \left( \text <м>\right) \) (метры) – радиус планеты
\( h \left( \text <м>\right) \) (метры) — расстояние от поверхности планеты до тела
\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная
Интересные факты
У разных планет ускорение свободного падения различается.
Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.
Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.
В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.
Ускорение свободного падения у поверхности некоторых небесных тел
Как вывести формулу ускорения свободного падения
Рассмотрим камень, находящийся на некотором расстоянии от Земли.
Земля и камень притягиваются, запишем закон притяжения между планетой и камнем
С другой стороны, у камня есть вес, так как на него действует сила тяжести.
Мы можем записать эти уравнения в виде системы.
\[ \begin
Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:
А если равны левые части уравнений, то будут равны и правые:
Масса \( m \) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.
Ускорение свободного падения
| Солнце | 273,1 | ||
| Меркурий | 3,68—3,74 | Венера | 8,88 |
| Земля | 9,81 | Луна | 1,62 |
| Церера | 0,27 | Марс | 3,86 |
| Юпитер | 23,95 | Сатурн | 10,44 |
| Уран | 8,86 | Нептун | 11,09 |
| Плутон | 0,61 |
Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
где 

Содержание
Вычисление ускорения свободного падения
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центробежного ускорения.
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету однородным шаром массой M и вычислив гравитационное ускорение на расстоянии её радиуса R :


Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. Отличия обусловлены:
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
Перегрузки
Ускорение свободного падения: открытие, причины, формула
Ускорение свободного падения – одно из множества открытий великого Ньютона, который не только суммировал опыт предшественников, но и дал строгое математическое объяснение огромному количеству фактов и экспериментальных данных.
Предпосылки открытия. Эксперименты Галилея
Один из многочисленных экспериментов Галилео Галилея был посвящен исследованию движения тел в полете. До этого в системе мировоззрения господствовало мнение, что более легкие тела падают медленнее, чем тяжелые. Бросая различные предметы с высоты Пизанской башни, Галилей установил, что ускорение свободного падения для тел с различной массой абсолютно одинаково.
Теория Ньютона
Честь открытия закона всемирного тяготения принадлежит Ньютону, но сама идея уже около 200 лет витала в воздухе. Основной предпосылкой для формирования новых принципов небесной механики стали законы Кеплера, сформулированные им на основе многолетних наблюдений. Из океана допущений и домыслов Ньютон извлек предположение о силе притяжения Солнца и расширил свою теорию до понятия о всемирном тяготении. Он проверил свою гипотезу об обратной пропорциональности силы квадрату расстояния, рассмотрев орбиту Луны. Последующие проверки этой идеи осуществлялись при помощи исследования движения спутников Юпитера. Результаты наблюдений показали, что между спутниками планет и самими планетами действуют те же силы, что и при взаимодействии Солнца и планет.
Открытие гравитационной составляющей
Сила притяжения Земли к Солнцу подчинялась формуле:
Эксперименты показали, что множитель 1/d 2 в этом соотношении был вполне применим и в случае рассмотрения других планет в Солнечной системе. Постоянная G являлась коэффициентом, приводившим значение пропорции к числовой величине.
Руководствуясь собственной теорией, Ньютон измерил соотношения масс различных небесных тел, например масса Юпитера / масса Солнца, масса Луны / масса Земли, но численный ответ на вопрос о том, сколько весит Земля, Ньютон дать не мог, так как постоянная G по-прежнему оставалась неизвестной.
Величина гравитационной постоянной была открыта лишь спустя полвека после смерти Ньютона. Оценки этой величины на основе гипотез, подобных предположениям Ньютона, показали, что данная величина является ничтожно малой, и в земных условиях вычислить ее значение практически невозможно. Обычная сила тяжести кажется огромной, поскольку все знакомые нам предметы невообразимо малы по сравнению с массой земного шара.
Конец 18 века. Измерение G
Первые попытки измерить G состоялись в конце 18 века. В качестве притягивающей силы они использовали гору огромных размеров. Оценка величины ускорения свободного падения производилась на основании отклонения от вертикали грузика маятника, расположенного в непосредственной близости от горы. С помощью геологических данных была произведена оценка массы горы и ее среднее расстояние от маятника. Так получили первое, довольно грубое измерение загадочной константы.
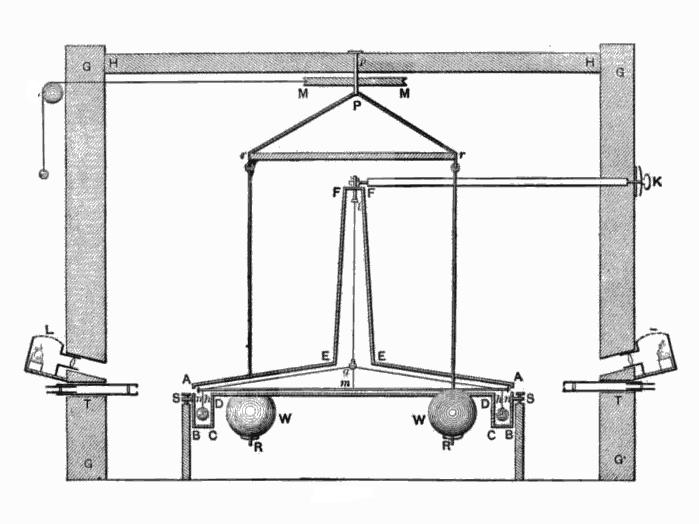
Измерения лорда Кавендиша
Лорд Кавендиш в своей лаборатории провел измерения гравитационного притяжения методом свободного взвешивания.
Вычислив силы закручивания нити, Кавендиш произвел оценку величины G, которая впоследствии была лишь немного откорректирована благодаря другим, более точным экспериментам. В современной системе единиц:
Данная величина является одной из немногочисленных физических констант. Ее значение неизменно в любой точке Вселенной.
Измерение ускорения Земли
Согласно третьему закону Ньютона сила притяжения двух тел зависит лишь от их массы и расстояния между ними. Таким образом, подставляя в правую часть уравнения множитель, известный из второго закона Ньютона, получаем:
В нашем случае массу m можно сократить, а величина а и есть ускорение, с которым тело m притягивается к Земле. В настоящее время ускорение свободного падения принято обозначать буквой g. Получаем:
Значения G для разных широт
Значение G для Луны
Наш спутник подчиняется тем же законам, что и остальные планеты Солнечной системы. Строго говоря, вычисляя ускорение на поверхности Луны, следует принимать во внимание и притяжение со стороны Солнца.
Именно такое малое значение GЛ является главной причиной того, что на Луне отсутствует атмосфера. По некоторым данным на заре времен наш спутник имел атмосферу, но из-за слабого притяжения Луна довольно быстро ее растеряла. Все планеты с большой массой обычно обладают собственной атмосферой. Ускорение свободного падения у них достаточно велико для того, чтобы не только не терять собственную атмосферу, но и прихватывать из космоса некоторое количество молекулярного газа.
Свободное падение
1. Свободное падение — падение тел в безвоздушном пространстве под действием притяжения к Земле. Наблюдения свидетельствуют о том, что скорость свободно падающего тела увеличивается с течением времени. Поскольку на свободно падающее тело действует единственная сила — сила тяжести, то его ускорение постоянно, т.е. свободное падение — движение равноускоренное.
2. Опыт показывает, что все свободно падающие тела движутся с одинаковым ускорением. Так, если вертикально расположенную трубку, в которой находятся три тела, имеющие разную массу: пёрышко, кусочек пробки и дробинку, перевернуть, то эти тела будут падать на дно трубки. При этом, если в трубке есть воздух, то из-за сопротивления воздуха они упадут не одновременно: дробинка упадёт раньше всех, а пёрышко позже всех тел. Если же воздух из трубки откачать, то тела упадут на дно одновременно.
Ускорение свободного падения зависит от высоты тела над поверхностью Земли. Чем выше поднято тело, тем слабее оно притягивается к Земле, тем меньше ускорение свободного падения.
4. Уравнения зависимости от времени модуля скорости, пути и модуля перемещения свободно падающего тела с высоты \( h \) (рис. 23).
Уравнения зависимости от времени проекции скорости и координаты свободно падающего тела с некоторой высоты тела:
Знаки проекций зависят от направления оси координат и начала координат. В соответствии с рисунком
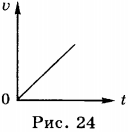
5. График зависимости модуля скорости от времени при свободном падении приведён на рисунке (рис. 24).
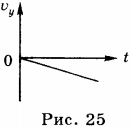
6. График зависимости проекции скорости от времени при свободном падении приведены на рисунке (ось Y направлена вертикально вверх) (рис. 25).
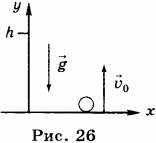
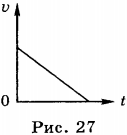
7. Тело, брошенное вертикально вверх, тоже движется равноускоренно с ускорением \( g \) , которое направлено вертикально вниз. В этом случае, в отличие от свободного падения, скорость и ускорение движения направлены в противоположные стороны (рис. 26).
8. Уравнения зависимости от времени модуля скорости, пути и модуля перемещения тела, брошенного вертикально вверх с начальной скоростью \( v_0 \) :
\[ v=v_0-gt; l=v_0t-gt^2/2; s=v_0t-gt^2/2 \]
Записанная формула зависимости пути от времени может быть использована только при движении тела в одну сторону (в данном случае вверх).
Уравнения зависимости от времени проекции скорости и координаты тела, брошенного вертикально вверх с начальной скоростью \( v_0 \) (ось Y направлена вертикально вверх): \( v_y=v_<0y>+g_yt;y=y_0+v_<0y>t+g_yt^2/2 \) . Если тело брошено из начала координат, то \( y_0=0 \) и \( y=v_0t-gt^2/2,v_y=v_0-gt \) .
9. График зависимости модуля скорости от времени при движении тела вертикально вверх приведён на рисунке (рис. 27).
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Свободное падение — это
1) любое движение тела в безвоздушном пространстве
2) движение тела вертикально вверх в безвоздушном пространстве
3) падение тела в безвоздушном пространстве
4) падение тела в как безвоздушном пространстве, так и в воздухе
2. В трубке, из которой откачали воздух, одновременно с одной высоты начали падать три шарика: пенопластовый, пластилиновый и железный. Какой из шариков раньше коснется дна трубки?
1) пенопластовый
2) пластилиновый
3) железный
4) все шарики коснутся дна одновременно
3. Значение ускорения свободного падения зависит от
А. Массы тела.
Б. Широты местности.
Верными являются ответы:
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
4. Мяч падает с одинаковой высоты на поверхность Земли из состояния покоя на экваторе и на широте Москвы. В отсутствие сопротивления воздуха время падения мяча на экваторе
1) равно времени его падения на широте Москвы
2) больше времени его падения на широте Москвы
3) меньше времени его падения на широте Москвы
4) ответ может быть любым в зависимости от объёма
5. Мяч падает с одинаковой высоты на поверхность Земли из состояния покоя на экваторе и на широте Москвы. В отсутствие сопротивления воздуха скорость мяча у поверхности Земли на экваторе
1) равна его скорости на широте Москвы
2) больше его скорости на широте Москвы
3) меньше его скорости на широте Москвы
4) ответ может быть любым в зависимости от объёма
6. По какой формуле рассчитывается модуль скорости тела, брошенного вертикально вверх с поверхности Земли
1) \( v=v_0+gt \)
2) \( v=v_0-gt \)
3) \( v=v_0+gt/2 \)
4) \( v=gt \)
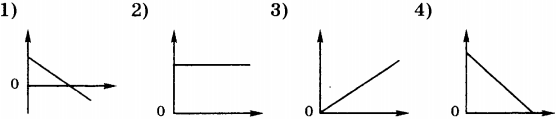
7. Какой из приведённых ниже графиков является графиком зависимости модуля скорости от времени свободного падения тела?
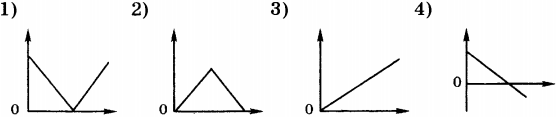
8. Какой из приведённых ниже графиков является графиком зависимости от времени проекции скорости тела, брошенного вертикально вверх, достигшего верхней точки и затем упавшего на Землю?
9. Чему равен модуль скорости свободно падающего тела через 4 с после начала падения?
1) 0,4 м/с
2) 4 м/с
3) 40 м/с
4) 160 м/с
10. На какую высоту поднимется тело, брошенное вверх со скоростью 20 м/с?
1) 20 м
2) 10 м
3) 2 м
4) 1 м
11. Тело, брошенное вертикально вверх, долетело до верхней точки и начало падать вниз. Установите соответствие между величиной, приведенной в левом столбце, и характером её изменения, приведенном в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ВЕЛИЧИНА
A) модуль перемещения
Б) путь
B) координата относительно поверхности Земли
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
1) ускорение движения первого тела больше ускорения движения второго тела
2) ускорение движения первого тела равно ускорению движения второго тела
3) скорость падения на Землю второго тела равна скорости падения на Землю первого тела
4) скорость падения на Землю второго тела больше скорости падения на Землю первого тела
5) тела упадут на Землю одновременно
Часть 2
13. Определите время и координату места встречи двух тел, одно из которых надает на землю с высоты 100 м, а другое тело брошено с поверхности Земли вертикально вверх со скоростью 25 м/с.