Через точку пересечения диагоналей параллелограмма проведена прямая докажите что отрезок заключенный
Решение №2188 Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АВ и CD в точках P и Q соответственно.
Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АВ и CD в точках P и Q соответственно. Докажите, что отрезки BP и DQ равны.
Источник: ОГЭ Ященко 2022 (36 вар)
Рассмотрим ΔBOP и ΔDOQ. В них BО = ОD т.к. диагонали параллелограмма точкой пересечения делятся пополам, ∠BOP = ∠DOQ – как вертикальные, ∠PBO = ∠QDO – как накрест лежащие при параллельных прямых BA||СD и секущей BD.
Значит, ΔBOP = ΔDOQ по стороне и двум прилежащим к ней углам. Отсюда следует равенство соответствующих сторон BP = DQ.
Что и требовалось доказать.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4 / 5. Количество оценок: 3
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Решение №1696 Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая …
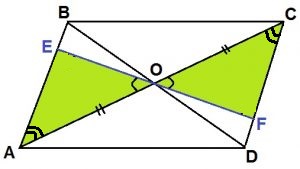
Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АВ и CD в точках E и F соответственно. Докажите, что отрезки АЕ и CF равны.
Источник задания: yagubov.ru
Рассмотрим ΔAEO и ΔCOF. В них AО = ОC т.к. диагонали параллелограмма точкой пересечения делятся пополам, ∠EOA = ∠COF – как вертикальные, ∠EAO = ∠FCO – как накрест лежащие при параллельных прямых BA||СD и секущей АС.
Значит, ΔAEO = ΔCOF по стороне и двум прилежащим к ней углам. Отсюда следует равенство соответствующих сторон AE = CF.
Что и требовалось доказать.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Через точку пересечения диагоналей параллелограмма проведена прямая.
Углы AOB=A’OB’ как вертикальные
Углы OBA=OB’A’ как внутренние накрест лежащие,откуда тк по свойству диагоналей параллелограмма BO=OB’,то треугольники AOB=A’OB’ по стороне и 2 прилежащим углам,откуда AO=OA’
ЧТД.
Через точку О пересечения диагоналей параллелограмма проведем произвольную прямую а, пересекающую параллельные стороны параллелограмма в точках M и N.
Треугольники АМО и CNO равны, так как АО=ОС (диагонали параллелограмма точкой пересечения делятся пополам), угол АОМ равен углу СОN (вертикальные), угол МАО равен углу NСО (внутренние накрест лежащие при параллельных прямых АВ и СD и секущей АС). Из равенства треугольников МО=ОN.
Что и требовалось доказать.
АМ = СК по условию, а СК = ВЕ, значит АМ = ВЕ,
АВ║ЕМ.
Ответ: Две пары параллельных прямых на рисунке.
пирамида КАВС, К-вершина, все ребра=а, проводим амофему КН на АС, КН=АК*корень3/2=а*корень3/2, площадь боковая=1/2 периметрАВС*КН=1/2*3а*а*корень3/2=3*а в квадрате*корень3/4, площадь основания АВС=АС в квадрате*корень3/4=а в квадрате*корень3/4
площадь полная=площадь боковая+площадь основания=3*а в квадрате*корень3/4+а в квадрате*корень3/4=4*а в квадрате*корень3/4=а в квадрате*корень3