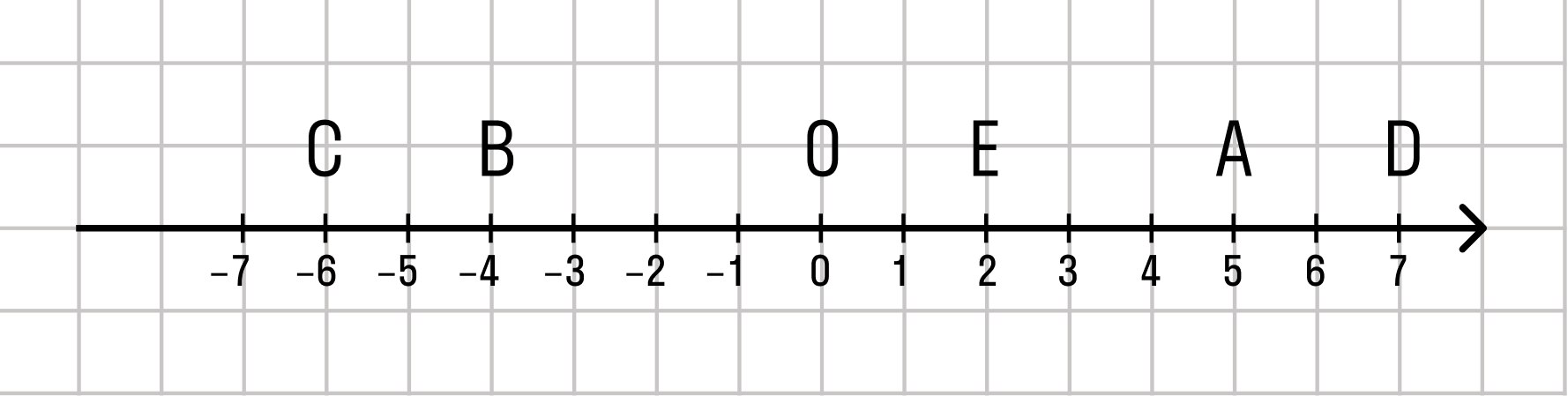
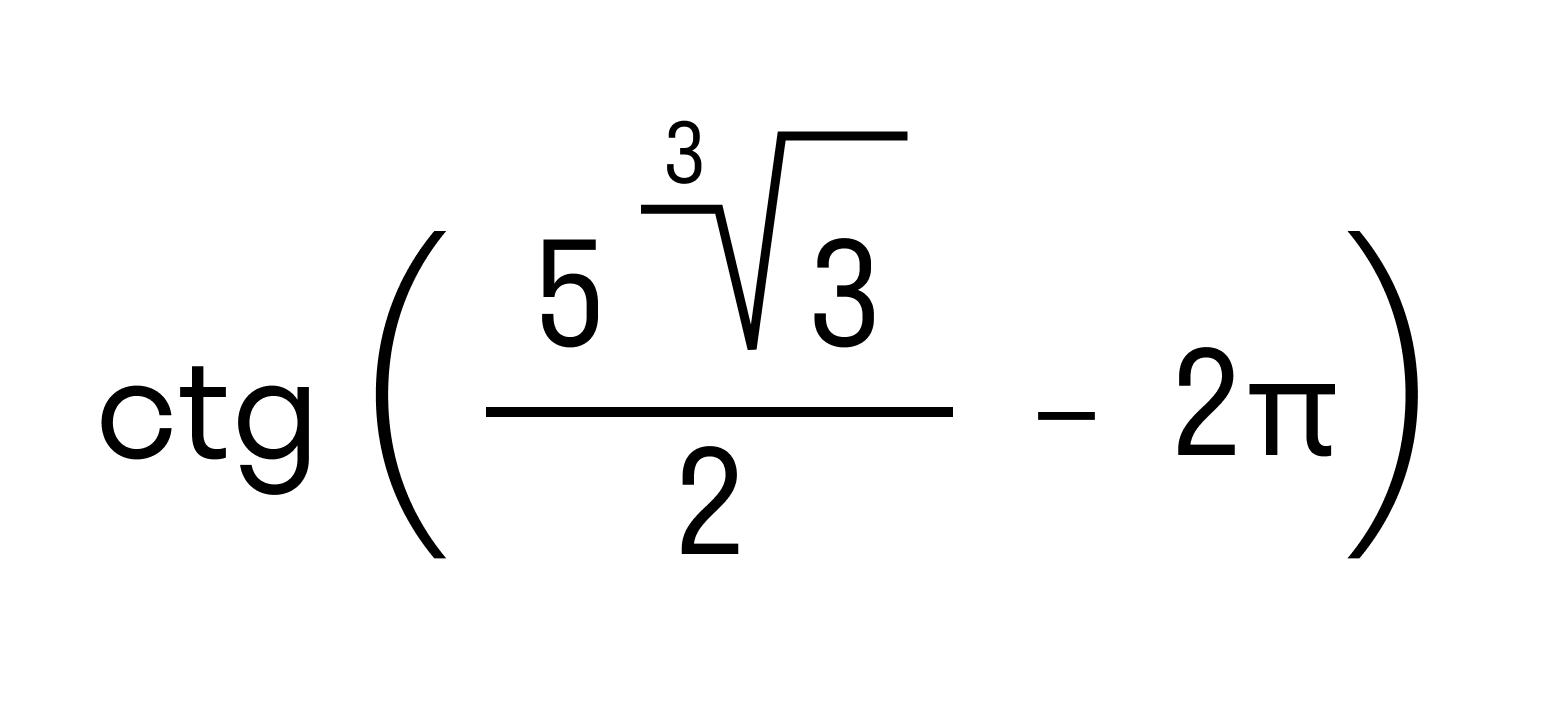Число а такое что а2 4 является действительным

Действительные числа: определение, примеры, представления

Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.

Определение действительных чисел

Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?

Данное определение можно записать иначе с учетом следующего:

Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.

Координатная прямая и действительные числа

Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.

Представления действительных чисел

Под определение дейситвительных чисел попадают:

Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.

Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.

Источник

Тесты по теме: «Комплексные числа»

Просмотр содержимого документа
«Тесты по теме: «Комплексные числа»»

Тест «Комплексные числа»

Часть I. Выберите один правильный ответ.

1. На множестве действительных чисел не выполнима операция:

б) возведения в степень отрицательного числа

в) извлечения арифметического корня из отрицательного числа

2. Комплексные числа были введены для получения дополнительных возможностей при решении:

а) систем линейных уравнений

б) квадратных уравнений

в) уравнений высших степеней

г) тригонометрических уравнений

3. Что представляет собой число i:

а) число, квадратный корень из которого равен – 1

б) число, квадрат которого равен – 1

в) число, квадратный корень из которого равен 1

г) число, квадрат которого равен 1

а) действительных чисел

в) иррациональных чисел

г) комплексных чисел

5. Термин «мнимые числа» ввел:

6. Из предложенных чисел выберите чисто мнимое число:

а) вещественной частью комплексного числа

б) мнимой частью комплексного числа

в) тригонометрической формой комплексного числа

г) алгебраической формой комплексного числа

10. На координатной плоскости число изображается:

а) точкой или радиус-вектором

в) плоской геометрической фигурой

г) заштрихованной частью плоскости

11. Модулем комплексного числа называется:

а) данное комплексное число без учета знака

б) расстояние от начала координат до точки, в виде которой отображается комплексное число

в) расстояние от осей координат до точки, в виде которой отображается комплексное число

г) сумма вещественной и мнимой части

12. Модуль комплексного числа z= 4 + 3i равен:

Источник

Разноуровневые самостоятельные работы «Комплексные числа»

Разделы: Математика

§32 Комплексные числа и арифметические операции над ними.

Тест№1

Цель: проверить знание определения комплексного числа, сопряженных чисел, умения находить действительную и мнимую части комплексного числа.

Прочитайте каждое утверждение, если вы с ним согласны то в колонке ответов поставьте «+», если же вы не согласны с данным утверждением, поставьте « – » в колонке ответов.

Вариант 1

1Число является комплексным.

2Число а, такое что а 2 = – 2 является действительным.

3Число а, такое что а 4 = 1 является действительным.

40 – комплексное число.

5Число 3i является чисто мнимым.

6Действительная и мнимая части комплексного числа 3 – 2i соответственно равны 3 и 2.

7Действительная и мнимая части сопряженных чисел отличаются только знаками.

8Сопряженным для действительного числа является само это число.

9Если, то действительная часть числа z равна 0.

Вариант 2

1Число 5 является комплексным.

2Число а, такое что а 2 = 4 является действительным.

3Число а, такое что а 8 = 1 является действительным.

5Если а + bi является действительным, то b = 0

6Действительная и мнимая части комплексного числа – 3 + 2i соответственно равны – 3 и 2.

7Мнимые части сопряженных чисел отличаются только знаками.

8Если, то мнимая часть числа z равна 0.

Самостоятельная работа №1

Вариант 31Даны числа: .

a)
b)
c)
d)
e)

a)
b)
c)
d)
e)

a)
b)
c)
d)
e)

2Для чисел найдите действительные числа а и b, для которых верно равенство .Для чисел найдите действительные числа а и b, для которых верно равенство .Для чисел найдите действительные числа а и b, для которых верно равенство .3Запишите z в алгебраической форме:

Вариант №3 рассчитан для более подготовленных детей.

§33 Комплексные числа и координатная плоскость.

Самостоятельная работа №2

Цель: проверить умение изображать комплексные числа в комплексной плоскости и производить операции над ними.

§34 Тригонометрическая форма записи комплексного числа.

Цели:

Тест №2

Цель: проверить умение применять геометрическую интерпретацию модуля.

Задание: Сопоставьте друг другу условие на комплексное число z и соответствующее ему множество точек координатной плоскости.

Вариант №1

А1Круг с центром (1; 0) и радиусом 3

Б2Часть плоскости вне круга с центром (0; 0) и радиусом 3

В3Прямая х = 0

Г4Круг с центром (0; 0) и радиусом 3

Д5Круг с центром (0; 1) и радиусом 36Окружность с центром (0; 0) и радиусом 3

Вариант №2

А1Часть плоскости вне круга с центром (0;0) и радиусом 3, включая границу.

Б2Прямая у = – х

В3Окружность с центром (0; – 2) и радиусом 3

Г4Круг с центром (2; – 1) и радиусом 3

Д5Круг с центром (0;2) и радиусом 36Окружность с центром (0; 0) и радиусом 3

Тест №3

Цель: проверить знание определения аргумента и модуля.

Прочитайте каждое утверждение, если вы с ним согласны, то в колонке ответов поставьте «+», если же вы не согласны с данным утверждением, поставьте « – » в колонке ответов.

Вариант 1

1Точки плоскости, удовлетворяющие условию , лежат на окружности радиуса 1.

2Два комплексных числа равны, если равны их аргументы.

3Точки плоскости, у которых аrg z = , лежат на открытом луче выходящим из (0; 0) и имеющим угол, равный 180 о С положительным направлением действительной оси.

4Множество всех комплексных чисел, у которых равны модули, есть окружность.

5При умножении комплексных чисел модули и аргументы перемножаются.

6При делении комплексных чисел модули делятся, а аргументы вычитаются.

7У сопряженных комплексных чисел модули равны.

Вариант 2

1Точки плоскости, удовлетворяющие условию , лежат на окружности радиуса 2.

2Два комплексных числа равны, если равны их модули.

3Точки плоскости, у которых аrg z = –, лежат на открытом луче выходящим из (0;0) и имеющим угол, равный – 90 о С положительным направлением действительной оси.

4Множество всех комплексных чисел, у которых равны аргументы, есть открытый числовой луч, выходящий из начала координат и наклонённый под углом к положительному направлению оси абсцисс.

5При умножении комплексных чисел модули перемножаются, а аргументы складываются.

6При делении комплексных чисел модули и аргументы делятся.

7У сопряженных комплексных чисел аргументы противоположны.

Самостоятельная №3

Цель: проверить умение находить модуль комплексного числа.

Вариант 1

И проверьте следующие неравенства

И проверьте следующие неравенства

Сложность варианта 2 выше, т.к. прежде чем находить модули нужно преобразовать числа в алгебраическую форму.

Самостоятельная работа №4

Цель: проверить умение находить модуль и аргумент комплексного числа, переводить из алгебраической в тригонометрическую форму

Вариант 1

Вариант 2

Вариант 3

Вариант 41. Представьте комплексное число в тригонометрической форме:

а)
b) 1. Представьте комплексное число в тригонометрической форме:

а)
b) 1. Представьте комплексное число в тригонометрической форме:

а)
b) 1. Представьте комплексное число в тригонометрической форме:

а)
b) 2. Даны числа:

§35 Комплексные числа и квадратные уравнения

Цель: научить решать квадратные уравнения с дискриминантом меньшим нуля, извлекать квадратные корни из комплексных чисел в арифметической и тригонометрической форме.

Самостоятельная работа №5

Цель: проверить умение применять определение мнимой единицы при разложении на множители с помощью формул сокращенного умножения, атак же умения решать квадратные уравнения с действительными коэффициентами.

Вариант 1

Вариант 21. Разложите на линейные множители:

a)
b)
c)
d)
e)

a)
b)
c)
d)
e)

a)
b)
с)

a)
b)
c)

Источник

Действительные числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение действительных чисел

Рациональные числа объединяют в себе целые числа и дробные числа. А действительные числа объединяют рациональные и иррациональные числа. Отсюда сформулируем определение действительных чисел:

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Множество рациональных чисел —

Иррациональное число — это число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби m/n. Оно может быть выражено в форме бесконечной непериодической десятичной дроби. Множество иррациональных чисел —

Множество действительных чисел состоит из множества рациональных чисел вместе с множеством иррациональных чисел. Это множество R иначе обозначается как область действительных чисел (-∞; +∞). Можно записать так, что R есть объединение двух множеств: рациональных и иррациональных чисел:

Так как любое рациональное число может быть записано в виде конечной десятичной дроби или бесконечной периодической дроби, а иррациональные числа представляются бесконечными непериодическими десятичными дробями, то определение действительных чисел можно сформулировать по-другому.

Действительные числа — это числа, которые можно записать в виде конечной или бесконечной, периодической или непериодической десятичной дроби. Их иногда называют вещественными.

Примеры действительных чисел:

Число нуль также является действительным числом, так как 0 — рациональное число.

Из определения действительных чисел можно сделать вывод, что существуют как положительные, так и отрицательные действительные числа, а нуль — ни положительное, ни отрицательное действительное число.

При помощи действительных чисел можно описать величины, значения которых могут изменяться непрерывно. Проще говоря, действительные числа дают возможность численно выражать значение непрерывно изменяющейся величины через единичное значение этой величины.

Действительные числа на координатной прямой

Координатная прямая — это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.

Интересный факт: действительные числа заполняют каждую точку координатной прямой.

Каждой точке координатной прямой соответствует единственное действительное число — координата этой точки. При этом каждому действительному числу соответствует единственная точка на координатной прямой. То есть, между действительными числами и точками координатной прямой существует взаимно однозначное соответствие.

Представления действительных чисел

По определению действительными числами являются:

Часто можно встретить действительные числа в виде корней, степеней, логарифмов и др. Кроме того, сумма, разность, произведение и частное действительных чисел также представляют собой действительные числа.

Также из действительных чисел с помощью арифметических знаков, знаков корня, степеней, логарифмических, тригонометрических функций можно составлять числовые выражения, значения которых также будут действительными числами. Например, значения выражений

будут действительные числа.

Сравнение действительных чисел

Любые действительные числа можно сравнивать. Для сравнения действительных чисел есть два способа:

Источник

Модуль числа

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение модуля числа

Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.

Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».

Знак модуля: |a| = OA.

Разберем на примере:

Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.

Число 3 (длину отрезка OB) называют модулем числа −3.

Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).

Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.

Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.

Также можно опустить плюс и записать значение, как |4| = 4.

Записывайся на занятия по математике для учеников с 1 по 11 классы.

Свойства модуля числа

Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.

1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:

2. Модуль положительного числа равен самому числу.

3. Модуль отрицательного числа равен противоположному числу.

4. Модуль нуля равен нулю.

5. Противоположные числа имеют равные модули.

6. Модуль произведения равен произведению модулей этих чисел.

Геометрическая интерпретация модуля

Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.

Нарисуем числовую прямую и отобразим это на ней.

Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.

Решим уравнение: |х| = 5.

Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.

График функции

График функции равен y = |х|.

Для x > 0 имеем y = x.

Этот график можно использовать при решении уравнений и неравенств.

Корень из квадрата

Оно равно a при а > 0 и −а, при а

Модуль комплексного числа

Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:

Свойства модуля комплексных чисел

Модуль рационального числа

Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.

Модуль рационального числа, примеры:

Модуль вещественных чисел

Модуль противоположного числа, нуля, отрицательного и положительного чисел

Закрепим свойства модуля числа, которые мы рассмотрели выше:

Источник