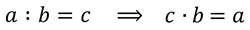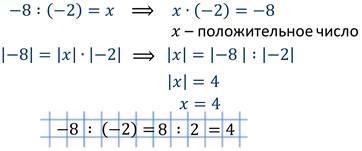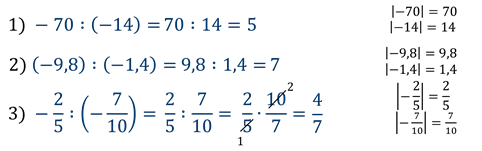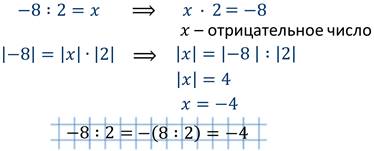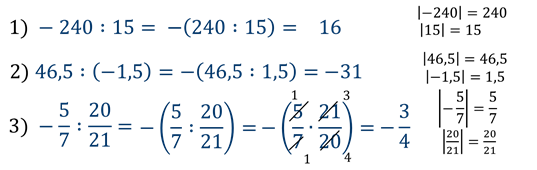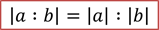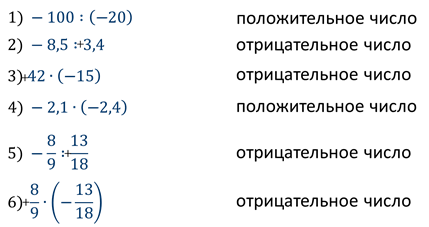Число с минусом разделить на число с минусом что получится
Деление отрицательных чисел
Как выполнять деление отрицательных чисел легко понять, вспомнив, что деление — это действие, обратное умножению.
Если « a » и « b » положительные числа, то разделить число « a » на число « b », значит найти такое число « с », которое при умножении на « b » даёт число « a ».
Данное определение деления действует для любых рациональных чисел, если делители отличны от нуля.
Поэтому, например, разделить число « −15 » на число 5 — значит, найти такое число, которое при умножении на число 5 даёт число « −15 ». Таким числом будет « −3 », так как
Примеры деления рациональных чисел.
Из примеров видно, что частное двух чисел с одинаковыми знаками — число положительное (примеры 1, 2), а частное двух чисел с разными знаками— число отрицательное (примеры 3, 4).
Правила деления отрицательных чисел
Чтобы найти модуль частного, нужно разделить модуль делимого на модуль делителя.
Итак, чтобы разделить два числа с одинаковыми знаками, надо:
Примеры деления чисел с одинаковыми знаками:
Чтобы разделить два числа с разными знаками, надо:
Примеры деления чисел с разными знаками:
Для определения знака частного можно также пользоваться следующей таблицей.
Правило знаков при делении
При вычислении «длинных» выражений, в которых фигурируют только умножение и деление, пользоваться правилом знаков очень удобно. Например, для вычисления дроби
Можно обратить внимание, что в числителе два знака «минус», которые при умножении дадут «плюс». Также в знаменателе три знака «минус», которые при умножении дадут «минус». Поэтому в конце результат получится со знаком «минус».
Сокращение дроби (дальнейшие действия с модулями чисел) выполняется также, как и раньше:
Частное от деления нуля на число, отличное от нуля, равно нулю.
Все известные ранее правила деления на единицу действуют и на множество рациональных чисел.
Зависимости между результатами умножения и деления, известные для положительных чисел, сохраняются и для всех рациональных чисел (кроме числа нуль):
Данные зависимости используются для нахождения неизвестного множителя, делимого и делителя (при решении уравнений), а также для проверки результатов умножения и деления.
Пример нахождения неизвестного.
Знак «минус» в дробях
Разделим число « −5 » на « 6 » и число « 5 » на « −6 ».
Напоминаем, что черта в записи обыкновенной дроби — это тот же знак деления, поэтому можно записать частное каждого из этих действий в виде отрицательной дроби.
Таким образом знак «минус» в дроби может находиться:
При записи отрицательных дробей знак «минус» можно ставить перед дробью, переносить его из числителя в знаменатель или из знаменателя в числитель.
Это часто используется при выполнении действий с дробями, облегчая вычисления.
Пример. Обратите внимание, что после вынесения знака «минуса» перед скобкой мы из большего модуля вычитаем меньший по правилам сложения чисел с разными знаками.
Используя описанное свойство переноса знака в дроби, можно действовать, не выясняя, модуль какого из данных дробных чисел больше.
Как разделить отрицательные числа?
Деление отрицательных. Как делить два отрицательных числа. Как разделить, если одно число отрицательное. И разделим отрицательные числа на калькуляторе!
Для деления отрицательных чисел существует только два пункта правил!
О делении отрицательных.
Правило деления отрицательных чисел.
Правила деления отрицательных аналогично умножению, только отличие в знаке.
1). Когда делимое и делить отрицательные
Первый пункт правил деления отрицательных чисел звучит так : «если делимое a и делитель b » отрицательные, то минус на минус дает плюс, т.е. результат(частное с) будет положительным:
2). Когда при делении только одно число отрицательное
Как разделить отрицательные числа.
Заменяем наши буквы на числа и получим пример деления отрицательных чисел.
(-15) : (-12) = 15 : 12 = 1.25
Как разделить отрицательные числа на калькуляторе.
Как и в предыдущем пункте заменяем буквенные значения на числовые.
Как разделить отрицательные числа на калькуляторе.
Следующим пунктом, мы разделим два отрицательных числа на калькуляторе
Набираем делимое 12.
Набираем делитель : 15.
Меняем знак на отрицательный, кнопкой плюс/минус : «±».
Получаем результат деления двух отрицательных чисел.
Как разделить отрицательное на положительное на калькуляторе.
Делим отрицательные на калькуляторе, когда только одно число отрицательное:
Набираем делимое 12.
Набираем делитель : 15.
Получаем результат деления двух отрицательных чисел, когда лишь одно число отрицательное.
Деление
Урок 37. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Деление»
Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел. Напомним, что деление – это действие, обратное умножению.
Как известно, разделить число на а на число b – это значит найти такое число с, которое при умножении на b даёт а.
Разделим число –8 на число –2. Т.е. надо найти такое число х, которое при умножении на –2 даст число –8.
Чтобы разделить отрицательное число на отрицательное, нужно модуль делимого разделить на модуль делителя.
Запомните! Частное двух отрицательных чисел – это положительное число.
Делить отрицательные числа мы научились. Рассуждая аналогичным образом, давайте разберёмся, как делят числа с разными знаками.
Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «минус».
Обратите внимание, что не имеет значение перед делимым или делителем стоит знак «минус». Частное двух чисел с разными знаками – это отрицательное число.
Вам хорошо известны свойства числа 1, записанные следующими формулами:
Эти свойства сохраняются и когда а – отрицательное число. Убедимся в этом.
Если делимое равно 0, а делитель – любое число, отличное от 0, то частное равно 0.
Не забывайте, что на 0 делить нельзя!
Модуль частного двух чисел равен частному их модулей.
А знак частного зависит от знаков делимого и делителя: если делимое и делитель имеют одинаковые знаки (т.е. оба положительны или оба отрицательны), то частное положительно, а если разные – отрицательно.
Рассмотрим таблицу, которая наглядно показывает зависимость знака частного от знаков делимого и делителя:
Запомнить эту таблицу очень легко. Смотрите, при делении чисел с одинаковыми знаками получается положительное число, а при делении чисел с разными знаками – отрицательное.
Упражнение: определите знак произведения и частного.
Чтобы разделить отрицательное число на отрицательное, нужно модуль делимого разделить на модуль делителя.
Частное двух отрицательных чисел – это положительное число.
Чтобы разделить числа с разными знаками, нужно модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «минус».
Частное двух чисел с разными знаками – это отрицательное число.
Урок 37 Бесплатно Деление
В прошлом уроке мы познакомились с умножением.
Сейчас перейдем к делению, узнаем правила деления для чисел с разными знаками, деления отрицательных чисел, проведем параллели между умножением и делением, а также определим, какой может быть знак результата деления в зависимости от знаков делимого и делителя.
Деление отрицательных чисел
Правило: для того, чтобы разделить одно отрицательное число на другое отрицательное число, необходимо разделить модуль первого числа на модуль второго числа.
Это правило очень похоже на правило для умножения. Откуда такая схожесть мы узнаем чуть позже, а пока посмотрим на примеры.
Пример:
Допустим надо разделить -15 на -5
1) Найдем модули от этих чисел:
2) Посчитаем частное этих двух чисел:
Пример:
Разделим -132 на -3
1) Находим модули этих чисел:
2) Посчитаем частное модулей:
Это правило работает для нецелых чисел:
2) Выполняем деление:
И еще несколько примеров уже менее подробно:
Пройти тест и получить оценку можно после входа или регистрации
Деление чисел с разными знаками
Допустим, мы знаем, что на заводе 250 работников, получающих одинаковую зарплату, также мы знаем, что вся сумма денег на выплату зарплат изменилась на -100000 рублей.
На сколько изменилась зарплата каждого конкретного работника?
Необходимо разделить общее изменение на количество работников. Иными словами, необходимо разделить отрицательное число на положительное.
Правило: чтобы разделить отрицательное число на число положительное, нужно поделить модуль первого числа на модуль второго числа и к результату деления приписать минус.
Воспользуемся им для решения задачи:
1) Берем модули чисел:
3) И приписываем к результату минус:
Получаем, что зарплата каждого работника изменилась на -400 рублей, иными словами, уменьшилась на 400 рублей.
Теперь посмотрим, как разделить положительное число на отрицательное.
Правило: чтобы разделить положительное число на число отрицательное, нужно поделить модуль первого числа на модуль второго числа и к результату приписать минус.
Допустим, необходимо разделить 161 на -7:
1) Посчитаем модули:
2) Посчитаем частное:
3) И приписываем к нему минус:
Это и будет ответом.
Заметим, что оба правила достаточно похожи, поэтому можно их обобщить и запомнить общее правило.
Правило: чтобы посчитать частное чисел с разными знаками, необходимо посчитать частное их модулей и приписать к нему минус.
Пройти тест и получить оценку можно после входа или регистрации
Сведение деления к умножению
Вы уже могли заметить, что правила для умножения и деления весьма похожи. Это вполне закономерно.
Как мы уже говорили в уроке про деление дробей, деление можно заменить умножением делимого на число, обратное делителю.
И это верно для отрицательных чисел тоже.
Посмотрим, как это происходит на примерах.
1-й способ: воспользоваться правилом для деления отрицательных чисел:
2-й способ: представить деление как умножение на число, обратное делителю, и воспользоваться правилом для умножения отрицательных чисел:
Как вы можете заметить, результаты вычислений разными подходами совпадают. Более того, совпадают даже последние действия, поэтому можете выбирать любой удобный для вас способ.
Такой же подход работает и для деления чисел с разными знаками.
Пример:
1-й способ: воспользуемся правилом для деления чисел с разными знаками:
2-й способ: заменим деление на умножение и воспользуемся правилом для умножения чисел с разными знаками:
Можно заметить, что результаты совпадают.
Так что можно выбирать любой способ для выполнения деления чисел с разными знаками.
Пройти тест и получить оценку можно после входа или регистрации
Определение знака частного
Если мы хотим определить, какой знак будет у частного, не считая его, тогда нам помогут следующие правила:
Правило: частное двух отрицательных чисел всегда число положительное
Пример:
Частное \(\mathbf<-32>\) и \(\mathbf<-4>\) будет больше нуля.
Правило: частное положительного числа и отрицательного равно нулю
Пример 1:
Частное 45 и \(\mathbf<-5>\) будет меньше нуля.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Мы уже говорили о площади круга и площади квадрата.
Эти знания нам сейчас пригодятся, потому что так мы можем найти математическую ошибку в одном литературном произведении, а именно, в романе Джека Лондона «Маленькая хозяйка большого дома».
«Посреди поля возвышался стальной шест, врытый глубоко в землю. С верхушки шеста к краю поля тянулся трос, прикреплённый к трактору. Механики нажали рычаг, и мотор заработал.
Машина сама двинулась вперёд, описывая окружность вокруг шеста, служившего его центром.
– Чтобы окончательно усовершенствовать машину, Грэхем, вам остаётся превратить окружность, которую она описывает, в квадрат.
– Да, на квадратном поле пропадает при такой системе очень много земли.
Грэхем произвёл некоторые вычисления, затем заметил:
– Теряем примерно три акра из каждых десяти.
И сейчас мы проверим, прав ли был Грэхем.
Посчитаем площадь квадрата: возводим длину сторон х в квадрат.
Так что площадь квадрата- \(\mathbf
Теперь посчитаем площадь круга: \(\mathbf<\pi(\frac
Теперь мы можем вычесть из площади квадрата площадь круга и понять, какая часть площади не используется.
Как мы видим, не используется 0.22 земли, что явно меньше 0.3, о которых говорится в тексте.
Возможно, так автор хотел изобразить математическое невежество героев, или же он просто не уделил внимание таким подробностям.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Деление отрицательных чисел: правило и примеры
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Правило деления отрицательных чисел
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.
Перейдем к рассмотрению примеров.
Деление отрицательных чисел. Примеры
Начнем с простых случаяв, переходя к более сложным.
Пример 1. Как делить отрицательные числа
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Пример 3. Как делить отрицательные числа
Теперь можно выбрать один из двух способов:
Разберем оба способа.
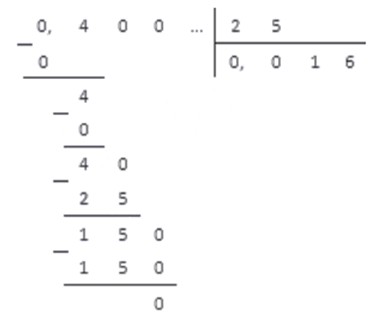
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Пример 4. Как делить отрицательные числа