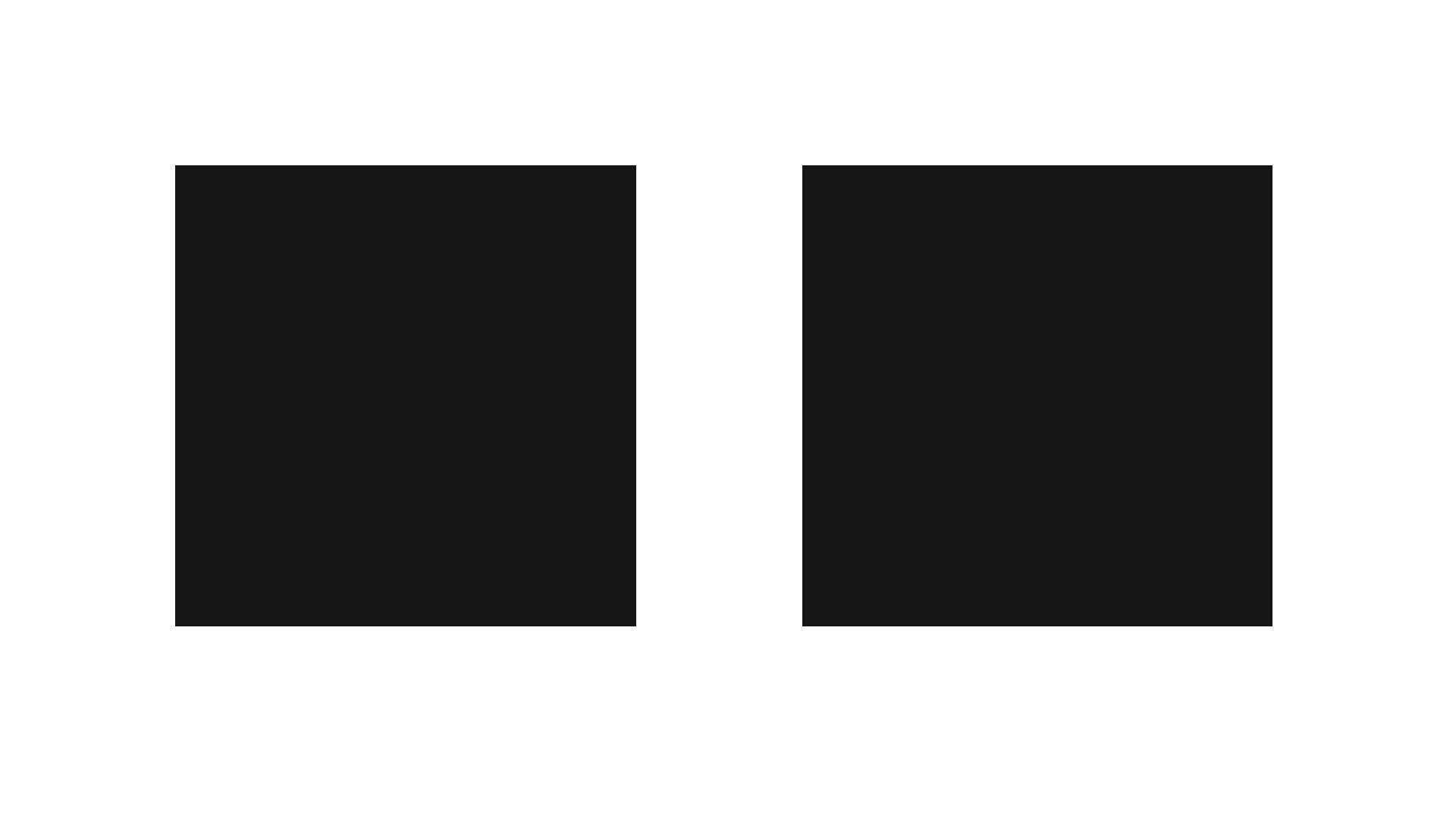Что больше круг или квадрат одинакового размера
Как работает оптический баланс в дизайне
Кому-то лаконичный дизайн покажется набором кругов, треугольников и квадратов, которые расставит в ряд даже ребёнок. Но всё не так просто.
Наше визуальное восприятие несовершенно: безошибочно вычислить ровный круг среди овалов или квадрат среди прямоугольников сможет только человек с намётанным глазом. Большинству людей искажённые пропорции покажутся идеальными:
Неверное восприятие формы квадрата связано с тем, что мы подсознательно удлиняем вертикальные линии и укорачиваем горизонтальные. И это не единственная ошибка восприятия. Обман зрения подстерегает нас на каждом шагу.
Поэтому геометрическая точность — лишь один из факторов, который учитывают в дизайне. Важнее добиться оптического баланса — чтобы элементы казались зрителю ровными и пропорциональными, даже если это на самом деле не так. Давайте посмотрим, как особенности нашего восприятия сказываются на дизайне.
Пишет о дизайне в Skillbox, а в перерывах и сама орудует графическим планшетом. Влюблена в советские шрифты, японскую рекламу и русский язык.
Визуальный вес объектов
Визуальный вес — это способность объекта притягивать к себе внимание зрителя. На это влияет много разных вещей. Например, мы неизбежно задерживаем взгляд на детализированных изображениях. А также на тех, которые расположены по центру или обособленно от других — в обширном белом пространстве.
Но если по технике исполнения и композиционному расположению объекты равны, это вовсе не значит, что они будут равнозначны для зрителя. Потому что есть ещё два фактора, влияющие на визуальный вес, — это размер и цвет. И с ними тоже не всё так просто, как кажется.
Размер и визуальный вес объектов
Казалось бы, при прочих равных условиях одинаковым визуальным весом должны обладать объекты, у которых одинаковая ширина и высота. Но это не так. Взгляните на квадрат и круг одинакового размера:
Несмотря на равные ширину и высоту, квадрат кажется ощутимо крупнее круга. И дело не только в том, что общая площадь больше. Важно, что у него больше площадь соприкосновения с горизонтальными и вертикальными осями, с помощью которых сравнивают фигуры. Даже если мы не чертим эти линии, то проводим их мысленно — когда соотносим один объект с другим. И круг, скажем, касается верхней границы всего в одной точке, в то время как квадрат охватывает свою верхнюю границу целиком.
Чтобы фигуры казались нам равными, круг должен быть немного крупнее квадрата:
Теперь объекты на вид равны по размеру — хотя в действительности круг больше. Этот эффект называется « оптический размер».
Хотите усвоить правила композиции, разобраться в элементах веб-интерфейсов и научиться создавать красивые сайты? Записывайтесь на наш курс по веб-дизайну!
Несоответствие между геометрическими и оптическими размерами фигур становится проблемой для дизайнера, когда нужно создать равные по визуальному весу элементы — например, иконки на сайте. Обычно иконки имеют разную форму: одни тяготеют к квадрату, другие будут круглыми или вытянутыми, одни представляют собой однотонное пятно цвета, а в других не обойтись без мелких деталей. Всё зависит от того, какие именно понятия нужно показать в изображениях.
Если форма иконок сильно разнится, делать их одинаковыми по ширине и высоте — плохое решение. Чтобы они казались зрителю одинаковыми, подбирают размер каждой картинки исходя из её очертаний. Посмотрите на этот пример:
Что больше площадь круга или квадрата
0,7-0,8 мкв (лень высчитывать на калькуляторе)
Длина окружности 4м, площадь
1.2-1.3мкв.
Вывод – чем в фигуре углы острее – тем меньше ее площадь (при одинаковом периметре). Круг не имеет углов = максимально возможная площадь при заданном периметре.
Наглядно – берем квадрат, и начинаем сжимать его за вершины, чтоб он трансформировался в ромб. И перед тем как он превратиться в прямую – его площадь будет стремиться к нулю. При этом периметр неизменен.
Почему на практике у нас дома не круглые? потому как заполнить всю площадь (объем) круга (сферы) можно лишь сравнительно мелкими материальными объектами. Жидкости, газы, песок.. (наверно по этому цистерны все круглые). А при попытке забить круглую комнату угловатыми коробками – полезный объем уменьшается. Ну как то так
Круг – это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом. В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром. Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно: Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Существует формула площади круга через диаметр. Она также широко применяется для вычисления необходимых параметров. Данные формулы можно использовать для нахождения площади треугольника по площади описанной окружности.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности: 
Теперь подставим это равенство в формулу расчета площади круга и получим формулу нахождения площади круга, через длину окружности
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: 
отсюда 
.
После того, как найдем диагональ – мы сможем рассчитать радиус: 
.
И после подставим все в основную формулу площади круга описанного вокруг квадрата: 
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.
Окружность и круг — в чём отличие?
Окружность — замкнутая плоская кривая, все точки которой равноудалены от одной заданной точки — центра окружности.
Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.
Квадратура круга: наглядное доказательство
Словесные доказательства с трудом даются тем, кто привык мыслить визуально. Поэтому в математике так важна визуальная интуиция. Доказательства из таких пособий, как и «Евклид Начала: первые 6 книг» и «Доказательства без слов: учебник по визуальному мышлению» даются пониманию при взгляде на их страницы. Я рекомендую эти книги к прочтению каждому, кто интересуется доказательствами других математических проблем.
К примеру, мы помним из школьного курса, что площадь круга вычисляется по формуле π x r², но можем ли мы доказать, что эта формула справедлива для каждой возможной окружности?
Величайший из математиков Евклид нашёл доказательства этой формулы настолько простое, что теперь студенты изучают начала интегрального исчисления по нему. Евклид рассуждал так: круг можно поделить на четыре, шесть, шестнадцать, или бесконечно много равных частей, а потом расставить их так, чтобы получился прямоугольник.
Первое что нам нужно сделать — начертить окружность. Затем, мы разделим круг на 8 равных частей и расставим их в похожую на прямоугольник форму. Мы почти получили прямоугольник.
Повторим процесс, на этот раз с 32 равными частями. Если расставить их таким же образом как в предыдущем примере, то мы получим что-то ещё более похожее на прямоугольник.
Это значит, что если разделить круг на ещё больше равных частей — происходит удивительное, форма начинает приближаться к идеальному прямоугольнику.
Насколько много должно быть частей чтобы получить идеальный прямоугольник? Для этого его части должны быть бесконечно малыми — такими, что невозможно различить толщину, и стороны становятся почти вертикальными.
Таким образом, πr² может использоваться для вычисления площади любой из существующих окружностей.
Конспект занятия по ФЭМП «Один и много. Круг и квадрат» (младшая группа)
Надежда Григорьева
Конспект занятия по ФЭМП «Один и много. Круг и квадрат» (младшая группа)
-Продолжать совершенствовать умения находить один и много предметов в окружающей обстановке.
-Закреплять умения различать и называть круг и квадрат
-Совершенствовать умение сравнивать два предмета по длине способами наложения и приложения, обозначать результаты сравнения славами (длинны-короткий, длиннее-короче.)
Дидактический наглядный материал:
Раздаточный материал: Карандаши разных цветов (длина 10см и 20см,круг (диаметр 7-8см,квадрат (длина стороны 7-8см).
Ход занятия:
Воспитатель: Со словами «серенькая кошечка села на окошечко» воспитатель сажает ее на подоконник. Ребята давайте мы с вами посмотрим в окно, Что вы видите на улице? Каких предметов много на улице? Каких предметов по одному?
Дети: Деревья,дома,магазин. Много деревьев, домов. Мало магазинов.
Дети: зеленый карандаш длиннее, а желтый короче.
Воспитатель: А теперь поставьте длинный зеленый карандаш в большой стаканчик, а в маленький стакан- короткий карандаш. Маша, в большой стаканчик какой карандаш поставила?
Дети (маша): длинный карандаш
Воспитатель: а в маленький стаканчик какой карандаш поставила?
Дети (Маша): короткий карандаш
Воспитатель: (2-3 индивидуальных вопросов)Молодцы ребята
Подвижная игра: «Найди свой домик»
Воспитатель: давайте мы с вами поиграем, с одной стороны коврика будет лежать квадрат, а с другой круг, это будут домики, сейчас вы возьмете по одной геометрической фигуре с подноса, назовите какие геометрические фигуры у вас в руках?
Дети: круг,квадрат.
Воспитатель: а как вы поняли что это круг или квадрат?
Дети: у квадрата есть углы, а у круга нет углов.
Воспитатель: правильно молодцы, те дети которые взяли квадрат идут в домик квадрата, а у кого круг,к кругу. пока будет играть мелодия вы будете гулять,как только я ее выключу вы находите свой домик. (игра повторяется еще 1 раз, воспитатель меняет местами домики) Молодцы ребята у вас очень хорошо получилось. Садитесь все на свои места. Ребята что мы с вами сегодня делали?
Дети: сравнивали карандаши,искали домики.
Воспитатель: Молодцы, а вам понравилось занятие,мне и кошке очень понравилось.
Воспитатель: вы все были сегодня молодцы,хорошо справлялись с заданием.
Конспект занятия (ФЭМП) «Один-много» МБОУ «Лицей «МОК№2» г. Воронеж 2016г. Цель: закрепить понятия : «один-много, ни одного», узнавание и называние геометрических.
Конспект «Закрепление предметов один-много» (вторая младшая группа) Цель:Обогащение навыков и умений детей на группы предметов:один-много. Задачи. Образовательные: Формировать и закреплять группу предметов.
Конспект НОД по ФЭМП «На помощь к трем поросятам. Большой, маленький. Один, много, ни одного. Круг и квадрат» Конспект занятия НОД на тему «На помощь к трем поросятам» ОО «Познавательное развитие» Формирование элементарных математических представлений.
Конспект занятия по ФЭМП во второй младшей группе «Один. Много» Тема: Один. Много. Цель: Учить находить в окружающей обстановке много однородных предметов и выделять из нее один предмет. Задачи: Познакомить.
Конспект занятия по ФЭМП во второй младшей группе «Много, мало, один» Вторая младшая группа Воспитатель:Матрохина Г. А. Тема: Много, мало, один Цель занятия: упражняться в составлении групп отдельных предметов,учить.
Конспект занятия по ФЭМП в первой младшей группе «Один, много» Конспект занятия по ФЭМП в 1 младшей группе «Один, много» Цель: формирование элементарных математических представление: один, много. Задачи:.
Конспект занятия по познавательному развитию (ФЭМП) во второй младшей группе «Геометрические фигуры: квадрат, круг» Конспект занятия по познавательному развитию (ФЭМП) во второй младшей группе «Геометрические фигуры: квадрат, круг» Цель: Познакомить детей.
Конспект занятия по ФЭМП «Гирлянды к празднику» для второй младшей группы
Татьяна Рымшина
Конспект занятия по ФЭМП «Гирлянды к празднику» для второй младшей группы
Гирлянды к празднику
1. Формировать представление о форме предметов и сравнении предметов по форме (одинаковая, разная, умение группировать предметы по форме;
2. Закреплять умение определять и называть цвет и размер предметов;
3. Формировать в простейших случаях умение видеть закономерность и составлять ряд закономерно чередующихся фигур.
Демонстрационный: белые круг, треугольник, прямоугольник, квадрат. Круги, квадраты и треугольники одного размера разного цвета.
Раздаточный: красные и зеленые треугольники одного размера, красные круги разного размера, по 2 одинаковых листа с нарисованной ниткой на каждого ребенка.
Ход образовательной деятельности
-Что-то в группе приключилось,
Что-то в группе изменилось,
Что не так сегодня, дети?
Посмотрите, кто заметит?
Дети слушают, осматриваются в групповой комнате и замечают «волшебную шкатулочку»
Воспитатель: Посмотрим, что в шкатулке?
Воспитатель открывает шкатулку.
— Здесь, ребята, разные фигуры. Хотите угадать, какие?
Три вершины, три угла,
Три сторонки у меня. Кто же я?
Из этих треугольников можно сделать украшение для нашей группы к празднику.
— Какой праздник скоро будем отмечать? (Новый год)
— Как готовятся к Новому году? (Готовят подарки, наряжают елку)
— Хотите сделать гирлянды из флажков? (показываю на фигуры)
Выкладываю на стол красные и зеленые треугольники одного размера
— Чем флажки отличаются? (Есть красные, а есть зеленые)
— Молодцы! Флажки отличаются по цвету.
Раздаю листы бумаги с нарисованной ниточкой. Слева на нитке нарисован узелок.
— Давайте выберем красный флажок и повесим его на нитку рядом с узелком.
— Рядом повесим зеленый флажок.
— Потом снова красный.
Дети самостоятельно развешивают флажки, воспитатель проверяет.
Задание проверяется у каждого ребенка. Дети любуются гирляндами.
Мы на елке веселились, (ритмичные хлопки в ладоши)
И плясали, и резвились, (ритмичные удары кулачками)
После добрый Дед Мороз («шагают» по столу средним и указательным)
Нам подарки преподнес. (пальцами обеих рук)
Дал большущие пакеты, («рисуют» руками большой круг)
В них же —вкусные предметы: (ритмичные хлопки в ладоши)
Конфеты в бумажках синих, (загибают пальчики на руках)
Орешки рядом с ними,
Приглашаю детей к «волшебной шкатулке».
— Отгадайте,что еще лежит в нашей шкатулке:
Нет углов у меня и похож на блюдце я.
На тарелку и на крышку,
На кольцо и колесо.
Угадайте, друзья, кто же я?
Воспитатель: Верно, молодцы.
Подходим к соседнему столу, выкладываю на стол круги красного цвета, предлагая сделать еще одну красивую гирлянду.
— Одинаковые или разные круги лежат на столе? (Разные)
— Чем круги отличаются? (Есть большие и маленькие)
— Молодцы, круги отличаются по размеру.
— Выберем маленький круг и положим его на нитку рядом с узелком.
— Найдем большой круг и положим его рядом с маленьким.
— Затем какой? (Большой)
Дети развешивают круги самостоятельно, задание у каждого проверяет воспитатель.
Воспитатель собирает детей возле себя и рассказывает, что часть фигур для гирлянд перепуталась. Для того, чтобы можно было ими воспользоваться, их нужно разложить по коробкам.
— Хотите разложить фигуры по коробкам?
Дети вместе с воспитателем подходят к столу, на котором находятся круги, квадраты, треугольники, прямоугольники одного размера, но разного цвета.
Воспитатель показывает детям большой белый круг и говорит, что это как будто коробка.
— В эту коробку нужно положить все фигуры такой же формы.
То же самое происходит с белым квадратом, треугольником и прямоугольником.
— Молодцы! Теперь, когда все разложено по местам, будет очень удобно пользоваться этими фигурами!
— Что мы сегодня делали? (ответы)
— Молодцы! Вы смогли сделать красивые гирлянды на праздник, разложить фигуры по коробкам, потому что знаете цвета и умеете определять форму и размер.
1. Петерсон Л. Г., Кочемасова Е. Е. Игралочка. Практический курс математики для детей 3-4 лет
Конспект НОД по ФЭМП во второй младшей группе «Гирлянды для елочки» НОД по ФЭМП во второй младшей группе. Цель:1. Формировать представление о форме предметов и сравнении предметов по форме (одинаковая, разная,.
Конспект занятия по ФЭМП во второй младшей группе КОНСПЕКТ по ФЭМП во второй младшей группе МБДОУ № 201 г. Кемерово, воспитатель Долгова Татьяна Парфирьевна Программное содержание: 1. Продолжать.
Конспект занятия во второй младшей группе по ФЭМП «Мой дом» Тема: Мой дом. Цель: Способствовать формированию целостной картины мира, расширять кругозор; формировать стремление к познанию окружающего.