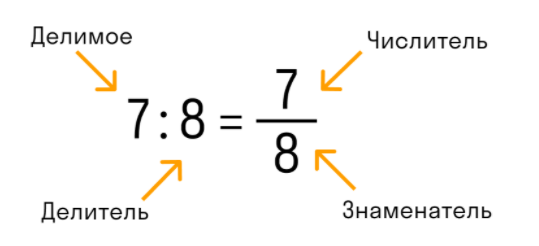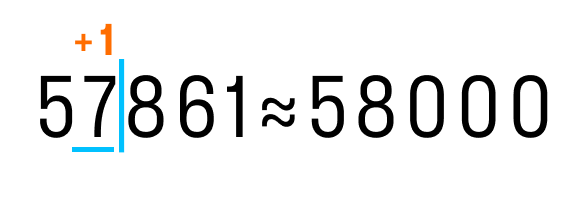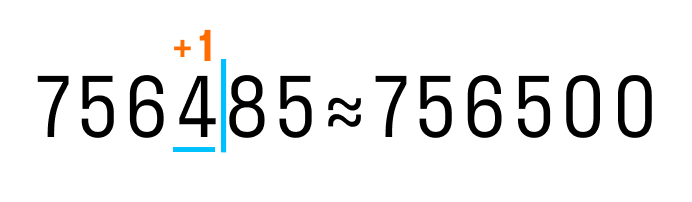Что больше сотые или десятые в десятичной дроби
Сравнение десятичных дробей
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.
Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это когда количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Основные свойства
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Правило сравнения десятичных дробей
Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.
Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.
Алгоритм сравнения десятичных дробей
Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.
Целую часть с целой частью: 15 = 15. Целые части равны.
Десятые с десятыми: 7 = 7. Десятые также равны.
Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.
Сравним 3,656 и 3,48.
Сравнение десятичных дробей
Одно и то же натуральное число может быть представлено в виде обыкновенной дроби разными способами, например, 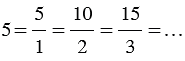
Если к десятичной дроби приписать справа какое угодно количество нулей, то получится дробь равная данной.
Пример:
Пример:
1) 3,40 = 3,4; 2) 0,50600 = 0,506; 3) 5,870000 = 5,87.
| Любое натуральное число можно представить в виде десятичной дроби с каким угодно количеством нулей после запятой. |
Пример:
| Из двух десятичных дробей с разными целыми частями больше та дробь, у которой целая часть больше. |
Пример:
1) 3,5 
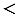
| Из двух десятичных дробей с одинаковыми целыми частями и равным количеством цифр после запятой больше будет та дробь, у которой больше первая (при чтении слева направо) из неодинаковых цифр их дробных частей (поразрядное сравнение). |
Пример:
1) 15,2 
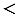

| Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно (смотри правило выше). |
Пример:
Сравнить десятичные дроби 45,6 и 45,498.
Решение:
У дроби 45,6 одна цифра после запятой, а у дроби 45,498 три цифры после запятой, для того, чтобы сравнить данные дроби, приписываем к дроби 45,6 справа два нуля, получим новую дробь 45,600. Теперь поразрядно сравниваем дроби 45,600 и 45,498, получим 45,600 


Поделись с друзьями в социальных сетях:
Урок 41 Бесплатно Сравнение десятичных дробей
Сравнение чисел- это математическая операция, с помощью которой можно установить равенство или неравенство чисел, если числа не равны, то с помощью данной операции можно выяснить какое число больше, а какое меньше.
Сравнивать можно любые числа в том числе и десятичные дроби.
Десятичные дроби будем сравнивать с помощью их десятичной записи.
Сегодня на уроке научимся определять разрядность десятичной дроби, разберем правила сравнения десятичных дробей.
Определим, где на координатном луче расположена десятичная дробь.
Разряды десятичных дробей
В десятичных дробях, так же, как и в натуральных числах, значение каждой цифры зависит от ее места (позиции) в числе.
Каждый знак в записи десятичной дроби означает сколько единиц соответствующего разряда содержится в ней, а единица каждого разряда содержит 10 единиц предыдущего разряда.
В десятичной дроби до запятой (в целой части десятичной дроби) название разрядов точно такое же, как в натуральных числах: единицы, десятки, сотни, тысячи и т.д.
Каждая цифра десятичной дроби, стоящая после десятичной запятой (в дробной части) тоже имеют свое название и значение.
Номер разряда в целой части отсчитывается влево от запятой, а в дробной части- вправо от запятой.
Разряды в десятичных дробях отличаются по старшинству: старшинство убывает слева на право.
Самым старшим (высшим) разрядом считается самая левая цифра в числе, самым младшим разрядом (низшим) разрядом является самая правая цифра в числе.
Цифры, стоящие после десятичной запятой, называют десятичными знаками.
Итак, если после десятичной запятой стоит один знак- это десятые, если после запятой два знака- это сотые, если три десятичных знака- это тысячные и т.д.
Таким образом, первая цифра после запятой обозначает разряд десятых (\(\mathbf<\frac<1> <10>= 0,1>\)), далее идет разряд сотых (\(\mathbf<\frac<1> <100>= 0,01>\)), затем разряд тысячных (\(\mathbf<\frac<1> <1000>= 0,001>\)) и т.д.
Давайте составим таблицу разрядов десятичных дробей.
На основе вышеизложенной информации рассмотрим поясняющий пример.
Составим таблицу разрядов для числа 175,248.
Из таблицы видно, что заданное число 175,248 содержит 1 сотню, 7 десятков, 5 единиц, 2 десятых, 4 сотых, 8 тысячных.
Данная десятичная дробь читается так: «сто семьдесят пять целых двести сорок восемь тысячных».
Наверное, вы заметили, что в нашем примере, в таблице, в разряде десятитысячных мы поставили нуль, и в наших действиях нет никакой ошибки.
Справа от запятой после самой последней цифры, неравной нулю, можно приписывать сколько угодно нулей, от этого значение десятичной дроби не изменится.
75,248 = 75,2480 = 75,24800 = …
Верно и обратное действие: если в конце десятичной дроби, после самой правой ненулевой цифры стоят только нули, то эти нули можно отбросить, в результате получится по значению та же самая дробь.
75,24800 = 75,2480 = 75,248
Нули, стоящие в целой части десятичной дроби, перед самой левой ненулевой цифрой, эту десятичную дробь не изменяют.
75,248 = 075,248 = 0075,248 = 00075,248 = …
У меня есть дополнительная информация к этой части урока!
Нули, стоящие между десятичными знаками, убирать и дописывать ни в коем случае нельзя.
Нуль, стоящий между десятичными знаками несет в себе информацию о том, что в данном разряде отсутствуют единицы.
Например, 2,05 ≠ 2,5.
2,05 и 2,5- это абсолютно два разных числа.
2,05— две целых пять сотых.
2,5— две целых пять десятых.
Любую десятичную дробь можно представить в виде суммы, т.е. разложить по разрядам.
Сумма разрядных слагаемых- это запись числа в виде суммы его разрядных единиц.
Делается это так же просто, как и для натуральных чисел.
Попробуем разложить десятичную дробь по разрядам на примере.
Разложите десятичную дробь 43,2086.
Число 43,2086 содержит следующие разряды:
Число содержит 4 десятка, 3 единицы, 2 десятых, 0 сотых, 8 тысячных, 6 десятитысячных.
В результате получаем:
43,2086 = 40 + 3 + 0,2 + 0,00 + 0,008 + 0,0006
Пройти тест и получить оценку можно после входа или регистрации
Изображение десятичной дроби на координатном луче
Десятичную дробь, как и любое другое число, можно отметить на координатном луче.
Десятичные дроби на координатном луче изображают так же, как обыкновенные дроби (смешанные числа), поскольку десятичная дробь и соответствующая ей обыкновенная дробь- это одно и тоже число.
Для того чтобы отметить на координатном луче точку, которая будет соответствовать заданной десятичной дроби, нужно перевести эту десятичную дробь в обыкновенную дробь (смешанное число).
Отметим на координатном луче точку А(0,5) и точку В(1,3).
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
По условию нам даны десятичные дроби с одним десятичным разрядом, следовательно, соответствующие им обыкновенные дроби, содержат в знаменателе число 10.
Десятичной дроби 0,5 соответствует обыкновенная правильная дробь \(\mathbf<\frac<5><10>>\).
Десятичной дроби 1,3 соответствует смешанное число \(\mathbf<1\frac<3><10>>\).
Так как знаменатель полученных нами обыкновенных дробей равен десяти, разобьем единичный отрезок на десять равных частей (долей), каждая такая часть будет равна \(\mathbf<\frac<1><10>>\) (одной десятой) единичного отрезка ОЕ.
1. Правильная дробь \(\mathbf<\frac<5><10>>\)- это часть единичного отрезка, представляет собой 5 частей из десяти.
Отметим точку А(\(\mathbf<\frac<5><10>>\)) на координатном луче, для этого отсчитаем от начала координат пять частей (долей) единичного отрезка.
Так как \(\mathbf<\frac<5><10>>\) и 0,5— это одно и тоже число, следовательно, А(\(\mathbf<\frac<5><10>>\)) и А(0,5)- это одна и та же точка на координатном луче.
Обозначим на координатном луче точку В с координатой \(\mathbf<1\frac<3><10>>\).
Чтобы изобразить смешанное число \(\mathbf<1\frac<3><10>>\) отсчитаем от начала координат один целый единичный отрезок, а от второго единичного отрезка возьмем только три доли из десяти.
Отметим точку В(\(\mathbf<1\frac<3><10>>\)) на координатном луче.
Смешанное число и соответствующая ему неправильная дробь принадлежат одной точке координатного луча.
Переведем смешанное число \(\mathbf<1\frac<3><10>>\) в неправильную дробь, получим:
Так, если отсчитать от начала координат 13 частей единичного отрезка, каждый из которых равен \(\mathbf<\frac<1><10>>\) отрезка ОЕ, то в результате окажемся в точке с координатой \(\mathbf<\frac<13><10>>\).
В этой же точке мы ранее отметили точку В(\(\mathbf<1\frac<3><10>>\)).
Следовательно, точка с координатой 1,3, точка с координатой \(\mathbf<1\frac<3><10>>\) и точка с координатой \(\mathbf<\frac<13><10>>\)- это одна и та же точка на координатном луче.
В десятичной дроби справа от запятой после самой последней цифры, неравной нулю, можно приписывать сколько угодно нулей, в результате чего значение десятичной дроби не изменяется.
Например, 0,2 = 0,20
Равные десятичные дроби на координатном луче изображаются одной и той же точкой.
Точка с координатой 0,2 и точка с координатой 0,20— это одна и та же точка на координатном луче.
Меньшая десятичная дробь на координатном луче располагается левее, большая- правее.
Рассмотрим, как относительно друг друга на координатном луче расположены точки С(0,2), D(0,5), K(0,7).
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
По условию нам даны десятичные дроби с одним десятичным разрядом, следовательно, соответствующие им обыкновенные дроби, содержат в знаменателе число 10.
Так как знаменатель полученных нами обыкновенных дробей равен десяти, разобьем единичный отрезок на десять равных частей (долей), каждая такая часть будет равна \(\mathbf<\frac<1><10>>\) (одной десятой) единичного отрезка ОЕ.
Десятичной дроби 0,2 соответствует обыкновенная правильная дробь \(\mathbf<\frac<2><10>>\).
Дробь \(\mathbf<\frac<2><10>>\)- это часть единичного отрезка, представляет собой 2 части из десяти (две доли единичного отрезка ОЕ).
Десятичной дроби 0,5 соответствует обыкновенная правильная дробь \(\mathbf<\frac<5><10>>\).
Дробь \(\mathbf<\frac<5><10>>\) представляет собой 5 частей из десяти (пять долей единичного отрезка ОЕ).
Десятичной дроби 0,7 соответствует обыкновенная правильная дробь \(\mathbf<\frac<7><10>>\).
Дробь \(\mathbf<\frac<7><10>>\)- это часть единичного отрезка, представляет собой 7 частей из десяти (семь долей единичного отрезка ОЕ).
Точка С с координатой 0,2 лежит левее точки D(0,5) и точки K(0,7), следовательно, десятичная дробь 0,2 меньше десятичных дробей 0,5 и 0,7.
Точка D с координатой 0,5 лежит правее точки С(0,2) и левее точки K(0,7), следовательно, десятичная дробь 0,5 больше 0,2 и меньше 0,7.
Пройти тест и получить оценку можно после входа или регистрации
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Правильное округление чисел
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
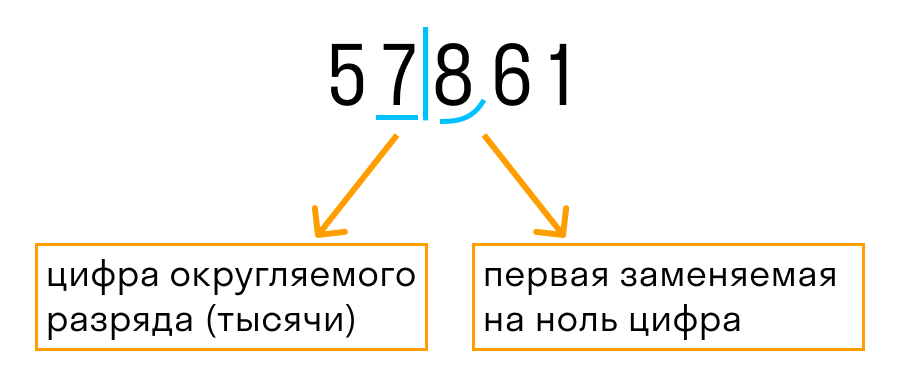
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
Разряды дробной части:
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
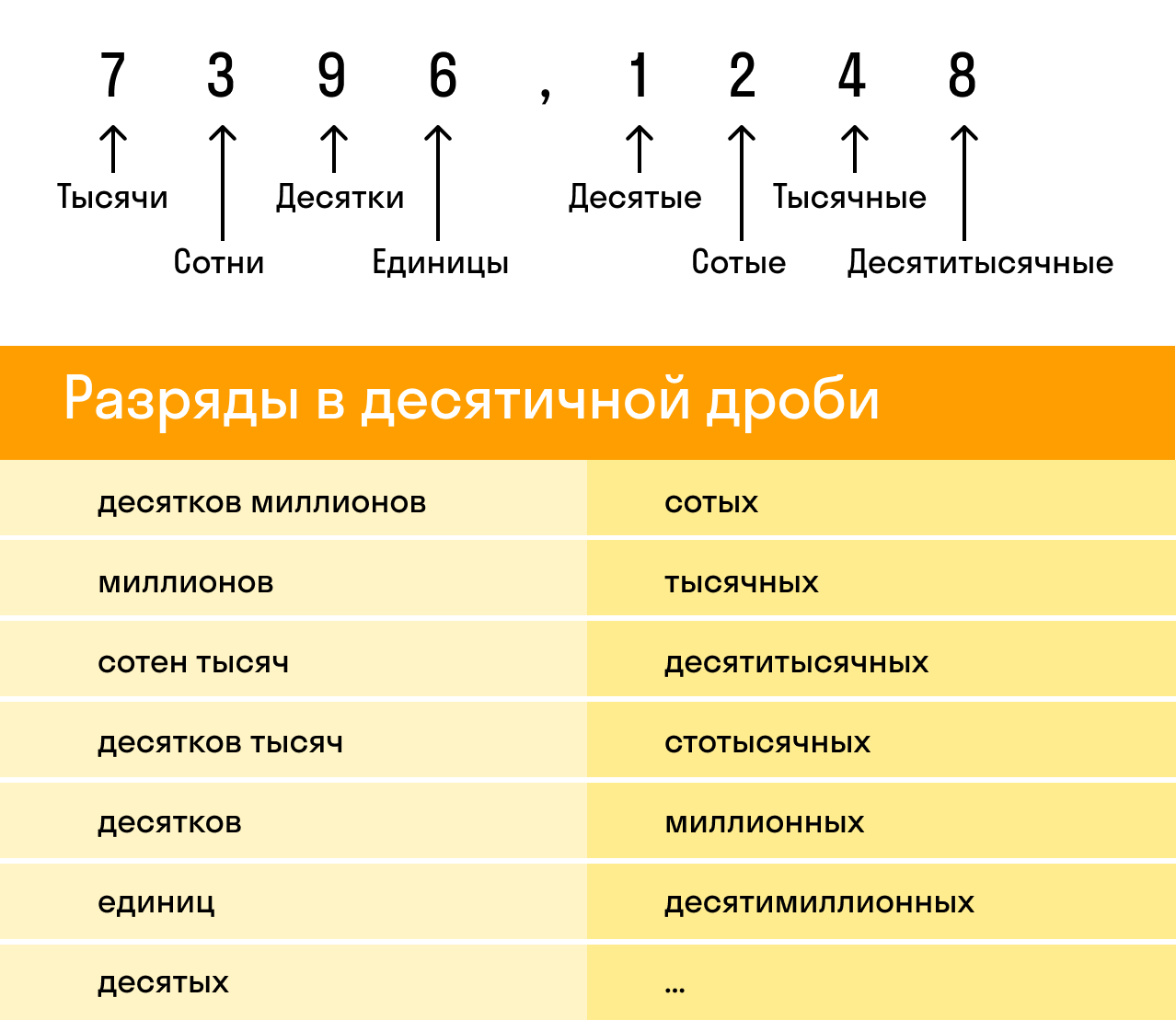
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.