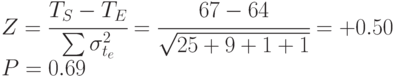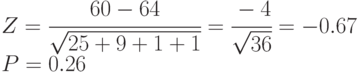для вычисления вероятности z необходимы такие данные как продолжительность критического пути
Метод критического пути в EXCEL
history 2 декабря 2017 г.
Метод критического пути (Critical Path Method) позволяет вычислить наиболее длительную последовательность работ, необходимую для завершения проекта в целом. Увеличение длительности любой из работ, лежащих на критическом пути приводит к увеличению длительности проекта. Работы, которые не лежат на критическом пути имеют определенный запас времени.
Постановка задачи
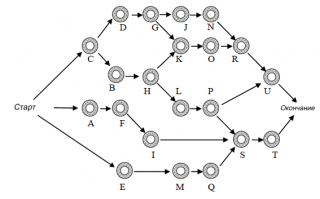
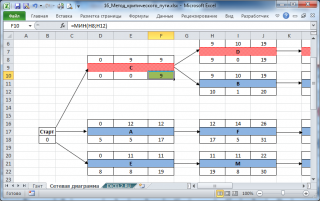
Пусть у нас есть проект, который состоит из 21 работы. Работы обозначены латинскими буквами и связаны друг с другом следующим образом:
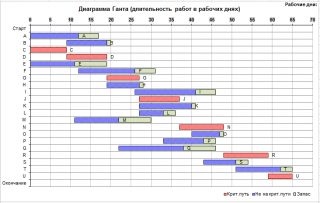
Диаграмма отображает длительности и взаимное расположение работ на шкале времени, а также критический путь. К сожалению, в отличие от MS Project, на диаграмме нельзя нарисовать стрелки, соединяющие работы.
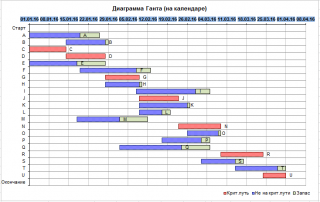
Также обратите внимание, что на диаграмме выше шкала времени представляет собой рабочие дни, т.к. длительности работ заданы в рабочих днях. Чтобы отобразить работы в календаре необходимо учесть выходные дни.
Исходные данные
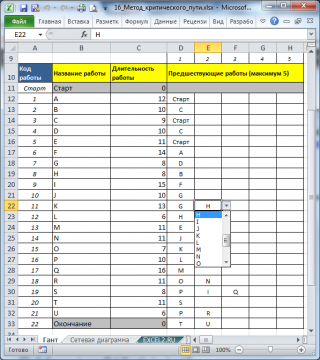
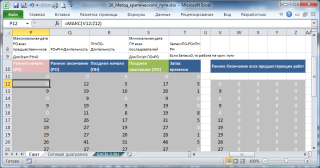
В файле примера заполнена таблица, содержащая перечень работ, их длительности и связи между работами.
Каждая работа имеет Название (для предотвращения загромождения текстом диаграммы здесь использованы латинские буквы от A до U) и код, который представляет собой последовательные числа от 1 до 21. Две работы не имеют длительности: Старт и Окончание.
Все остальные вычисления будут сделаны на основании этих данных.
Вычисление критического пути с помощью сетевой диаграммы
Для этого каждую работу представим в виде таблички:
Название работы выведем в таблички с помощью ссылок на лист с исходными данными. Длительность можно получить с помощью формулы =ВПР(D9;Гант!$B$12:$C$32;2;0)
Сначала вычислим Раннее Начало и Раннее Окончание двигаясь от вехи Старт до вехи Окончание (прямой проход). Затем вычислим Позднее начало и Позднее окончание двигаясь от вехи Окончание до вехи Старт (обратный проход).
На сетевой диаграмме сначала нарисуем веху Старт, ее длительность =0, и пусть она выполняется в день 0 (для удобства расчетов). Далее нарисуем вехи С, А, Е и их последователей: соответственно, D и E, F, M. Рассчитаем Раннее начало для этих и последующих работ:
С помощью Условного форматирования выделим те работы, у которых Запас =0. Это критический путь.
Примечание : В статье Автоматическая сетевая диаграмма проекта с критическим путем в MS EXCEL показано как построить Сетевую диаграмму не на отдельном листе, а на диаграмме MS EXCEL. Это позволяет автоматически перестраивать сетевую диаграмму при изменении связей между работами.
Очевидно, что использование Сетевой диаграммы неудобно для расчетов критического пути (но очень наглядно), поэтому для диаграммы Ганта рассчитаем критический путь с помощью тех же формул, но организованных несколько другим образом.
Построение диаграммы Ганта
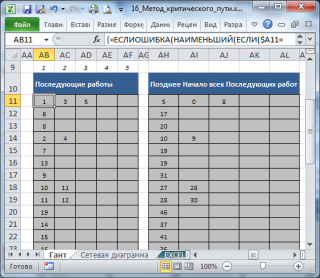
Для позднего окончания нам придется вычислить для каждой работы все ее Последующие работы. Это можно сделать из информации о предшествующих работах с помощью формулы массива :
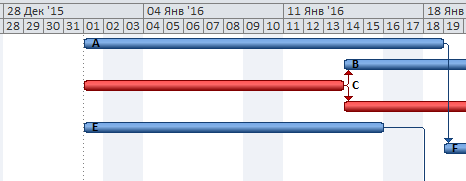
На основании вычисленных дат и диаграммы Линейчатая с накоплением создадим диаграмму Ганта.
Обратите внимание, что работы начинаются с 0:00 первого дня. Например, значение 5 на горизонтальной оси диаграммы означает, что прошло ровно 5 дней: с 0:00 первого дня до 23:59 четвертого дня. Этот подход отличается от принятого в MS Project, где длительность работ отображается более наглядно:
Примечание : Все расчеты сверены с MS Project (длительность проекта, вычисление критического пути, сроки начала и завершения работ).
Управление риском
PERT и PERT-моделирование
В 1958 г. Особый отдел Военно-морского флота и консалтинговая фирма Booze, Allen and Hamilton создали PERT (метод оценки и проверки программ) с целью разработки графика для более чем 3300 подрядчиков, работающих над проектом подводной лодки Поларис, для решения проблемы неопределенности в расчетах времени выполнения работ.
PERT почти полностью совпадает с методом критического пути (СРМ), за исключением того, что PERT считает, что продолжительность каждой операции имеет пределы, которые исходят из статистического распределения.
PERT использует 3 оценки расчета времени для каждой операции:
Разработчики PERT для выражения продолжительности операции решили избрать аппроксимацию бета-распределения.
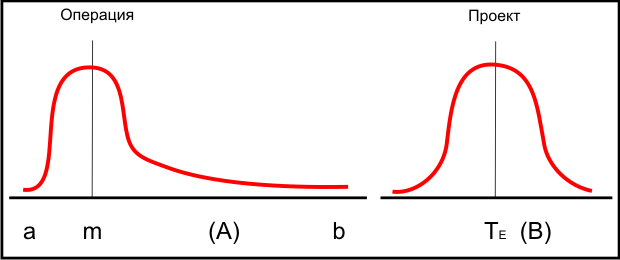
На рис. 5.2(А) представлено бета-распределение для продолжительности операции, отклоняющееся вправо, и оно представляет собой работу, которая имеет тенденцию отставать от графика.
Распределение продолжительности проекта показано в симметрии на рис. 5-2 (В).
Средневзвешенное время операции рассчитывается по следующей формуле:
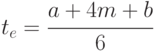 | ( 5.1) |
Среднее (детерминистическое) значение накладывают на сеть проекта, как и при использовании СРМ, и затем рассчитывают раннее, позднее, резервное и время завершения проектных работ, как они указаны в СРМ.
Отклонения в оценках времени операции определяются при помощи следующих уравнений. Уравнение 5.2 представляет стандартное отклонение для операции.
 | ( 5.2) |
 | ( 5.3) |
Уравнение 5.3 представляет стандартное отклонение для проекта.
Эта сумма включает в себя только виды операций на критическом или проверенном пути.
Зная среднюю продолжительность проекта и дисперсии (среднего отклонения) операций, можно с помощью статистических таблиц рассчитать выполнение проекта (или сегмента проекта) к конкретному времени.
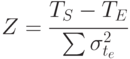 | ( 5.4) |
Гипотетический пример использования метода PERT
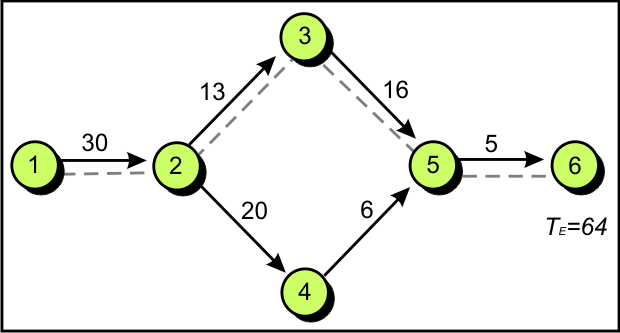
Продолжительность операций и значение среднего отклонения представлены на табл. 5.5.
| Операция | a | m | b | ТЕ | квадрат среднего отклонения |
|---|---|---|---|---|---|
| 1-2 | 17 | 29 | 47 | 30 | 25 |
| 2-3 | 6 | 12 | 24 | 13 | 9 |
| 2-4 | 16 | 19 | 28 | 20 | 4 |
| 3-5 | 13 | 16 | 19 | 16 | 1 |
| 4-5 | 2 | 5 | 14 | 6 | 4 |
| 5-6 | 2 | 5 | 8 | 5 | 1 |
Сеть проекта представлена на рис. 5.3.
Прогнозируемый срок работы ( ТЕ ) представлен 64 единицами времени;
Например, какова вероятность завершения работы над проектом до указанного в графике времени ( Ts ) из 67?
Обычная кривая проекта будет такой как на рис. 5.4
| Величина Z | Вероятность | Величина Z | Вероятность |
|---|---|---|---|
| -2,0 | 0,02 | +2,0 | 0,98 |
| -1,5 | 0,07 | + 1,5 | 0,93 |
| -1,0 | 0,16 | +1,0 | 0,84 |
| -0,7 | 0,24 | +0,7 | 0,76 |
| -0,5 | 0,31 | +0,5 | 0,69 |
| -0.3 | 0,38 | +0,3 | 0,62 |
| -0,1 | 0,36 | +0,1 | 0,54 |
Вероятность выполнения проекта к периоду времени 60 рассчитывается следующим образом:
Аналогичный способ расчетов можно использовать для любого пути или участка пути в сети.
PERT-моделирование
Для этой методики необходима компьютерная программа, моделирующая отпущенные на проект время, затраты и/или наличие ресурсов с использованием метода Monte Carlo Technique.
Решения по сохранению или переадресации рисков принимаются с помощью информации, полученной в результате моделирования времени, затрат и ресурсов.
Управление риском
PERT и PERT-моделирование
В 1958 г. Особый отдел Военно-морского флота и консалтинговая фирма Booze, Allen and Hamilton создали PERT (метод оценки и проверки программ) с целью разработки графика для более чем 3300 подрядчиков, работающих над проектом подводной лодки Поларис, для решения проблемы неопределенности в расчетах времени выполнения работ.
PERT почти полностью совпадает с методом критического пути (СРМ), за исключением того, что PERT считает, что продолжительность каждой операции имеет пределы, которые исходят из статистического распределения.
PERT использует 3 оценки расчета времени для каждой операции:
Разработчики PERT для выражения продолжительности операции решили избрать аппроксимацию бета-распределения.
На рис. 5.2(А) представлено бета-распределение для продолжительности операции, отклоняющееся вправо, и оно представляет собой работу, которая имеет тенденцию отставать от графика.
Распределение продолжительности проекта показано в симметрии на рис. 5-2 (В).
Средневзвешенное время операции рассчитывается по следующей формуле:
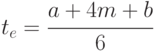 | ( 5.1) |
Среднее (детерминистическое) значение накладывают на сеть проекта, как и при использовании СРМ, и затем рассчитывают раннее, позднее, резервное и время завершения проектных работ, как они указаны в СРМ.
Отклонения в оценках времени операции определяются при помощи следующих уравнений. Уравнение 5.2 представляет стандартное отклонение для операции.
 | ( 5.2) |
 | ( 5.3) |
Уравнение 5.3 представляет стандартное отклонение для проекта.
Эта сумма включает в себя только виды операций на критическом или проверенном пути.
Зная среднюю продолжительность проекта и дисперсии (среднего отклонения) операций, можно с помощью статистических таблиц рассчитать выполнение проекта (или сегмента проекта) к конкретному времени.
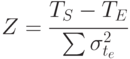 | ( 5.4) |
Гипотетический пример использования метода PERT
Продолжительность операций и значение среднего отклонения представлены на табл. 5.5.
| Операция | a | m | b | ТЕ | квадрат среднего отклонения |
|---|---|---|---|---|---|
| 1-2 | 17 | 29 | 47 | 30 | 25 |
| 2-3 | 6 | 12 | 24 | 13 | 9 |
| 2-4 | 16 | 19 | 28 | 20 | 4 |
| 3-5 | 13 | 16 | 19 | 16 | 1 |
| 4-5 | 2 | 5 | 14 | 6 | 4 |
| 5-6 | 2 | 5 | 8 | 5 | 1 |
Сеть проекта представлена на рис. 5.3.
Прогнозируемый срок работы ( ТЕ ) представлен 64 единицами времени;
Например, какова вероятность завершения работы над проектом до указанного в графике времени ( Ts ) из 67?
Обычная кривая проекта будет такой как на рис. 5.4
| Величина Z | Вероятность | Величина Z | Вероятность |
|---|---|---|---|
| -2,0 | 0,02 | +2,0 | 0,98 |
| -1,5 | 0,07 | + 1,5 | 0,93 |
| -1,0 | 0,16 | +1,0 | 0,84 |
| -0,7 | 0,24 | +0,7 | 0,76 |
| -0,5 | 0,31 | +0,5 | 0,69 |
| -0.3 | 0,38 | +0,3 | 0,62 |
| -0,1 | 0,36 | +0,1 | 0,54 |
Вероятность выполнения проекта к периоду времени 60 рассчитывается следующим образом:
Аналогичный способ расчетов можно использовать для любого пути или участка пути в сети.
PERT-моделирование
Для этой методики необходима компьютерная программа, моделирующая отпущенные на проект время, затраты и/или наличие ресурсов с использованием метода Monte Carlo Technique.
Решения по сохранению или переадресации рисков принимаются с помощью информации, полученной в результате моделирования времени, затрат и ресурсов.
Управление риском
PERT и PERT-моделирование
В 1958 г. Особый отдел Военно-морского флота и консалтинговая фирма Booze, Allen and Hamilton создали PERT (метод оценки и проверки программ) с целью разработки графика для более чем 3300 подрядчиков, работающих над проектом подводной лодки Поларис, для решения проблемы неопределенности в расчетах времени выполнения работ.
PERT почти полностью совпадает с методом критического пути (СРМ), за исключением того, что PERT считает, что продолжительность каждой операции имеет пределы, которые исходят из статистического распределения.
PERT использует 3 оценки расчета времени для каждой операции:
Разработчики PERT для выражения продолжительности операции решили избрать аппроксимацию бета-распределения.
На рис. 5.2(А) представлено бета-распределение для продолжительности операции, отклоняющееся вправо, и оно представляет собой работу, которая имеет тенденцию отставать от графика.
Распределение продолжительности проекта показано в симметрии на рис. 5-2 (В).
Средневзвешенное время операции рассчитывается по следующей формуле:
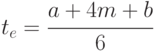 | ( 5.1) |
Среднее (детерминистическое) значение накладывают на сеть проекта, как и при использовании СРМ, и затем рассчитывают раннее, позднее, резервное и время завершения проектных работ, как они указаны в СРМ.
Отклонения в оценках времени операции определяются при помощи следующих уравнений. Уравнение 5.2 представляет стандартное отклонение для операции.
 | ( 5.2) |
 | ( 5.3) |
Уравнение 5.3 представляет стандартное отклонение для проекта.
Эта сумма включает в себя только виды операций на критическом или проверенном пути.
Зная среднюю продолжительность проекта и дисперсии (среднего отклонения) операций, можно с помощью статистических таблиц рассчитать выполнение проекта (или сегмента проекта) к конкретному времени.
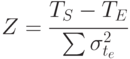 | ( 5.4) |
Гипотетический пример использования метода PERT
Продолжительность операций и значение среднего отклонения представлены на табл. 5.5.
| Операция | a | m | b | ТЕ | квадрат среднего отклонения |
|---|---|---|---|---|---|
| 1-2 | 17 | 29 | 47 | 30 | 25 |
| 2-3 | 6 | 12 | 24 | 13 | 9 |
| 2-4 | 16 | 19 | 28 | 20 | 4 |
| 3-5 | 13 | 16 | 19 | 16 | 1 |
| 4-5 | 2 | 5 | 14 | 6 | 4 |
| 5-6 | 2 | 5 | 8 | 5 | 1 |
Сеть проекта представлена на рис. 5.3.
Прогнозируемый срок работы ( ТЕ ) представлен 64 единицами времени;
Например, какова вероятность завершения работы над проектом до указанного в графике времени ( Ts ) из 67?
Обычная кривая проекта будет такой как на рис. 5.4
| Величина Z | Вероятность | Величина Z | Вероятность |
|---|---|---|---|
| -2,0 | 0,02 | +2,0 | 0,98 |
| -1,5 | 0,07 | + 1,5 | 0,93 |
| -1,0 | 0,16 | +1,0 | 0,84 |
| -0,7 | 0,24 | +0,7 | 0,76 |
| -0,5 | 0,31 | +0,5 | 0,69 |
| -0.3 | 0,38 | +0,3 | 0,62 |
| -0,1 | 0,36 | +0,1 | 0,54 |
Вероятность выполнения проекта к периоду времени 60 рассчитывается следующим образом:
Аналогичный способ расчетов можно использовать для любого пути или участка пути в сети.
PERT-моделирование
Для этой методики необходима компьютерная программа, моделирующая отпущенные на проект время, затраты и/или наличие ресурсов с использованием метода Monte Carlo Technique.
Решения по сохранению или переадресации рисков принимаются с помощью информации, полученной в результате моделирования времени, затрат и ресурсов.