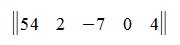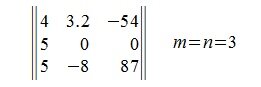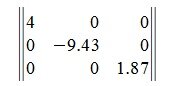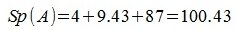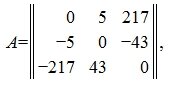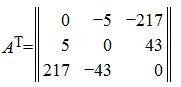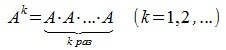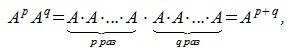единичная матрица это такая матрица в которой
Единичная матрица
Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.
Содержание
Определение
Квадратная матрица 
размера (порядка 
), где 
для всякого 
, и 
для всяких 
, называется единичной матрицей порядка .
Единичную матрицу можно определить как матрицу 
, у которой 
, где 
— символ Кронекера.
Единичная матрица является частным случаем скалярной матрицы.
Обозначение
Единичная матрица размера 
обычно обозначается 
и имеет вид:
Так же используется и другое обозначение: 
.
Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается: 
, 
.
Свойства
Примеры
Единичные матрицы первых порядков имеют вид
Замечание
Если взять две матрицы —: матрицу 
и единичную — то, приведением матрицы к единичной методом Гаусса, можно добиться одновременного приведения матрицы к матрице 
.
Литература
См. также
Полезное
Смотреть что такое «Единичная матрица» в других словарях:
единичная матрица — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] единичная матрица Такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу — единицы, а остальные… … Справочник технического переводчика
Единичная матрица — [unit matrix, identity matrix] такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу единицы, а остальные нули, например: Е.м. применяется в процессе обращения матриц, в … Экономико-математический словарь
единичная матрица — vienetinė matrica statusas T sritis fizika atitikmenys: angl. identity matrix; unit matrix vok. Einheitsmatrix, f rus. единичная матрица, f pranc. matrice unité, f; matrice unitaire, f … Fizikos terminų žodynas
Матрица — [matrix] система элементов (чисел, функций и других величин), расположенных в виде прямоугольной таблицы, над которой можно производить определенные действия. Таблица имеет следующий вид: Элемент матрицы в общем виде обозначается aij это… … Экономико-математический словарь
матрица — Логическая сеть, сконфигурированная в виде прямоугольного массива пересечений входных/выходных каналов. [http://www.vidimost.com/glossary.html] матрица Система элементов (чисел, функций и других величин), расположенных в виде прямоугольной… … Справочник технического переводчика
МАТРИЦА ПЛОТНОСТИ — (статистический оператор), оператор, при помощи к рого можно вычислить ср. значение любой физ. величины в квант. статистич. механике и, в частном случае, в квант. механике. Термин «М. п.» связан с тем, что статистич. оператор задаётся обычно в… … Физическая энциклопедия
Матрица (математика) — У этого термина существуют и другие значения, см. Матрица. Матрица математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), которая представляет… … Википедия
Матрица линейного оператора — Матрица математический объект, записываемый в виде прямоугольной таблицы чисел (или элементов кольца) и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами. Правила выполнения… … Википедия
Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия
Матрица Адамара — Для улучшения этой статьи желательно?: Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное. Матрица … Википедия
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
(i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
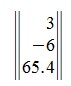
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Побочная диагональ матрицы
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
След матрицы
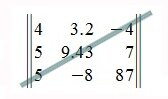
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
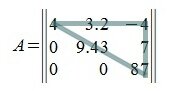
Верхняя треугольная матрица
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
Единичная матрица это такая матрица в которой
Трудно представить себе систему чисел, которая бы не содержала единичный элемент. В частности, именно единица является результатом умножения числа a на ему обратное. Алгебра любых объектов (вещественных или комплексных чисел, векторов и так далее) должна включать в себя единичный элемент. Не является исключением и матричная алгебра, в которой роль единицы играет диагональная матрица, все диагональные элементы которой равны единице.
В качестве определения единичной матрицы могло бы выступать примерно такое.
Матрица E называется единичной, если при умножении на нее любой матрицы A (слева и справа) матрица A остается неизменной: AE = EA = A.
Связано это с тем, что операция умножения определена не для любых матриц и, следовательно, требуется определенное согласование размеров иатриц-сомножителей. В результате под единичной матрицей понимается матрица вышеуказанной структуры, порядок которой выбирается таким, чтобы соответствующее произведение было определено.
), называется единичной матрицей и обозначается символом E. Элементы единичной матрицы могут быть представлены с помощью дельта-символа Кронекера:
 . | (1) |
В матричной алгебре матрица E играет ту же роль, что число единица в системе вещественных чисел, а именно – при умножении на единичную матрицу (справа или слева) исходная матрица не изменяется:
Рассмотрим теперь i,j-ый элемент матричного произведения EA, где E – единичная матрица m-го порядка:
Математика для чайников. Матрицы и основные действия над ними
Определение матрицы
Матрица – это прямоугольная таблица элементов. Ну а если простым языком – таблица чисел.
Обычно матрицы обозначаются прописными латинскими буквами. Например, матрица A, матрица B и так далее. Матрицы могут быть разного размера: прямоугольные, квадратные, также есть матрицы-строки и матрицы-столбцы, называемые векторами. Размер матрицы определяется количеством строк и столбцов. Например, запишем прямоугольную матрицу размера m на n, где m – количество строк, а n – количество столбцов.
Что можно делать с матрицами? Складывать/вычитать, умножать на число, умножать между собой, транспонировать. Теперь обо всех этих основных операциях над матрицами по порядку.
Операции сложения и вычитания матриц
Сразу предупредим, что можно складывать только матрицы одинакового размера. В результате получится матрица того же размера. Складывать (или вычитать) матрицы просто – достаточно только сложить их соответствующие элементы. Приведем пример. Выполним сложение двух матриц A и В размером два на два.
Вычитание выполняется по аналогии, только с противоположным знаком.
Умножение матрицы на число
На произвольное число можно умножить любую матрицу. Чтобы сделать это, нужно умножить на это число каждый ее элемент. Например, умножим матрицу A из первого примера на число 5:
Операция умножения матриц
И пример с реальными числами. Умножим матрицы:
Операция транспонирования матрицы
Транспонирование матрицы – это операция, когда соответствующие строки и столбцы меняются местами. Например, транспонируем матрицу A из первого примера:
Определитель матрицы
Определитель, о же детерминант – одно из основных понятий линейной алгебры. Когда-то люди придумали линейные уравнения, а за ними пришлось выдумать и определитель. В итоге, разбираться со всем этим предстоит вам, так что, последний рывок!
Определитель – это численная характеристика квадратной матрицы, которая нужна для решения многих задач.
Чтобы посчитать определитель самой простой квадратной матрицы, нужно вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка, то есть состоящей из одного элемента, равен этому элементу.
А если матрица три на три? Тут уже посложнее, но справиться можно.
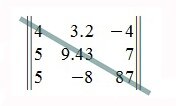
Для такой матрицы значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.
К счастью, вычислять определители матриц больших размеров на практике приходится редко.
Единичная матрица это такая матрица в которой
Матрицей 
размерности m×n называется таблица чисел aij, содержащая m строк и n столбцов. Числа aij называются элементами этой матрицы, где i – номер строки, j – номер столбца, на пересечении которых стоит данный элемент. Матрица, содержащая m строк и n столбцов, имеет вид:
Виды матриц:
1) при m=n – квадратная, в данном случае n называют порядком матрицы;
2) квадратная матрица, у которой все недиагональные элементы равны нулю – диагональная;
3) диагональная матрица, у которой все диагональные элементы равны единице – единичная и обозначается E;
4) при n≠m – прямоугольная;
5) при m=1 – матрица-строка (вектор-строка);
6) при n=1 – матрица-столбец (вектор-столбец);
7) при всех aij =0 – нулевая матрица.
Заметим, что основной числовой характеристикой квадратной матрицы является ее определитель. Определитель, соответствующий матрице n-го по-порядка, также имеет n-ый порядок.
Дадим ряд необходимых определений.
Определителем матрицы 2-го порядка называется число
Минором Мij элемента aij матрицы n-го порядка А называется определитель матрицы (n-1)-го порядка, полученной из матрицы А путем вычеркивания i-ой строки и j-го столбца.
1. При транспонировании матрицы ее определитель не меняется.
2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак.
3. Определитель, имеющий две пропорциональные (равные) строки (столбца), равен нулю.
4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.
5. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), предварительно умноженные на любое число.
7. Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.
Поясним данное свойство на примере определителя 3-го порядка. В данном случае свойство 7 означает, что
Свойство 7 представляет собой теорему о разложении определителя, сформулированную Лапласом.
8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.
Последнее свойство часто называют псевдоразложением определителя.