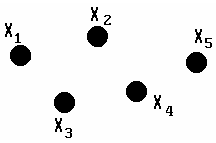если две различные вершины графа соединены более чем одним ребром то такие ребра называются
Характеристики графа
Теорема 1. Если конечный граф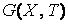 
(без петель) имеет
n вершин и m ребер, то
Теорема 2. Число нечетных вершин любого графа четно.
Теорема 3. Во всяком графе с n вершинами ( n >2) всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.
Путь и ци кл в гр афе
Циклом называется путь, в котором начальная и конечная вершины совпадают. Длиной цикла называется число ребер в этом цикле. Цикл называется простым, если он не проходит через одну вершину более одного раза.
Теорема 5. Если у графа 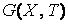все простые циклы четной длины, то граф не имеет ни одного цикла нечетной длины.
Связность графа, деревья
Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах, и несвязными в противном случае. Граф называется связным, если любые две его вершины связны, и несвязным в противном случае.
Теорема 6. Связный граф 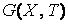представляет собой простой цикл тогда и только тогда, когда каждая его вершина имеет степень 2.
Связный граф без циклов называется деревом. Вершина дерева, имеющая степень 1, называется висячей.
Плоские графы
Граф 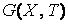называется плоским, если его можно изобразить на плоскости так, чтобы никакие два его ребра не имели других общих точек, кроме их общей вершины. Чертеж графа, на котором никакие два ребра не пересекаются, называют плоским представлением графа.
Плоское представление имеет только плоский граф, и обратно: у всякого плоского графа всегда найдется плоское представление.
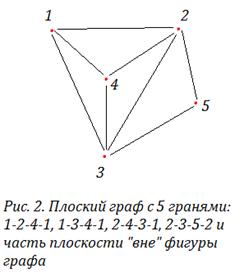
Гранью в плоском представлении графа 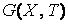наз ывают часть плоскости, ограниченную простым циклом и не содержащую внутри других циклов. Часть плоскости, расположенная вне плоского представления графа и ограниченная изнутри простым циклом, называется бесконечной гранью. Две грани называются соседними, если их границы имеют хотя бы одно общее ребро. Мост, соединяющий два цикла, называется перегородкой.
В плоском представлении дерева за грань принимают всю плоскость чертежа.
которое называется формулой Эйлера.
Операция добавления новых ребер, в результате которой в плоском представлении графа каждая грань имеет ровно три вершины, называется триангуляцией графа.
Эйлеровы графы
Эйлеровым путем в графе называют путь, содержащий все ребра графа и проходящий через каждое по одному разу. Эйлеровым циклом в графе называют цикл, содержащий все ребра графа и проходящий через каждое по одному разу. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Теорема 9. Если граф 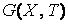связный и все его вершины четны, то он обладает эйлеровым циклом.
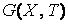
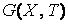
Теорема 10. Если граф обладает эйлеровым путем с концами А и В, то граф связн ый и А и В его единственные нечетные вершины.
Теорема 11. Если граф 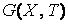связный и А и В его единственные нечетные вершины, то граф обладает эйлеровым путем с концами А и В.
Теорема 12. Если граф 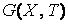связный, то можно построить цикличный маршрут, содержащий в се ребра в точности два раза, по одному в каждом направлении.
Гамильтоновы графы
Гамильтоновым путем в графе называют путь, проходящий через каждую вершину графа в точности по одному разу. Гамильтоновым циклом в графе называют цикл, проходящий через каждую вершину графа в точности по одному разу. Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.
Теорема 13. Граф с m вершинами имеет гамильтонов цикл, если для любой его вершины Ai
Ориентированные графы
Теорема 14. Всякий полный ориентированный граф имеет путь, проходящий через все вершины.
Граф (теория графов)
В математической теории графов и информатике граф — это совокупность объектов со связями между ними.
Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.
Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами. Например, строение Википедии можно смоделировать при помощи ориентированного графа (орграф), в котором вершины — это статьи, а дуги (ориентированные рёбра) — это связи, созданные гиперссылками (см. Тематическая карта).
Содержание
Определения
Теория графов не обладает устоявшейся терминологией. В различных статьях под одними и теми же терминами понимаются разные вещи. Приводимые ниже определения — наиболее часто встречаемые.
V (а значит и E ) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становятся ложными в случае бесконечных множеств.
Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа.
Два ребра называются смежными, если они имеют общую концевую вершину.
Два ребра называются кратными, если множества их концевых вершин совпадают.
Степенью degV вершины V называют количество рёбер, для которых она является концевой (при этом петли считают дважды).
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Ориентированный граф
Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга v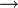 
w ведёт от вершины v к вершине w.
Смешанный граф
Понятно, что ориентированный и неориентированный графы являются частными случаями смешанного.
Прочие связанные определения
Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром.
Ориентированным путём в орграфе называют конечную последовательность вершин vi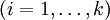 
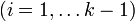
, для которой все пары (vi,vi + 1) 
являются (ориентированными) рёбрами.
Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u и v являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u) является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что:
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u в v », является отношением эквивалентности, и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G называется связной компонентой (или просто компонентой) графа G. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Способы представления графа в информатике
Матрица смежности
Матрица смежности — таблица, где как столбцы, так и строки соответствуют вершинам графа. В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Недостатком являются требования к памяти — очевидно, квадрат количества вершин.
Матрица инцидентности
Данный способ является самым ёмким (размер пропорционален | E | | V | ) и неудобным для хранения, но облегчает нахождение циклов в графе.
Список рёбер
Список рёбер — это тип представления графа в памяти, подразумевающий, что каждое ребро представляется двумя числами — номерами вершин этого ребра. Список рёбер более удобен для реализации различных алгоритмов на графах по сравнению с матрицей смежности.
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку 
, где V и E — некоторые множества (вершин и рёбер, соотв.), а 
— функция инцидентности (или инцидентор), сопоставляющая каждому ребру 
(упорядоченную или неупорядоченную) пару вершин u и v из V (его концов). Частными случаями этого понятия являются:
Под данное выше определение не подходят некоторые другие обобщения:
Литература
См. также
Ссылки
Популярные программы для визуализации графов
Элементы теории графов
Ищем педагогов в команду «Инфоурок»
Описание презентации по отдельным слайдам:
Описание слайда:
Элементы теории графов
Описание слайда:
Содержание
1. Основные понятия теории графов
2. Степень вершины
Введение
5. Ориентированные графы
6. Изоморфизм графов
7. Плоские графы
8. Операции над графами
9. Способы задания графов
3. Маршруты, цепи, циклы
10. Некоторые типы графов
Описание слайда:
Введение
Теория графов в качестве дисциплины может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами (изучение объектов).
Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.
Особенно широкое применение теории графов в таких областях прикладной математики, как программирование, теория конечных автоматов, в решении вероятностных и комбинаторных задач.
Описание слайда:
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром.
Описание слайда:
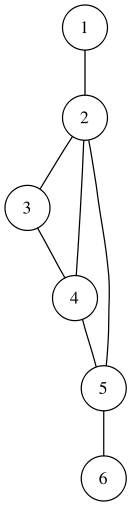
Степенью вершины называется число ребер графа, которым принадлежит эта вершина. Еще называют его валентностью и обозначают d(v), deg(v). Вершина графа, для которой d(v)=0, является изолированной, если d(v)=1, то висячей.
Deg(6)=3, deg(5)=1, 5 – висячая вершина
N(3)=<2,1,6,4>, deg(7)=0, 7 – изолированная вершина
Вершина называется нечетной, если d(v) – нечетное число, четной если d(v) – четное число. Степень каждой вершины полного графа на единицу меньше числа его вершин.
Рис 2.1
2. Степень вершины
Описание слайда:
В графе G(V,E) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа.
Число нечетных вершин любого графа четно.
Во всяком графе с n вершинами, где n ≥ 2 всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.
Если в графе с n вершинами (n ≥ 2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени n-1.
Свойства степени вершины
Описание слайда:
Маршрутом в графе называется чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны:
Описание слайда:
Две вершины графа называются связными, если существует соединяющая их простая цепь. В противном случае две вершины называются не связными.
Граф называется связным, если каждые две вершины связные.
Граф называется несвязным, если хотя бы две его вершины несвязные.
Описание слайда:
Если элементы множества Е графа G(V, E) – упорядоченные пары, то граф называется ориентированным или орграфом.
Ребро графа называется ориентированным, если одну вершину ребра считают началом ребра а другую концом, на рисунке изображают стрелкой между вершинами. Граф у которого все ребра ориентированы – ориентированный.
Ориентированное ребро
Неориентированное ребро
Одна и та же вершина ориентированного графа может служить началом для одних ребер и концом для других, поэтому различают две степени вершины:
Степенью выхода вершины орграфа – число выходящих из вершины ребер;
Степенью входа вершины орграфа – число входящих в вершину ребер.
Рис 5.1
Рис 5.2
5. Ориентированные графы
Описание слайда:
В орграфах в зависимости от сочетания степеней входа и выхода для данной вершины рассматриваются три случая:
Изолированной вершиной называется вершина у которой степень входа и степень выхода равны 0;
Источником называется вершина, степень выхода которой положительна, а степень входа равна 0;
Стоком называется вершина, степень входа которой положительна, а степень выхода равна 0.
Путем в ориентированном графе называется последовательность ориентированных ребер.
Простым путем в ориентированном графе называется путь, в котором ни одна вершина не содержится более одного раза (Рис 5.3). На рис 5.4 изображен не простой путь.
Рис 5.3
Рис 5.4
Описание слайда:
Петлей называется ребро, у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной.
Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами. Для ориентированного мультиграфа вершины могут соединятся несколькими ребрами в каждом из направлений.
Замкнутый путь в ориентированном графе называется ориентированным циклом или контуром. Длиной пути называется число ребер в этом пути.
Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром. Если ребра полного графа неориентированные, то граф соответственно будет полным неориентированным.
Ориентированный граф
Описание слайда:
Описание слайда:
Описание слайда:
Пример «Изоморфизма графов»
Описание слайда:
7. Плоские графы
Граф называется плоским, если на плоскости его можно изобразить так, чтобы все пересечения его ребер являются вершинами графа
В качестве характеристики плоского представления графа вводится понятие грани (рис 7.1). Грань в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.
Рис 7.1
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
10. Некоторые типы графов
Эйлеровы графы
Эйлеровым путем в графе называется путь, содержащий все ребра графа.
Эйлеровым циклом или эйлеровой цепью называется цикл, содержащий все ребра графа и притом по одному разу. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Замкнутую линию, если ее можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз, принято называть уникурсальной. Рисунок графа, обладающего эйлеровым путем или циклом, является уникурсальной линией.
Теорема 1. Если граф G(V,E) обладает эйлеровым циклом, то он связный и все его вершины четные.
Теорема 2. Если граф G(V,E) связный и все его вершины четные, то он обладает эйлеровым циклом.
Описание слайда:
Гамильтоновы графы
Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом. Гамильтоновым циклом, называется цикл, или путь, проходящий через каждую вершину графа в точности по одному разу.
Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все ребра, и притом по одному разу, вторые – все вершины по одному разу. Для решения вопроса о существовании эйлерова цикла в графе достаточно выяснить, все ли его вершины четные.
Условия существования гамильтоновых циклов
Всякий полный граф является гамильтоновым, так как содержит простой цикл, которому принадлежат все вершины данного графа.
Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.
Если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы.
Описание слайда:
Спасибо за внимание!
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ГРАФОВ
Теория графов, как было сказано выше – дисциплина математическая, созданная усилиями математиков, поэтому ее изложение включает в себя и необходимые строгие определения. Итак, приступим к организованному введению основных понятий этой теории.
Определение 2.01. Графом называется совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.
Это определение можно сформулировать иначе: графомназывается непустое множество точек (вершин) и отрезков (ребер), оба конца которых принадлежат заданному множеству точек (см. рис. 2.1).
В дальнейшем вершины графа мы будем обозначать латинскими буквами A, B, C, D. Иногда граф в целом будем обозначать одной заглавной буквой.
Определение 2.02.Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.
Определение 2.03.Граф, состоящий только из изолированных вершин, называется нуль—графом.
Обозначение: O’– граф с вершинами, не имеющий ребер (рис. 2.2).
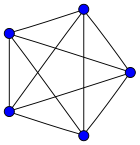
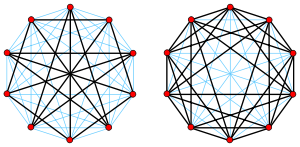
Определение 2.04.Граф, в котором каждая пара вершин соединена ребром, называется полным.
Обозначение: U’–граф, состоящий из n вершин и ребер, соединяющих всевозможные пары этих вершин. Такой граф можно представить как n–угольник, в котором проведены все диагонали (рис. 2.3).
Определение 2.05.Степеньювершиныназывается число ребер, которым принадлежит вершина.
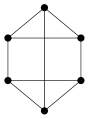
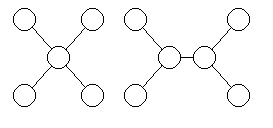
Определение 2.06.Граф, степени всех k вершин которого одинаковы, называется однороднымграфомстепениk.
На рисунке 2.4 и 2.5 изображены однородные графы второй и третьей степени.
Определение 2.07.Дополнениемданногографаназывается граф, состоящий из всех ребер и их концов, которые необходимо добавить к исходному графу, чтобы получить полный граф.
На рисунке 2.6 изображен исходный граф G, а на рисунке 2.7 – дополнение данного графа – граф G’.
Определение 2.08.Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским. (рис. 2.8)
Определение 2.09.Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер графа, называют его гранью.
Понятия плоского графа и грани графа применяется при решении задач на «правильное» раскрашивание различных карт.
Определение 2.10.Путемот AдоXназывается последовательность ребер, ведущая от A к X, такая, что каждые два соседних ребра имеют общую вершину, и никакое ребро не встречается более одного раза.
Определение 2.11.Цикломназывается путь, в котором совпадают начальная и конечная точка.
Определение 2.12.Простым цикломназывается цикл, не проходящий ни через одну из вершин графа более одного раза.
Определение 2.13.Длиной пути,проложенного на цикле,называется число ребер этого пути.
Определение 2.14.Две вершины A и Bв графе называются связными(несвязными), если в нем существует (не существует) путь, ведущий из A в B.
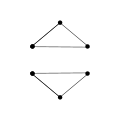
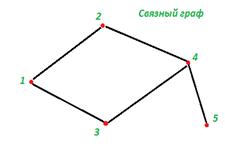
Определение 2.15.Граф называется связным, если каждые две его вершины связны; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.
На рисунке 2.9 изображен связный граф; на рисунке 2.10 – несвязный (т. к. существует минимум одна пара несвязных вершин – A и D).
Определение 2.16.Деревомназывается связный граф, не содержащий циклов.
Трехмерной моделью графа-дерева служит, например, настоящее дерево с его замысловато разветвленной кроной; река и ее притоки также образуют дерево, но уже плоское – на поверхности земли
Определение 2.17.Несвязный граф, состоящий исключительно из деревьев, называется лесом.
Определение 2.13.Дерево, все n вершин которого имеют номера от 1 до n, называют деревом с перенумерованными вершинами.
Итак, мы рассмотрели основные определения теории графов, без которых было бы невозможно доказательство теорем, а следовательно и решение задач. Формулировки и доказательства ключевых теорем будут приведены ниже, в этом же параграфе объяснены базовые понятия теории.