Игральный кубик бросают дважды найдите вероятность того что первый раз выпадет 6
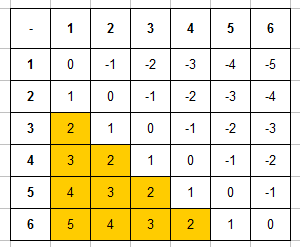
Игральный кубик бросают дважды найдите вероятность того что первый раз выпадет 6
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, большее 3.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет больше трёх очков» удовлетворяют три случая: когда на кубике выпадает 4, 5, или 6 очков. Поэтому вероятность того, что на кубике выпадет не больше трёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, большее 3, либо событие Б — выпало число не больше 3. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что оба раза выпало число, большее 3 равна
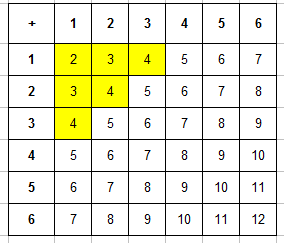
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 4 или 7.
Сумма двух выпавших чисел будет равна 4 в трех случаях(1 и 3, 3 и 1, 2 и 2) и 7 в шести случаях(1 и 6, 6 и 1, 2 и 5, 5 и 2, 3 и 4, 4 и 3), т. е. 9 благоприятных событий. А всего событий может быть 6 · 6 = 36, значит, вероятность равна
Игральную кость бросают дважды. Найдите вероятность того, что оба раза выпало число, меньшее 4.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет меньше четырёх очков» удовлетворяют три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет меньше четрёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, меньшее 4, либо событие Б — выпало число не меньше 4. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что хотя бы раз выпало число, меньшее 4 равна
Игральную кость бросают дважды. Найдите вероятность того, что наибольшее из двух выпавших чисел равно 5.
При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Число 5 будет наибольшим из выпавших, если хотя бы один раз выпадает 5 и ни разу — 6. То есть либо на первом кубике должно выпасть 5 очков, а на втором — любое число кроме 6, либо наоборот, на втором кубике должно выпасть 5, а на первом — любое число кроме 6. Также необходимо помнить, что при таком подсчёте вариант, когда на обоих кубиках выпадает пять, мы учитываем дважды: 5 + 5 − 1 = 9. Поэтому вероятность того, что наибольшее из двух выпавших чисел — 5
Игральную кость бросают дважды. Найдите вероятность того, что наименьшее из двух выпавших чисел равно 2.
При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Число 2 будет наименьшим из выпавших, если хотя бы один раз выпадает 2 и ни разу — 1. То есть либо на первом кубике должно выпасть 2 очка, а на втором — любое число кроме 1, либо наоборот, на втором кубике должно выпасть 2, а на первом — любое число кроме 1. Также необходимо помнить, что при таком подсчёте вариант, когда на обоих кубиках выпадает двойка, мы учитываем дважды: 5 + 5 − 1 = 9. Поэтому вероятность того, что наименьшее из двух выпавших чисел — 2
Игральный кубик бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел четна.
При бросании кубика два раза равновозможны 6 · 6 = 36 различных исходов. Сумма чётна, если на первом кубике выпадает нечётное число и на втором выпадает нечётное число, этому соответствует 3 · 3 = 9 исходов. Либо, если на обоих кубиках выпадают чётные числа, этому соответствует 3 · 3 = 9 исходов. Поэтому вероятность того, что сумма двух выпавших чисел чётна равна
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел нечетна.
При бросании кубика дважды равновозможны 6 · 6 = 36 различных исходов. Сумма нечётна, если на первом кубике выпадает нечётное число, а на втором выпадает чётное число, этому соответствует 3 · 3 = 9 исходов. Либо, если наоборот, на первом кубике выпадает чётное число, а на втором выпадает нечётное число, этому соответствует 3 · 3 = 9 исходов. Поэтому вероятность того, что сумма двух выпавших чисел нечётна равна
Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, меньшее 4.
При бросании кубика равновозможны шесть различных исходов. Событию «выпадет меньше четырёх очков» удовлетворяет три случая: когда на кубике выпадает 1, 2, или 3 очка. Поэтому вероятность того, что на кубике выпадет меньше четырёх очков равна Таким образом, при одном бросании кубика с одинаковой вероятностью реализуется либо событие А — выпало число, меньшее 4, либо событие Б — выпало число не меньше 4. То есть равновероятно четыре события: А-А, А-Б, Б-А, Б-Б. Поэтому вероятность того, что хотя бы раз выпало число, меньшее 4 равна
Приведем другое решение.
Вероятность того, что на кубике выпадет меньше четырех очков, равно 0,5. Найдем вероятность противоположного события, состоящего в том, что на кубике выпадет не меньше четырех очков: 1 − 0,5 = 0,5.
Вероятность того, что на обоих кубиках выпадут числа, не меньшие четырех, равна 0,5 · 0,5 = 0,25.
Событие «на обоих кубиках выпадут числа, не меньшие четырех очков» является противоположным событию «хотя бы один раз выпадет число, меньшее 4». Следовательно, вероятность того, что хотя бы один раз выпадет число, меньшее 4, равна 1 − 0,25 = 0,75
Решение задач о бросании игральных костей
Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.
Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).
Одна игральная кость
Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?
Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.
Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.
Две игральные кости
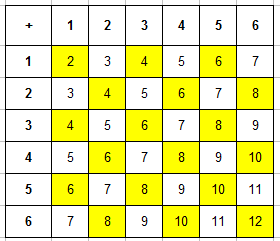
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.
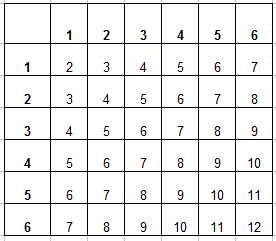
Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:
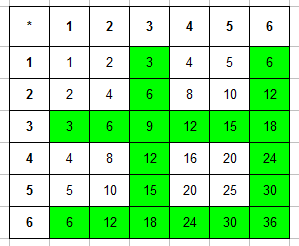
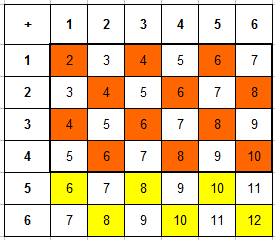
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:
Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).
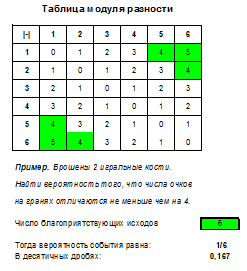
Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.
Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).
Другие задачи про кости и кубики
Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.
Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.
В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.
Теперь подберем такие исходы, которые дают в сумме 15 очков.
Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.
Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.
В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.
Приведем еще пример, решаемый аналогичным образом.
Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.
Полезные ссылки
Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.
В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.
Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.
Еще по теории вероятностей:
В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):
Новые задачи по теории вероятностей из Открытого Банка заданий ЕГЭ, 2021-2022 год
На этой странице – решения новых задач из Открытого Банка заданий, из которого формируется Банк заданий ФИПИ. Вы знаете, что в Проекте ЕГЭ-2022 в варианте Профильного ЕГЭ по математике не одна задача на теорию вероятностей, а две, причем вторая – повышенной сложности. Покажем, какие задачи могут вам встретиться на ЕГЭ-2022. Проект пока не утвержден, возможны изменения, но ясно одно – теория вероятностей на ЕГЭ будет на более серьезном уровне, чем раньше. Раздел будет дополняться, так что заходите на наш сайт почаще!
1. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Выпишем возможные варианты получения 8 очков в сумме:
| 2 | 6 |
| 6 | 2 |
| 3 | 5 |
| 5 | 3 |
| 4 | 4 |
Подходит только вариант 5; 3. Вероятность этого события равна 1 : 5 = 0,2 (один случай из 5 возможных).
2. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Благоприятными будут следующие исходы:
Первый раз – вытащили красный фломастер,
И второй раз – красный,
А третий раз – синий.
Вероятность вытащить красный фломастер (которых в ящике 4) равна
После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна
Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна
Вероятность события <красный – красный – синий >равна произведению этих вероятностей, то есть
3. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна Вероятность того, что первым вытащили красный, а вторым синий, равна
А если первым вытащили синий фломастер? Вероятность этого события равна Вероятность после этого вытащить красный равна вероятность того, что синий и красный вытащили один за другим, равна
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0,3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0,5 секунды… или одновременно!
Ответ: 0,3.
4. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Мы составили уравнение, решив которое, найдем вероятность
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна (пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна (у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Получим: отсюда z = 0,43.
Ответ: 0,43
Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.
5. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0,4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0,4.
С вероятностью 0,6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна
6. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.
Формула Бернулли:
– Вероятность того, что в независимых испытаниях некоторое случайное событие наступит ровно раз, равна:
– вероятность появления события в каждом испытании;
– вероятность непоявления события в каждом испытании.
Коэффициент часто называют биномиальным коэффициентом.
О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.
А пока скажем просто, как их вычислять.
Нет, это не заклинание. Не нужно громко кричать: Эн. Поделить на эм! И на эн минус эм! 🙂 То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы.
На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,
Пусть вероятность выпадения орла при одном броске монеты равна вероятность решки тоже Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.
Вероятность выпадения ровно 4 орлов равна
Найдем, во сколько раз больше, чем
7. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?
Стрелок поражает мишень с первого или со второго выстрела;
Вероятность поразить мишень равна
Вероятность поразить 5 мишеней из 5 равна
Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:
8. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Ресторан «Шеш-Беш» должен сказать составителям задачи спасибо: теперь популярность вырастет во много раз 🙂
Заметим, что условие не вполне корректно. Например, я бросаю кости и при первом броске получаю 5 и 6 очков. Надо ли мне бросать второй раз? Могу ли я получить 2 десерта, если дважды выброшу комбинацию из 5 и 6 очков?
Поэтому уточним условие. Если при первом броске получилась комбинация из 5 и 6 очков, то больше кости я не бросаю и забираю свой десерт (или кофе).
Если первый раз не получилось – у меня есть вторая попытка.
Решим задачу с учетом этих условий.
При броске одной игральной кости возможны 6 исходов, при броске 2 костей 36 исходов. Только два из них благоприятны: это 5; 6 и 6; 5, вероятность каждого из них равна Вероятность выбросить 5 и 6 при первом броске равна
Вероятность того, что с первой попытки не получилось, равна
Если в первый раз не получилось выбросить 5 и 6, а во второй раз получилось – вероятность этого события равна
Вероятность выбросить 5 и 6 с первой или со второй попытки равна (приблизительно равно, символом) 0,11.
9. Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что был сделан один бросок? Ответ округлите до сотых.
Рассмотрим возможные варианты. Игральную кость могли бросить:
1 раз, выпало 4 очка. Вероятность этого события равна (1 благоприятный исход из 6 возможных). При этом, если получили 4 очка, кость больше не бросаем.
2 раза, выпало 3 и 1 или 1 и 3 или 2 и 2. При этом, если получили 4 очка, больше не бросаем кость. Для 2 бросков: всего 36 возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна
3 раза, выпало 1, 1, 2 или 1, 2, 1 или 2, 1, 1. Если получили 4 очка – больше не бросаем кость. Для 3 бросков: всего возможны исходов, из них 3 благоприятных, вероятность получить 4 очка равна
4 раза, каждый раз по 1 очку. Вероятность этого события равна
Вероятность получить 4 очка равна
Воспользуемся формулой условной вероятности.
Пусть — вероятность получить 4 очка, сделав 1 бросок; (для одного броска: 6 возможных исходов, 1 благоприятный);
— вероятность получить 4 очка с одной или нескольких попыток,
— вероятность, что при этом был сделан только один бросок;
10. В викторине участвуют 6 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды.
Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых трех играх победила команда А. Какова вероятность того, что эта команда выиграет следующий раунд?
Пусть силы команд равны 1, 2, 3, 4, 5 и 6.
В трех раундах участвуют 4 команды, то есть выбирается 4 числа из 6 и среди этих четырех находится наибольшее.
Выпишем в порядке возрастания, какие 4 команды могли участвовать в первых трех раундах:
И наконец, хитроумная задача, совсем не похожая на школьную теорию вероятностей. В математике ее называют «задачей о разорении игрока». Это уже крутейший теорвер! Будем надеяться, что в варианты ЕГЭ ее все-таки включать не будут.
11. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 0,8 на единицу больше предыдущего и с вероятностью 1 – р меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен – 1?
Поскольку из точки 0 можно пойти вверх или вниз, и эти события несовместны, получим:
По условию, Тогда
Корни этого уравнения: или
А теперь представим себе, что будет, если эту задачи все-таки включат в курс подготовки к ЕГЭ. Учителя будут говорить ученикам: если тебе надо попасть из 0 в точку – 1, вероятность перехода вверх равна р, вероятность перехода вниз равна q, и если то в ответе будет а если то в ответе будет 1. Бессмысленная зубрежка, короче говоря.
Задачи, разобранные в этой статье, взяты из Открытого Банка заданий ЕГЭ по математике: mathege.ru
«Открытость и прозрачность ЕГЭ, наличие открытых банков, дает возможность развивать различные ресурсы, способствующие повышению качества образования.
При этом вся официальная информация, спецификации, демонстрационные варианты, открытые банки, содержатся только на сайте ФИПИ. Типы заданий, которые будут включены в ЕГЭ по математике в 2022 году прошли широкое обсуждение и апробацию в регионах, соответствуют ФГОС.
ФИПИ не комментирует содержание других ресурсов».
Ждем, когда на сайте ФИПИ появятся подборки задач №10 ЕГЭ-2022.
Новые задачи по теории вероятностей
Рассмотрим решение новых задач по теории вероятностей, которые появятся в ЕГЭ по математике в 2022 году.
Вы можете попробовать решить задачи самостоятельно, а потом сверить свое решение с предложенным.
1. № 508755
Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что в первый раз выпало 6 очков.
Нам нужно найти вероятность того, что в первый раз выпало 6 очков при условии, что вы сумме выпало 8 очков.
Воспользуемся формулой Байеса.
Пусть событие А «в сумме выпало 8 очков»
Событие В «в первый раз выпало 6 очков И в сумме выпало 8 очков»
Искомая вероятность равна
Если всего в сумме выпало 8 очков, то возможны такие варианты бросков:
Вероятность этого события
В первый раз выпало 6 очков И в сумме выпало 8 очков всего в одном случае, и вероятность этого события равна
Тогда вероятность равна
2. № 508769
Игральную кость бросили два раза. Известно, что три очка не выпали ни разу. Найдите при этом условии вероятность события «сумма выпавших очков окажется равна 8».
Представим число 8 в виде суммы двух слагаемых, каждое из которых принимает значения от 1 до 6 (возможное число очков):
По условию задачи сумма (2) нам не подходит.
Сумма (1) выпадает в двух случаях: 2+6 и 6+2.
Сумма (3) выпадает в одном случае.
При бросании кости 2 раза получаем 
3. № 508781
Симметричную монету бросают 11 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
При каждом броске монеты получаем 2 возможных исхода: орел или решка. При броске монеты 11 раз имеем 
Найдем число благоприятных исходов для события А. Оно равно числу способов выбрать из 11 элементов 5. То есть мы ищем число сочетаний из 11 по 5.
Сократим дробь и получим:
Таким образом, 
Найдем число благоприятных исходов для события B. Оно равно числу способов выбрать из 11 элементов 4. То есть мы ищем число сочетаний из 11 по 4.
Сократим дробь и получим:
Таким образом, 
Найдем 
4. № 508791
В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно две игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Вероятность получить определенную комбинацию очков при одновременном бросании костей такая же, как при их последовательном бросании.
При бросании двух костей имеем 
Найдем число благоприятных исходов в каждой попытке: нас устраивает: если гость выбросит (5 и 6) очков или (6 и 5) очков, то есть 2 благоприятных исхода.
Следовательно, вероятность получить искомую комбинацию в первой попытке равна
Вторая попытка необходима, если первая неудачна. Вероятность того, что первая попытка неудачна, равна
Вторая попытка, то есть одновременное бросание двух костей второй раз ничем не отличается от первой.
Итак, считаем вероятность того, что «искомая комбинация выпала при первой попытке» ИЛИ «искомая комбинация НЕ выпала при первой попытке И выпала при второй попытке».
Вероятность получить искомую комбинацию в первой ИЛИ второй попытке равна сумме вероятностей:
5. № 508793
Игральную кость бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 4. Какова вероятность того, что потребовалось сделать три броска? Результат округлите до сотых.
Заметим, что уже известно, что сумма всех выпавших очков равна 4. Это ограничивает число возможных вариантов бросков.
Рассмотрим все возможные варианты. Для этого представим число 4 в виде различных сумм слагаемых:
Найдем вероятность каждого исхода:
Вероятность того, что в сумме выпадет 4 очка, равна сумме вероятностей всех исходов:
Вероятность того, что в результате трех бросков сумма выпавших очков оказалась равна 4:
Нам нужно найти вероятность того, что сделано 3 броска при условии, что сумма всех выпавших очков равна 4.
Тогда по формуле Байеса
6. № 508798
Игральную кость бросали до тех пор, пока сумма выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось 3 броска? Ответ округлите до сотых.
Можно переформулировать вопрос так: какова вероятность, что сумма выпавших очков станет больше либо равна 4 на третьем броске?
Это возможно в случаях когда в первых двух бросках выпало 1+1, или 1+2, или 2+1. При этом в первом случае на третьем броске должно выпасть не меньше 2. А во втором и третьем случае на третьем броске может любое количество очков, сумма все равно будет больше либо равна 4. Тогда получаем, что вероятность равна
7. № 508809
Телефон передает SMS-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой отдельной попытке, равна 0,2. Найдите вероятность того, что для передачи сообщения потребуется не больше двух попыток.
Если вероятность того, что сообщение удастся передать без ошибок, равна 0,2, следовательно, вероятность того, что сообщение будет передано с ошибкой, равна 
Нарисуем дерево вероятностей.
Вероятность того, что сообщение будет верно передано в результате первой попытки, равна 0,2. Вероятность того, что сообщение будет верно передано в результате второй попытки, равна 

8. № 508820
При подозрении на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 91% случаев. Если заболевание нет, то тест выявляет отсутствие заболевания в среднем в 93% случаев. Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание? Результат округлите до сотых.
Нам нужно найти вероятность того, что пациент болен при условии, что известно, что у него ПЦР тест положительный. Пусть вероятность того, что пациент болен 

Нарисуем дерево вероятностей.
По условию в среднем тест оказывается положительным у 10% пациентов, к исходу «положительный тест» ведут красные линии.
Вероятность того, что пациент имеет положительный тест равна 0,1.
Получаем: если пациент здоров, то вероятность получить положительный тест равна 

Заметим, что вероятность того, что пациент болен И имеет положительный тест равна 
Теперь воспользуемся формулой Байеса. Нам нужно найти отношение вероятности того, что пациент болен И имеет положительный тест к вероятности того, что пациент имеет положительный тест.
9. № 508831
Стрелок в тире стреляет по мишени до тех пор, пока не поразит ее. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Сколько патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,5?
Если стрелок попадает в цель с вероятностью 0,2, то с вероятностью 0,8 он промахивается. Если стрелок промахивается, то он делает следующий выстрел.
Нарисуем дерево вероятностей:
Вероятность попасть в цель в результате одного выстрела равна 0,2.
Вероятность попасть в цель в результате двух выстрелов равна 
Вероятность попасть в цель в результате трех выстрелов равна 
Вероятность попасть в цель в результате четырех выстрелов равна 
10. № 508843
В ящике три красных и три синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что в первый раз синий фломастер появится третьим по счету?
Всего в ящике 6 фломастеров. Первый раз синий фломастер появится третьим по счету, если сначала будут вытащены 2 красных фломастера.
Вероятность первый раз вынуть красный фломастер равна
После этого в ящике останется 2 красных и 3 синих фломастера, всего 5 штук.
Вероятность второй раз вынуть красный фломастер равна
После этого в ящике останется 1 красный и 4 синих фломастера, всего 4 штуки.
Теперь вероятность вынуть синий фломастер равна 
Тогда вероятность того, что в первый раз синий фломастер появится третьим по счету равна произведению вероятностей:
11. №508851
Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0,6. Во сколько раз вероятность события «стрелок поразит ровно три мишени» больше вероятность события «стрелок поразит ровно две мишени».
Найдем вероятность того, что стрелок поразит мишень первым или вторым выстрелом. Если он попадает в мишень с вероятностью 0,6, то с вероятностью 1-0,6=0,4 он промахивается.
Нарисуем дерево вероятностей:
Мы видим, что вероятность того, что стрелок поразит мишень первым или вторым выстрелом, равна 

Найдем вероятность события «стрелок поразит ровно три мишени». Пусть стрелок первые три мишени поразит, а в последние две промахнется. Вероятность этого события равна 

Тогда
Тогда
Найдем отношение 
12. № 508868
В викторине участвуют 10 команд. Все команды разной силы, и в каждой встрече выигрывает та команда, которая сильнее. В первом раунде встречаются две случайно выбранные команды. Ничья невозможна. Проигравшая команда выбывает из викторины, а победившая команда играет со следующим случайно выбранным соперником. Известно, что в первых шести играх победила команда А. Какова вероятность, что эта команда выиграет седьмой раунд.
Команда А победила в шести играх, следовательно, она сыграла 6 матчей с шестью командами и оказалась самой сильной из них. В этих матчах приняло участие 7 команд.
Рассмотрим команды, которые уже сыграли. Присвоим каждой команде номер в зависимости от ее силы. Самая сильная команда имеет больший номер. Пусть, например, в нашем случае у команды А будет номер номер 7, а у проигравших команд будут номера от 1 до 6. Вероятность того, что команда А выиграет у всех остальных команд равна вероятности того, из 7 различных чисел у команды А номер 7. Эта вероятность равна 
Теперь нам нужно найти вероятность того, что команда А выиграет седьмой раунд. В седьмом раунде добавится еще одна команда. То есть мы будем иметь уже 8 команд, участвующих в викторине. Теперь у нас уже есть как бы набор из восьми различных чисел, характеризующих силу каждой команды. Найдем вероятность противоположного события: «команда А проиграет седьмой раунд». Это значит, что восьмая команда окажется сильнее, чем команда А. Это произойдет в том случае если из 8 различных неравных чисел у числа, характеризующего силу восьмой команды будет самое большое значение. Вероятность этого события равна 
Отсюда вероятность того, что команда А выиграет седьмой раунд равна
В общем случае получаем, что если команда выиграла в 


13. № 508871
Если в турнире участвуют 8 игроков, то в первом туре будет сыграно 4 партии, во втором 2 и в третьем 1 партия.
Иван и Алексей могут сыграть в первом туре. В первом туре соперником Ивана может быть один из семи игроков, то есть вероятность того, что это Алексей, равна 
Значит, вероятность того, что Иван и Алексей сыграли в первом туре равна 
Если Иван и Алексей не сыграли в первом туре, то они могут сыграть во втором. Для начала они должны выйти во второй тур. Для этого должны быть выполнены два условия: 1) они не сыграли друг с другом в первом туре (вероятность этого события 
Вероятность того, что они выйдут во второй тур равна 
Во второй тур выходят 4 человека, значит, при условии, что Иван и Алексей вышли во второй тур, вероятность сыграть друг с другом равна 
Таким образом, вероятность того, что Иван и Алексей вышли во второй тур И сыграли друг с другом равна 
Вероятность не сыграть друг с другом, при условии, что они вышли во второй тур равна 
Тогда они могут выйти в третий тур. Чтобы они вышли в третий тур необходимо выполнение двух условий: 1) они не сыграли друг с другом в первом туре И выиграли обе партии в первом туре, 2) они не сыграли друг с другом во втором туре И они победили каждый в своей партии во втором туре. Вероятность того, что это произойдет равна
Если они вышли в третий тур, то они точно сыграют друг с другом.
Таким образом, вероятность того, что Иван и Алексей сыграют друг с другом ИЛИ в первом туре, ИЛИ во втором ИЛИ в третьем туре, равна
Графически решение можно изобразить так:
14. № 508887
Первый игральный кубик обычный, а на гранях второго кубика нет четных чисел, а нечетные числа встречаются по два раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпали 3 и 5 очков. Какова вероятность, что бросали второй кубик?
При бросании первого кубика вероятность, что выпадут 3 и 5 очков, ИЛИ 5 и 3 очка равна 
Во втором кубике по две грани с числами 3 и 5, соответственно вероятность, что выпадут 3 и 5 очков, ИЛИ 5 и 3 очка равна 
Получили, что вероятность выпадения указанной комбинации при бросании второго кубика в 4 раза больше, чем при бросании первого. То есть из 5 серии бросков, при которых выпали числа 3 и 5, в среднем в 4-х случаях из пяти это будут броски второго кубика. Следовательно, вероятность того, что бросали второй кубик равна 0,8.
15. № 509078
Маша коллекционирует принцесс из Киндер-сюрпризов. Всего в коллекции 10 разных принцесс, и они равномерно распределены, то есть в каждом Киндер-сюрпризе может с равными вероятностями оказаться любая из 10 принцесс. У Маши есть две разные принцессы из коллекции. Какова вероятность того, что для получения следующей принцессы Маше придется купить еще 2 или 3 шоколадных яйца?
По условию покупка одного яйца не принесет Маше принцессу нового вида, то есть вероятность того, что Маша получит такую же принцессу, как у нее уже есть, равна 

Маша получит принцессу, отличную от тех, что у нее есть при покупке второго Киндер-сюрприза, если в первом купленном яйце будет такая же принцесса, как у нее есть, а во втором отличная от уже имеющихся. Вероятность этого события равна
Маша получит принцессу, отличную от тех, что у нее есть при покупке третьего Киндер-сюрприза, если в первом и втором купленном яйце будет такая же принцесса, как у нее есть, а в третьем отличная от уже имеющихся. Вероятность этого события равна
Тогда вероятность получить новую принцессу при покупке второго ИЛИ третьего Киндер-сюрприза равна
15. № 508885
Искомая вероятность находится по следующей формуле:
где