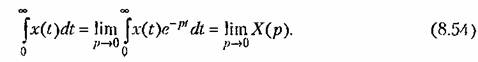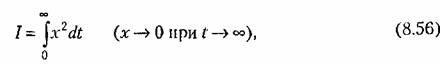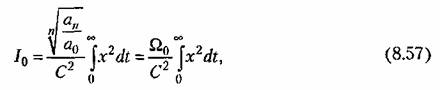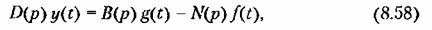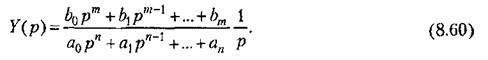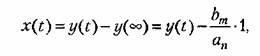Интегральная оценка это что
Большая Энциклопедия Нефти и Газа
Интегральная оценка
Интегральные оценки широко применяются при исследовании систем автоматического управления. Они позволяют оценить быстроту затухания и величину отклонения переменной регулирования совместно, без определения быстродействия и перерегулирования в отдельности. [1]
Интегральная оценка 1 может быть использована только для апериодических переходных процессов. Для колебательного переходного процесса, когда положительные полуволны чередуются с отрицательными, алгебраическая сумма площадей этих полуволн, определяемая интегралом Л, не может характеризовать качество переходного процесса. [2]
Интегральные оценки позволяют обобщенно оценить быстродействие технической системы и отклонение ее фазовых координат от установившихся значений в переходных процессах. [3]
Интегральные оценки (6.184) требуют большой вычислительной работы, и поэтому использование их ограничено. [4]
Интегральные оценки представляют собой определенные интегралы ( в процессах от 0 до) от функции времени х (), характеризующей течение переходного процесса в системе. [5]
Интегральная оценка / ] 0 применима только к системам, у которых переходные процессы монотонны, что резко ограничивает применимость данного критерия. Если переходной процесс колебательный ( рис. 7.12, б, кривая 1), то значение / 10 не может служить мерой его качества, так как площади разного знака под кривой переходного процесса будут вычитаться друг из друга. [7]
Интегральные оценки в качестве критерия оптимальности широко используются при синтезе оптимальных САУ. [8]
Интегральная оценка всей системы в целом дается по результатам функционального анализа деятельности оператора в системе управления. [9]
Интегральная оценка в баллах рассчитывается на базе использования методов научной экспертизы, цель которой заключается в установлении относительной значимости групп показателей для оценки деятельности НИИ и КБ, а также значимости отдельных показателей внутри группы. [10]
Интегральные оценки позволяют положить в основу расчета систем желаемую кривую переходного процесса. Совпадение графиков переходных процессов с этими кривыми соответствует нулевым значениям интегралов. Но в линейных системах равенство / 3 О невозможно, поскольку из-за инерционности систем недостижимы бесконечно большие ускорения, необходимые для совершения скачка. Случай, когда / 3 0, может встретиться редко даже при достаточно больших значениях т, так как обычно значительная часть параметров системы задана и варьирование одним-двумя параметрами не может придать уравнению форму и коэффициенты, отвечающие точно форме и коэффициентам желаемой экспоненты. [11]
Интегральная оценка представляется в виде средневзвешенной суммы частных показателей весовых коэффициентов, которые рассчитываются по методу экспертных оценок. [12]
Интегральные оценки выражаются определенными интегралами функций координат и их производных по времени. [13]
Интегральные оценки
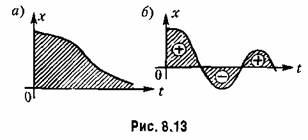
Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения управляемой величины в совокупности, без определения того и другого в отдельности. Простейшей интегральной оценкой может служить величина
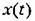
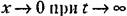
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.
Для вычисления интеграла (8.53) нет
необходимости в нахождении х(t), так как его можно легко вычислить, используя изображение Лапласа или Хевисайда-Карсона. Действительно, изображение Лапласа определяется выражением
Неудобством интегральной оценки вида (8.53) является то, что она годится только
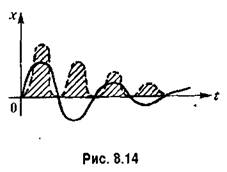
для монотонных процессов, когда не меняется знак отклонениях. Если же имеет место колебательный процесс (рис. 8.13, б), то при вычислении интеграла (8.53) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем управления может быть неизвестна, то применять интегральную оценку вида (8.53) оказывается практически нецелесообразным. Поэтому предлагалась другая интегральная оценка:
т. е. сумма абсолютных величин всех площадей под кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.
Квадратичная интегральная оценка. В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке
которая не зависит от знаков отклонений, а значит, и от формы переходного процесса (монотонной или колебательной).
Величина / (8.56) будет тем меньше, чем меньше сумма заштрихованных на рис. 8.14 площадей (взятых для квадратов ординат), т. е. чем лучше переходный процесс приближается к идеальному скачку управляемой величины вслед за скачком задающего или возмущающего воздействия. Ниже будет показано, что такая оценка не всегда является лучшей, но пока остановимся на ней.
Заметим, что оценку (8.56) называют также квадратичной динамической ошибкой. Ее можно записать в безразмерном виде:
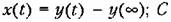
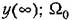
Рассмотрим один из возможных способов вычисления квадратичной интегральной оценки (8.56) при скачкообразном внешнем воздействии.
В общем случае дифференциальное уравнение системы (в символической операторной записи) согласно (5.5) имеет вид
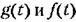
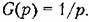
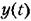
Отклонение х управляемой величины от нового установившегося состояния в переходном процессе, входящее в формулу (8.56), будет
Методика расчета интегральных оценок (рейтингов)
На первом шаге определялись интервалы допустимых значений показателей и их наилучшие значения. В зависимости от содержания показателя наилучшие значения могут быть максимальными, минимальными или другими оптимальными.
Затем проводилась нормировка значений показателей с помощью линейной функции принадлежности значений показателя стандартному интервалу [0; 1]. При нормировке показателей были сделаны следующие допущения:
1) если рост значения показателя рассматривается как положительная тенденция и фактическое значение показателя больше максимально допустимого, то нормированное значение показателя принимается равным 1 (если меньше минимально допустимого, то 0);
2) если рост значения показателя рассматривается как отрицательная тенденция и фактическое значение показателя больше максимально допустимого, то нормированное значение показателя принимается равным 0 (если меньше минимально допустимого, то 1).
При этих допущениях нормированное значение показателя определяется по формуле:
где x — фактическое значение показателя;
x1 — минимально допустимое значение показателя;
x2 — максимально допустимое значение показателя;
y — нормированное значение показателя.
После выполнения нормировки для каждого показателя определяется его значимость (вес). Сумма весов должна быть равна 1.
Интегральный показатель рейтинговой оценки рассчитывался по формуле:
где Ki — i-й показатель, участвующий в расчете рейтинга, а pi — его весовой коэффициент. Значения интегрального показателя находятся в пределах [0; 1]. После выполнения расчетов компании выстраивались в порядке возрастания значений интегрального показателя: чем меньше значение показателя, тем выше положение компании в рейтинге.
Геометрический смысл интегрального показателя рейтинговой оценки — это расстояние от точки с координатами из нормированных значений показателей сравниваемой компании до точки с единичными координатами, соответствующими эталонной компании. Таким образом, интегральный показатель определяет степень близости показателей сравниваемой компании к показателям эталонной компании.
После расчета интегрального показателя рейтинга выполнялась стратификация компаний по его значениям: все участвующие в рейтинге компании разбивались на соответствующее число групп (страт). Для этого интервал возможных значений интегрального показателя [0; 1] был разделен на это число равных интервалов.