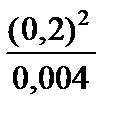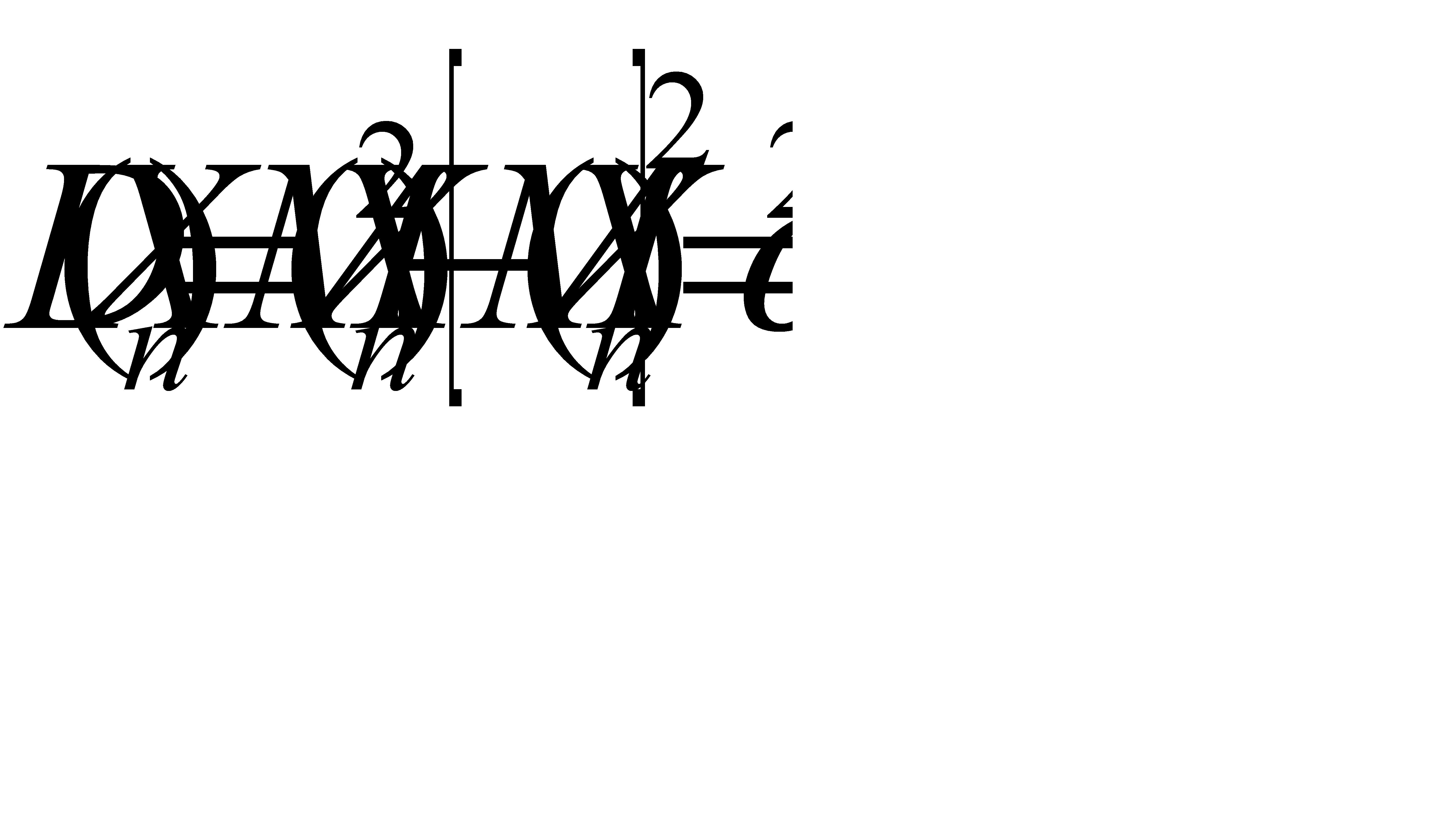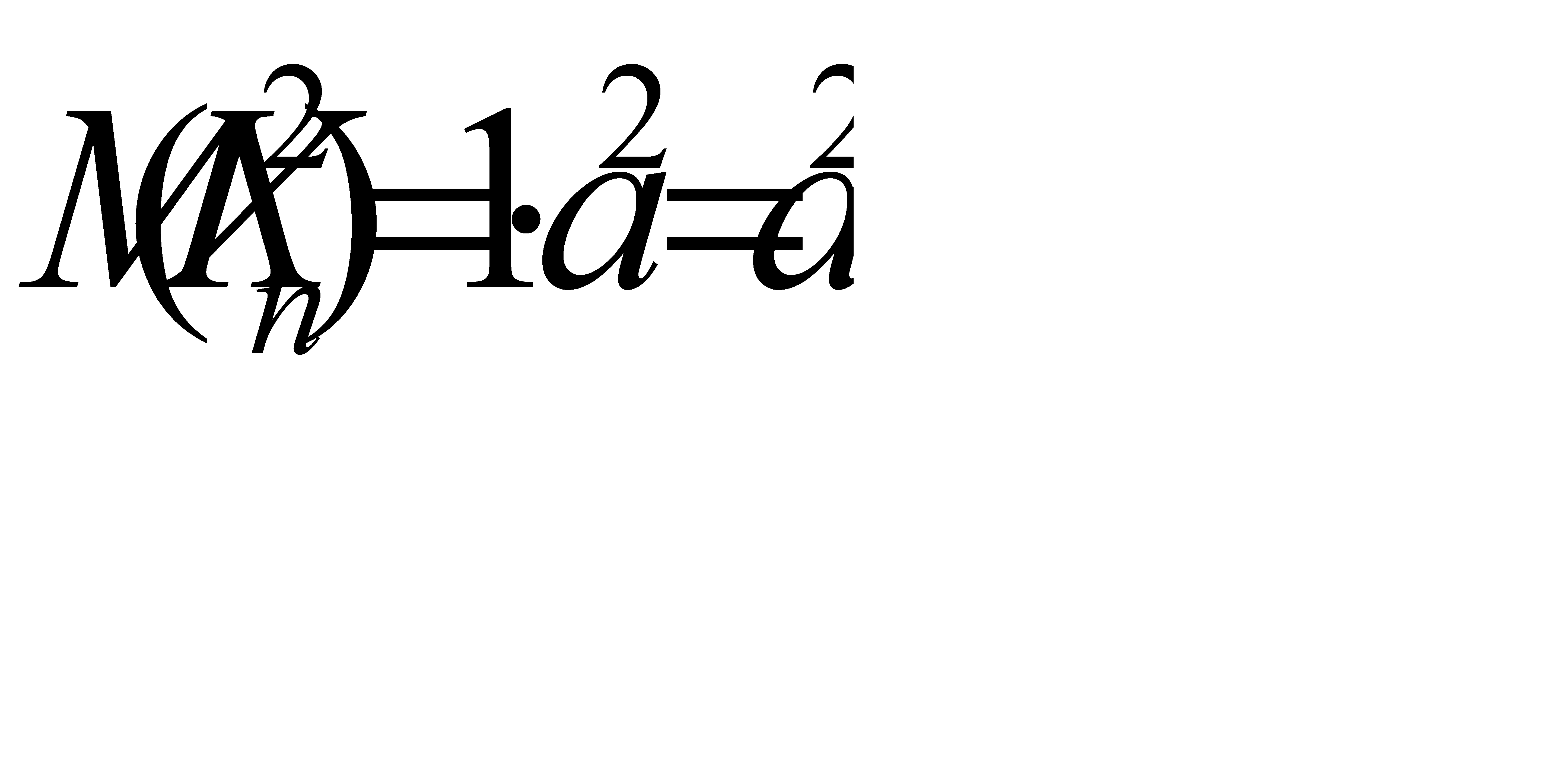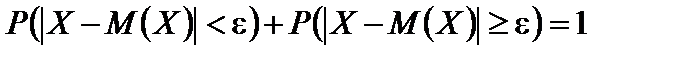Используя неравенство чебышева оценить вероятность того что
Используя неравенство чебышева оценить вероятность того что
7.1 оЕТБЧЕОУФЧБ нБТЛПЧБ Й юЕВЩЫЕЧБ
(тБУУНПФТЙН ФПМШЛП ДМС УМХЮБКОЩИ ЧЕМЙЮЙО ДЙУЛТЕФОПЗП ФЙРБ, РТЙОЙНБАЭЙИ ЛПОЕЮОПЕ ЮЙУМП ЪОБЮЕОЙК.)
ъБЖЙЛУЙТХЕН РТПЙЪЧПМШОЩН ПВТБЪПН ε > 0.
ч УЙМХ РТПЙЪЧПМШОПУФЙ ЧЩВПТБ ε ТЕЪХМШФБФ ВХДЕФ УРТБЧЕДМЙЧ ДМС МАВПЗП ε > 0.
ъбдбюб 7.1.1 пГЕОЙФШ ЧЕТПСФОПУФШ ПФЛМПОЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ПФ УЧПЕЗП УТЕДОЕЗП Mξ ОБ ЧЕМЙЮЙОХ, РТЕЧЩЫБАЭХА ХФТПЕООПЕ УТЕДОЕЛЧБДТБФЙЮЕУЛПЕ.
ъбдбюб 7.1.4 йЪЧЕУФЕО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ:
| xk | 0,1 | 0,4 | 0,6 |
| pk | 0,2 | 0,3 | 0,5 |
йУРПМШЪХС ОЕТБЧЕОУФЧП юЕВЩЫЕЧБ, ПГЕОЙФШ ЧЕТПСФОПУФШ 
.
Mξ = 0,1ћ0,2 + 0,4ћ0,3 + 0,6ћ0,5 = 0,44;
Mξ 2 = 0,01ћ0,2 + 0,16ћ0,3 + 0,36ћ0,5 = 0,23;
ъбдбюб 7.1.5 ч ПУЧЕФЙФЕМШОХА УЕФШ РБТБММЕМШОП ЧЛМАЮЕОП 20 МБНР. чЕТПСФОПУФШ ФПЗП, ЮФП ЪБ ЧТЕНС t МБНРБ ВХДЕФ ЧЛМАЮЕОБ, ТБЧОБ 0,8. пГЕОЙФШ ЧЕТПСФОПУФШ ФПЗП, ЮФП БВУПМАФОБС ЧЕМЙЮЙОБ ТБЪОПУФЙ НЕЦДХ ЮЙУМПН ЧЛМАЮЕООЩИ МБНР Й УТЕДОЙН ЮЙУМПН ЧЛМАЮЕООЩИ МБНР ЪБ ЧТЕНС t (НБФЕНБФЙЮЕУЛЙН ПЦЙДБОЙЕН) ПЛБЦЕФУС: Б) НЕОШЫЕ 3; В) ОЕ НЕОШЫЕ 3.
дБООБС УМХЮБКОБС ЧЕМЙЮЙОБ ξ РПДЮЙОСЕФУС ВЙОПНЙБМШОПНХ ЪБЛПОХ ТБУРТЕДЕМЕОЙС У РБТБНЕФТБНЙ (n,p); ЗДЕ n = 20, p = 0,8. (рПЮЕНХ?)
Dξ = npg = 20ћ0,8ћ0,2 = 3,2
уТБЧОЙН ДБООПЕ ЪОБЮЕОЙЕ УП ЪОБЮЕОЙЕН, РПМХЮБЕНЩН ОБ ПУОПЧБОЙЙ УМЕДУФЧЙК Л ЙОФЕЗТБМШОПК ФЕПТЕНЕ нХБЧТБ-мБРМБУБ (УНПФТЙ Р. 3.1.4).
ъОБЮЕОЙЕ ж(4,08) ОБИПДЙН РП ФБВМЙГЕ: ж(4,08) ≈ 0,99999 (УНПФТЙ рТЙМПЦЕОЙЕ).
ъБДБЮЙ ДМС УБНПУФПСФЕМШОПЗП ТЕЫЕОЙС.
ъбдбюб 7.1.1(у) пГЕОЙФШ ЧЕТПСФОПУФШ ФПЗП, ЮФП УМХЮБКОБС ЧЕМЙЮЙОБ ξ ПФЛМПОЙФУС ПФ УЧПЕЗП Mξ ОЕ НЕОШЫЕ, ЮЕН ОБ ДЧБ УТЕДОЕЛЧБДТБФЙЮЕУЛЙИ ПФЛМПОЕОЙС.
ъбдбюб 7.1.2(у) йЪЧЕУФЕО ЪБЛПО ТБУРТЕДЕМЕОЙС УМХЮБКОПК ЧЕМЙЮЙОЩ ξ:
| xk | 0,3 | 0,6 |
| pk | 0,2 | 0,8 |
ъбдбюб 7.1.3(у) хУФТПКУФЧП УПУФПЙФ ЙЪ 10 ОЕЪБЧЙУЙНП ТБВПФБАЭЙИ ЬМЕНЕОФПЧ. чЕТПСФОПУФШ ПФЛБЪБ ЛБЦДПЗП ЬМЕНЕОФБ ЪБ ЧТЕНС t ТБЧОБ 0,05.пГЕОЙФШ ЧЕТПСФОПУФШ ФПЗП, ЮФП БВУПМАФОБС ЧЕМЙЮЙОБ ТБЪОПУФЙ НЕЦДХ ЮЙУМПН ПФЛБЪБЧЫЙИ ЬМЕНЕОФПЧ Й УТЕДОЙН ЮЙУМПН ПФЛБЪПЧ ЪБ ЧТЕНС t (НБФЕНБФЙЮЕУЛЙН ПЦЙДБОЙЕН) ПЛБЦЕФУС: Б) НЕОШЫЕ ДЧХИ; В) ОЕ НЕОШЫЕ ДЧХИ.
ъбдбюб 7.1.4(у) чЕТПСФОПУФШ РПСЧМЕОЙС УПВЩФЙС б Ч ЛБЦДПН ЙУРЩФБОЙЙ ТБЧОБ 1/2. пГЕОЙФШ ЧЕТПСФОПУФШ ФПЗП, ЮФП ЮЙУМП РПСЧМЕОЙК УПВЩФЙС б ВХДЕФ ЪБЛМАЮЕОП Ч РТЕДЕМБИ ПФ 40 ДП 60, ЕУМЙ ВХДЕФ РТЙЪЧЕДЕОП 100 ОЕЪБЧЙУЙНЩИ ЙУРЩФБОЙК.
© гЕОФТ ДЙУФБОГЙПООПЗП ПВТБЪПЧБОЙС пзх, 2000-2002
Так как события и противоположные, то сумма их вероятностей равна единице. Т.е.,
№238 Используя неравенство Чебышева в форме, приведенной в задаче 237, оценить вероятность того, что случайная величина X отклонится от своего математического ожидания не меньше чем на два средних квадратических отклонения.
№239 Используя неравенство Чебышева, оценить вероятность того, что
№240 Дано : 
и 
Используя неравенство Чебышева, оценить ε снизу.
№241 Устройство состоит из 10 независимо-работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется:
Воспользуемся неравенством Чебышева:
Подставив сюда М (Х)=0,5; D(X) =0,475, e = 2, получим
P (| X- 0.5 | =1-(0.475/4)=0.88
б) События |X-0.5| =2 противопоположны, поэтому сумма их вероятностей равна единице. Следовательно,
Найдем максимальную разность между заданным числом появлений события и математическим ожиданием М(Х) = 200:
Воспользуемся неравенством Чебышева в форме
Проверим, выполняется ли требование конечности математических ожиданий:
Таким образом, каждая случайная величина имеет конечное (равное нулю) математическое ожидание, т.е. второе требование теоремы выполняется.
Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения 
:
 |  | | |
| p |  |  | |
или, сложив вероятности одинаковых возможных значений,
| | | |
| p |  | |
Найдём математическое ожидание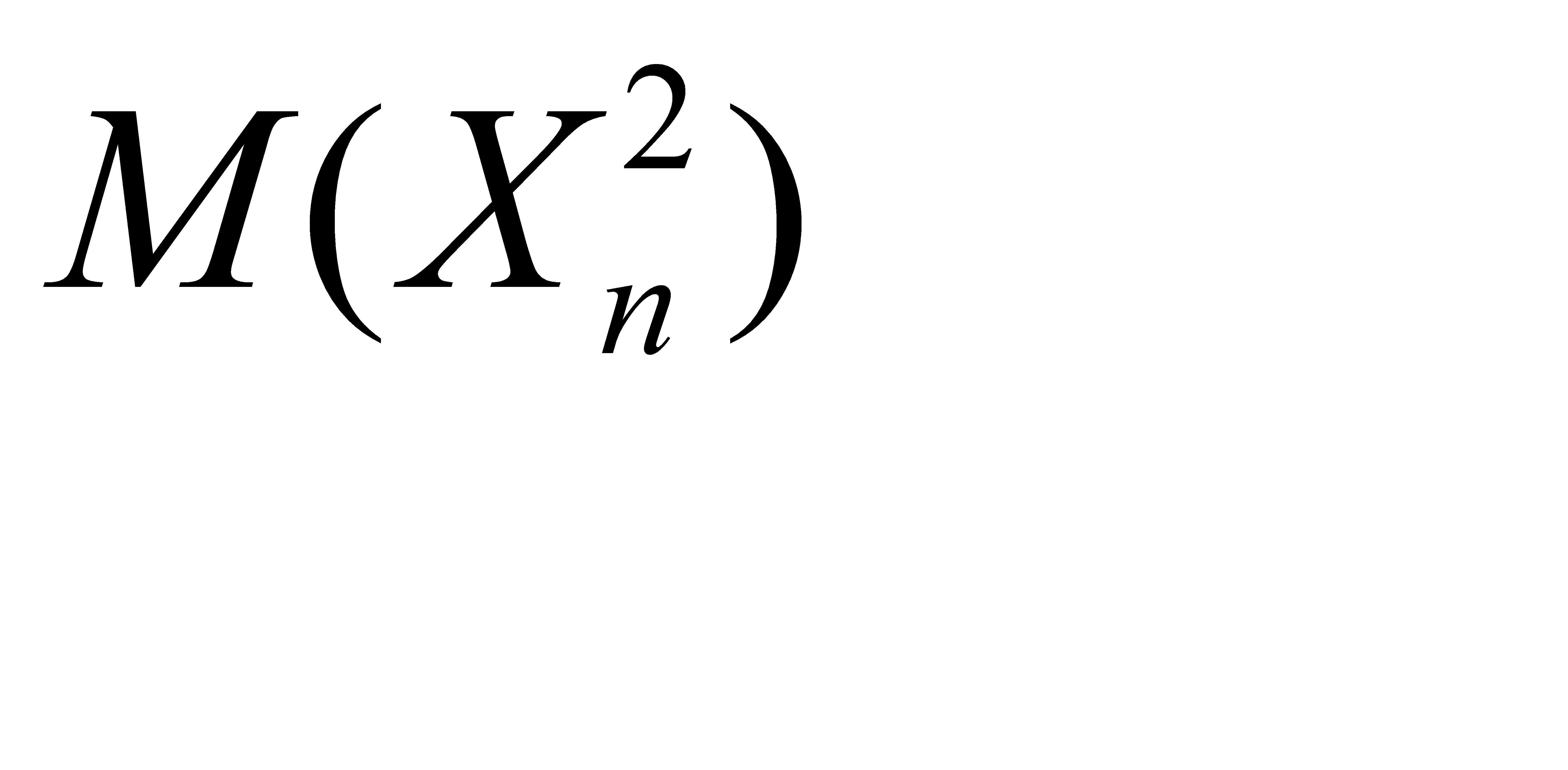 
:
Найдём дисперсию 
:
Таким образом, дисперсии заданных случайных величин равномерно ограничены
числом 
, т.е. третье требование выполняется.
Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
№248 Последовательность независимых случайных величин 
задана законом распределения
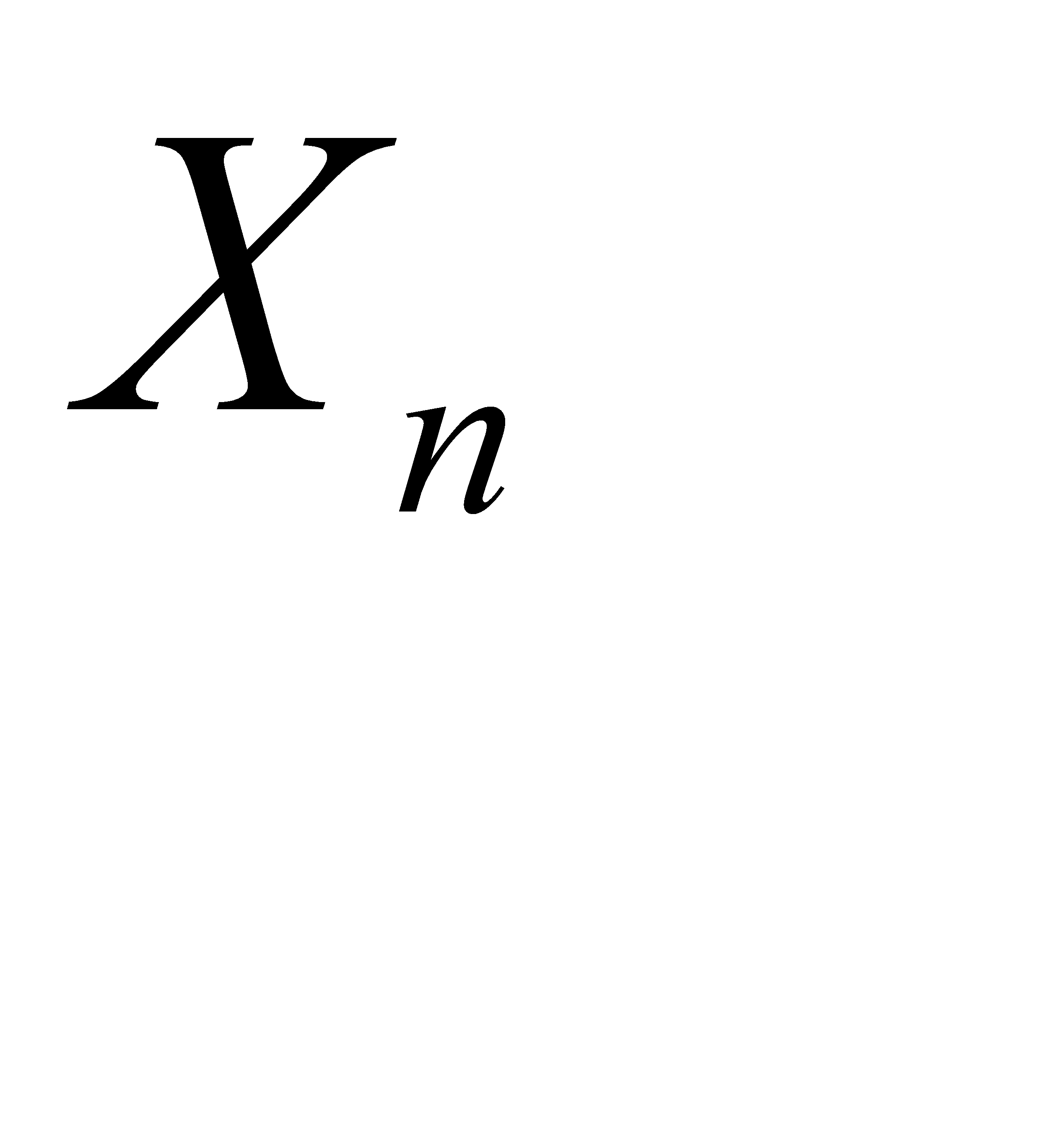 | a | -a |
| p |  |  |
Применима ли к заданной последовательности теорема Чебышева?
Для того, чтобы к последовательности случайных величин была применимы теорема Чебышева, достаточно, чтобы
1) эти величины были попарно независимы,
2) имели конечные математические ожидания,
3) имели равномерно ограниченные дисперсии.
Поскольку случайные величины независимы, то они подавно попарно независимы, т.е. первое требование теоремы Чебышева выполняется.
Проверим, выполняется ли требование конечности математических ожиданий:
Таким образом, каждая случайная величина имеет конечное (равное 
) математическое ожидание, т.е. второе требование теоремы выполняется.
Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения :
| | a 2 | a 2 |
| p | | |
или, сложив вероятности одинаковых возможных значений,
| | a 2 |
| p |
Найдём математическое ожидание :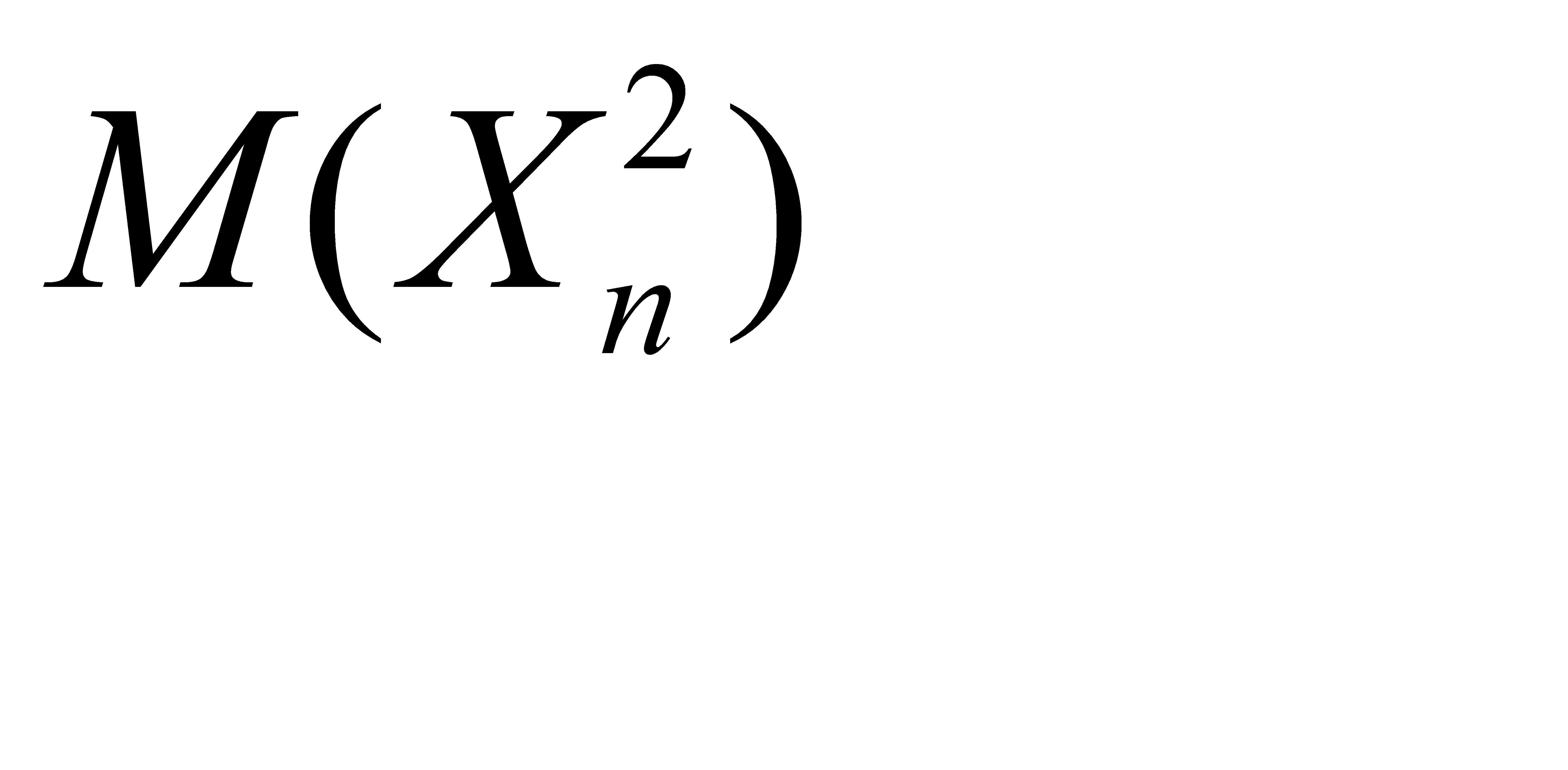
Найдём дисперсию :
Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:
Таким образом, дисперсии заданных случайных величин равномерно ограничены
числом 
, т.е. третье требование выполняется.
Итак, поскольку все требования выполняются, к рассматриваемой последовательности случайных величин теорема Чебышева применима.
Спесивцева Наталья
№249 Последовательность независимых случайных величин задана законом распределения
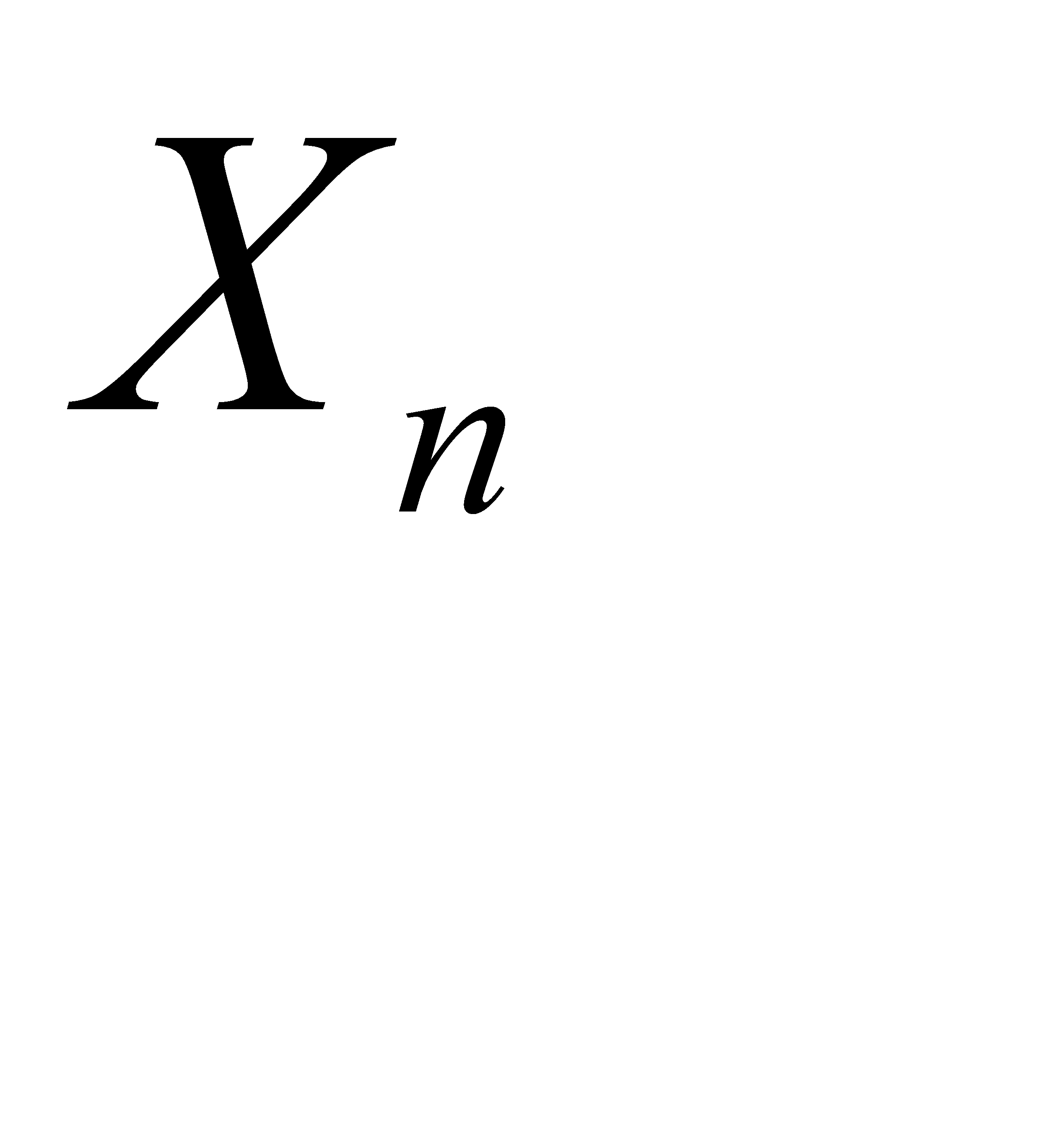| | n+1 | -n |
| p | | |
А) убедиться, что требование теоремы Чебышева о равномерной ограниченности дисперсии не выполняется
Б) можно ли отсюда заключить, что к рассматриваемой последовательности теорема Чебышева неприменима?
А) Найдём математическое ожидание 
:
Проверим, выполняется ли требование равномерной ограниченности дисперсии. Напишем закон распределения :
| |  |  |
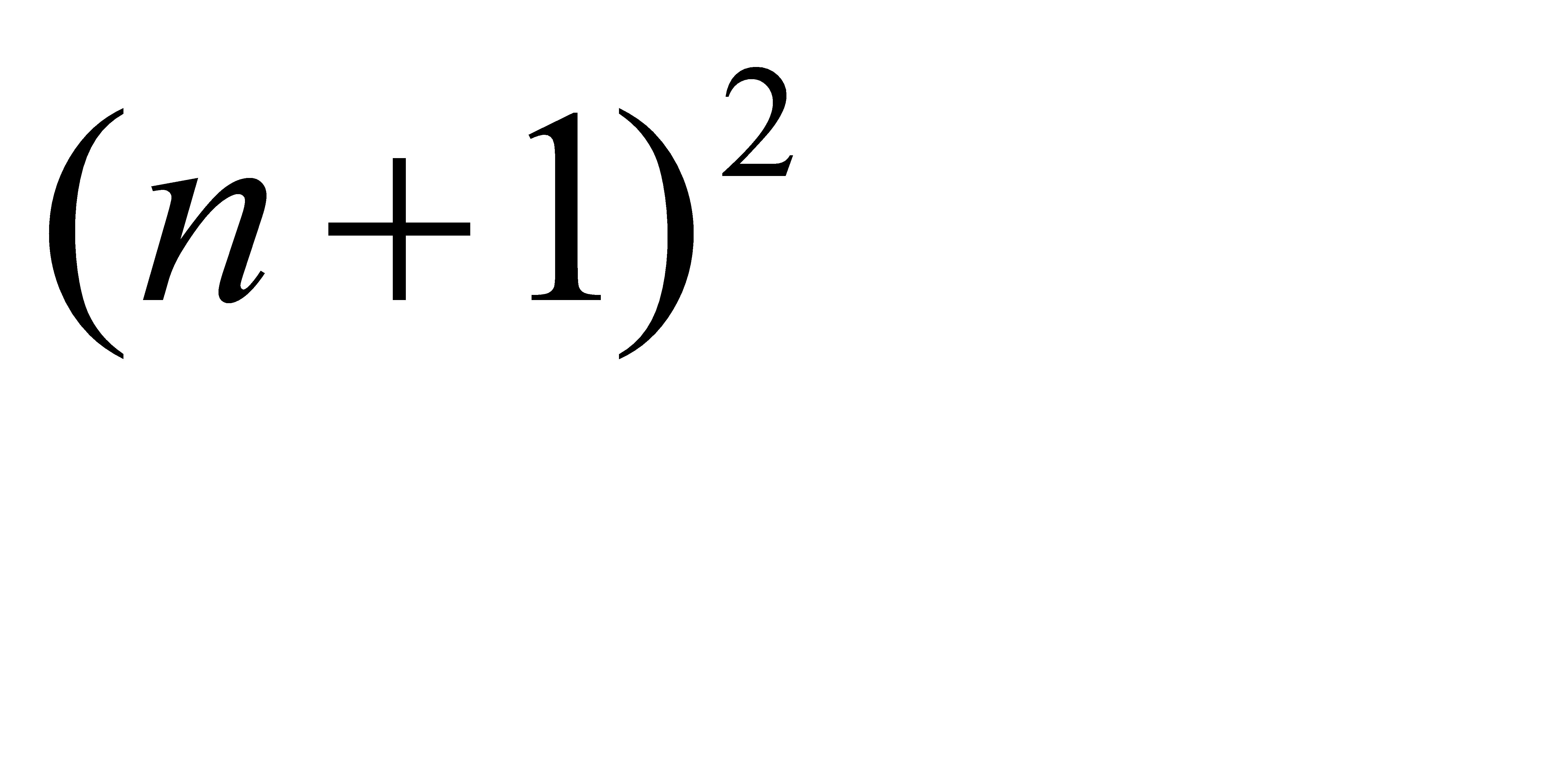| p | | |
Найдём математическое ожидание :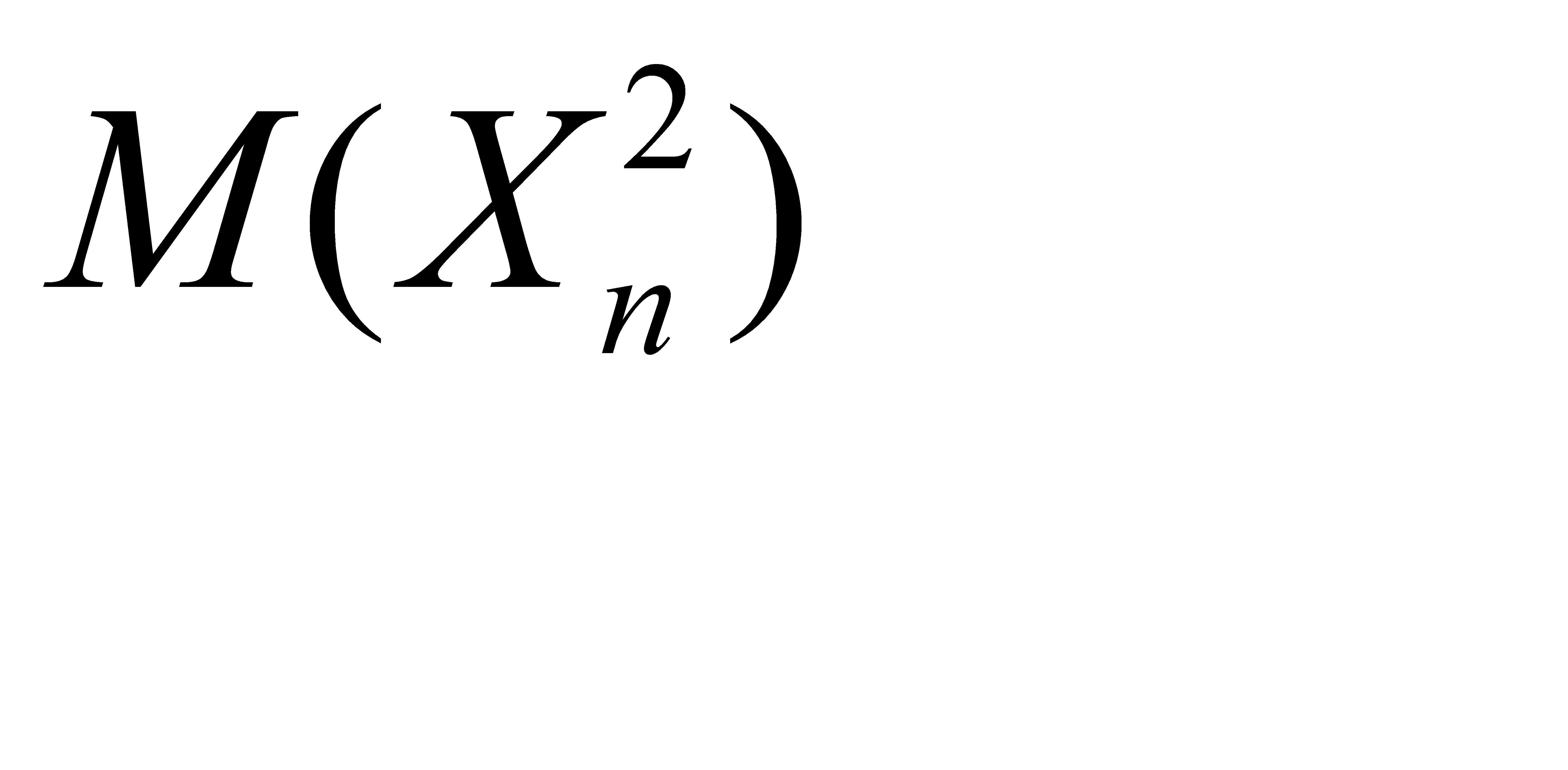
Найдём дисперсию :
Эта функция возрастает, следовательно, чтобы вычислить константу, ограничивающую дисперсию, можно вычислить предел:
Таким образом, дисперсии заданных случайных величин неограниченны, что и требовалось доказать.
Б) Из формулировки теоремы Чебышева следует, что требование равномерной ограниченности дисперсий является достаточным, но не необходимым условием, поэтому нельзя утверждать, что к данной последовательности эту теорему применить нельзя.
№250 Последовательность независимых случайных величин Х1, Х2, …, Хn, … задана законом распределения
Применима ли к заданной последовательности теорема Чебышева?
Поскольку случайные величины Хn независимы, то они подавно и попарно независимы, т.е. первое требование теоремы Чебышева выполняется.
Легко найти, что M(Xn)=0, т.е.первое требование конечности математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле
учитывай, что M(Xn)=0, найдем (выкладки предоставляются выполнить читателю)
Приравняв первую производную этой функции к нулю, найдем критические точки х1=0 и х2=ln 2.
Отбросим первую точку как не представляющую интереса (n не принимает значения, равного нулю); легко видеть, что в точек х2=2/ln 2 функция φ(х) имеет максимум. Учитывая, что 2/ln 2 ≈ 2.9 и что N – целое положительное число, вычислим дисперсию D(Xn)= (n 2 /2 n-1 )α 2 для ближайших к числу 2.9 (слева и справа) целых чисел, т.е. для n=2 и n=3.
Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.
№251 Последовательность независимых случайных величин X1, X2, …, Xn, … задана законом распределения
Применима ли к заданной последовательности теорема Чебышева?
Замечание. Поскольку случайные величины Х, одинаково распределены и независимы, то читатель, знакомый с теоремой Хинчина, может ограничиться вычислением лишь математического ожидания и убедиться, что оно кончено.
Поскольку случайные величины Хn независимы, то они подавно и попарно независимы, т.е. первое требование теоремы Чебышева выполняется.
Легко найти, что M(Xn)=0, т.е.первое требование конечности математических ожиданий выполняется.
Остается проверить выполнимость требования равномерной ограниченности дисперсий. По формуле
учитывай, что M(Xn)=0, найдем
Таким образом, наибольшая возможная дисперсия равна 2, т.е. дисперсии случайных величин Хn равномерно ограничены числом 2.
Итак, все требования теоремы Чебышева выполняются, следовательно, к рассматриваемой последовательности эта теорема применима.
№252 Случайная величина Х задана функцией распределения
Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0, 1/3).
По определению функции распределения,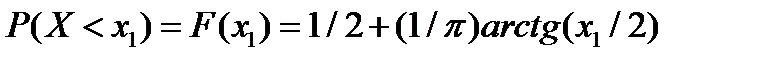 
.
Следовательно, ½+(1/π)arctg(x1/2)=(3/4), или 
. Отсюда x1/2=1, или x1=2.
№259 Случайная величина X задана на всей оси Ox функцией распределения 
. Найти возможное значения x1, удовлетворяющее условию: с вероятностью 1/6 случайная X в результате испытания примет значение большее x1.
По определению функции распределения, .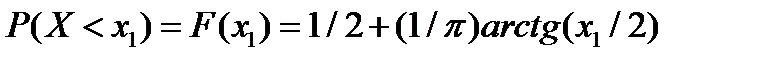
Следовательно, ½+(1/π)arctg(x1/2)=(3/4), или 
. Отсюда, 
или 
.
№260 Дискретная случайная величина X задана законом распределения
Найти функцию распределения F(x) и начертить ее график.
Решение.
Если x ≤ 2, то F(x)=0. Действительно, значений меньших 2 величина X не принимает. Следовательно, при x ≤ 2 функция F(x)=P(X
Неравенство Маркова. Неравенство Чебышева
На этой странице мы собрали примеры решения учебных задач по теории вероятностей, в которых применяются неравенство Маркова, неравенство Чебышева, теорема Чебышева и их следствия (закон больших чисел, ЗБЧ).
Краткая теория. Закон больших чисел
Неравенство Маркова дает вероятностную оценку того, что значение неотрицательной случайной величины превзойдет некоторую константу через известное математическое ожидание. Когда никаких других данных о распределении нет, неравенство дает некоторую информацию, хотя зачастую оценка груба или тривиальна.
Альтернативная форма записи (когда нужно оценить вероятность того, что СВ меньше некоторой константы):
Когда известны не только математическое ожидание (первый момент), но и дисперсия (второй центральный момент) для случайной величины (и они конечны), можно применять следствие неравенства Маркова — неравенство Чебышева, которое дает оценку вида:
Также его можно записать в другой форме:
Приведем также теорему Чебышева, которая имеет большое практические значение.
Примеры решенных задач
Неравенство Маркова: примеры решений
Задача 1. Среднее количество вызовов, поступающих на коммутатор завода в течение часа, равно 300. Оценить вероятность того, что в течение следующего часа число вызовов на коммутатор: а) превысит 400; б) будет не более 500.
Задача 2. Количество потребляемой за сутки электроэнергии предприятием является случайной величиной с математическим ожиданием 6 мегаватт при среднем квадратическом отклонении 1,5 мегаватта. Оценить вероятность того, что в ближайшие сутки потребление электроэнергии окажется более 12 мегаватт.
Неравенство Чебышева: примеры решений
Задача 4. В 1600 испытаниях Бернулли вероятность успеха в каждом испытании равна 0,3. С помощью неравенства Чебышева оценить вероятность того, что разница между числом успехов в этих испытаниях и средним числом успехов будет меньше 50.
Задача 6. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется меньше двух.
Теорема Чебышева и ЗБЧ: примеры решений
Задача 8. Вероятность того, что абсолютная величина отклонения средней арифметической случайных величин от средней арифметической их математических ожиданий не превышает 0,5, равна 0,8. Дисперсия каждой независимой случайной величины не превышает 7. Найти число таких случайных величин.
Задача 9. Дисперсия каждой из 2500 независимых СВ не превышает 5. Оценить вероятность того, что отклонение среднего арифметического этих случайных величин от среднего арифметического их математических ожиданий не превысит 0,4.
Решебник по терверу
Нужны еще решения? Найди в решебнике сейчас:
Неравенство Чебышева
Теорема. Каково бы ни было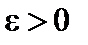 
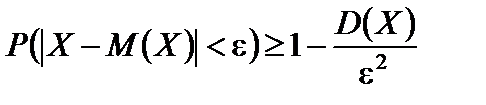
для любой случайной величины Х, дисперсия которой конечна, имеет место неравенство Чебышева
. (6.3)
Известно, что сумма вероятностей двух противоположных событий равна единице, следовательно,
.
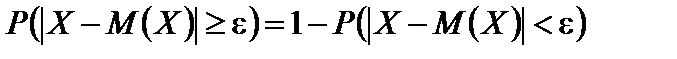
Отсюда и из неравенства (6.3) следует, что
. (6.4)
Неравенство (6.4) называют второй формой неравенства Чебышева.
Тест 6.5. чтобы для случайной величины Х имело место неравенство Чебышева, она должна обладать свойством:
1) математическое ожидание M(X) конечно;
2) дисперсия D(X) конечна;
Пример 6.3. Случайная величина X имеет дисперсию D(X) = 1,66. Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 2.
По условию D(X) = 1,66, e = 2. Применяя неравенство (6.3), находим 
.
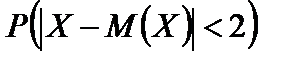
Ответ: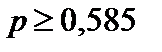 
.
Пример 6.4. Случайная величина X имеет дисперсию D(X) = 0,001.
Используя неравенство Чебышева, оценить вероятность того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,1.
По условию D(X) = 0,001, e = 0,1.
Применяя неравенство (6.4), находим
.
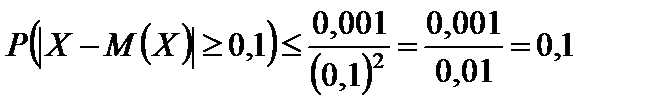
Ответ: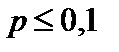 
.
Тест 6.6. Случайная величина X имеет дисперсию D(X) = 1620. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине менее чем на 200, по неравенству Чебышева является выражение:
1) 
;
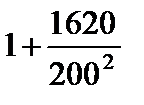
2) 
;
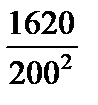
3) 
;
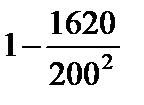
4) 
;
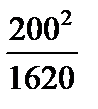
5) 
.
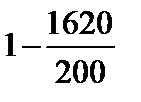
Тест 6.7. Случайная величина X имеет дисперсию D(X) = 0,004. Оценкой вероятности того, что случайная величина X отличается от своего математического ожидания по абсолютной величине не менее чем на 0,2, по неравенству Чебышева является выражение:
1) 
;
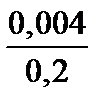
2) 
;
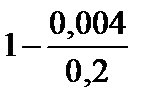
3) 
;
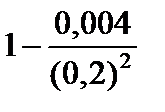
4) 
;
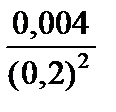
5) 
.