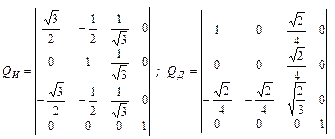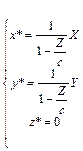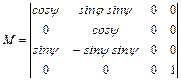Изометрия и диметрия чем отличаются

Аксонометрические проекции

Для того чтобы наиболее наглядно передать форму изделий и предметов, ясно и понятно представить схемы взаимодействия различных деталей, по мере надобности применяются аксонометрические проекции.

Прямоугольная изометрическая проекция

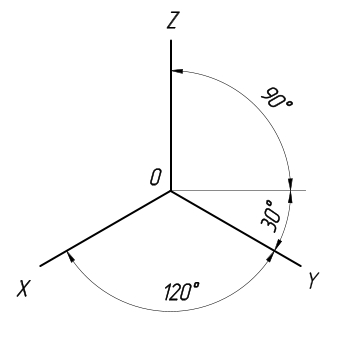
Проекция этого вида отличается тем, что в ней оси аксонометрии располагаются друг по отношению к другу под углом 120°. При этом искажения изображения по всем аксонометрическим осям имеют один и тот же коэффициент, равный 0,82.

Чтобы упростить изометрическую проекцию, по осям x, y и z, как правило, выполняют без искажений, то есть его коэффициент выбирают равным единице.

Изображение окружностей в прямоугольной изометрии

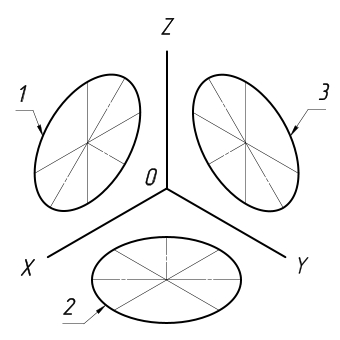
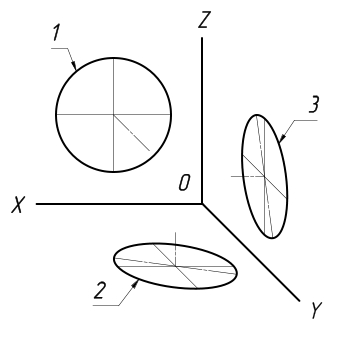
Если окружности располагаются в тех плоскостях, которые параллельны плоскостям проекций, то в аксонометрической плоскости они изображаются в виде эллипсов.

В тех случаях, когда по осям x, y, и z изометрическая проекция выполняется без искажений, длина большой и малой осей эллипсов составляет, соответственно, 1,22 и 0,71 от диаметра отображаемой окружности.

В тех случаях, когда по осям x, y и z изометрическая проекция выполняется с искажениями, длина большой оси эллипсов равняется диаметру отображаемой окружности, а длина малой оси – 0,58 от нее.

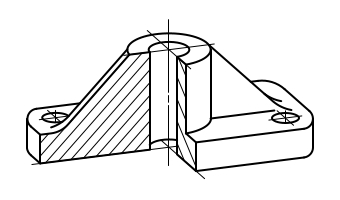
Изображение детали в прямоугольной изометрии

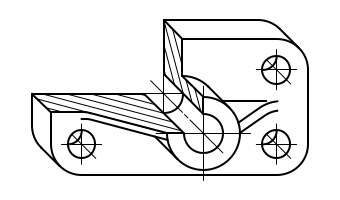
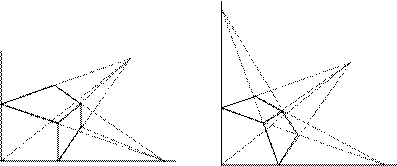
Чтобы наиболее наглядно передать особенности формы различных изделий и предметов, их изображают в прямоугольной изометрической проекции.

Прямоугольная диметрическая проекция

Отличительной особенностью прямоугольной диметрической проекции является то, что она имеет различные коэффициенты искажения по разным аксонометрическим осям: для x и z он имеет значение 0,94, а по y, равна значению 0,47.

В большинстве случаев диметрическая проекция выполняется с коэффициентом искажения по оси аксонометрии y, равным 0,5, и по осям аксонометрии z и x, равным единице.

Изображение окружностей в прямоугольной диметрии

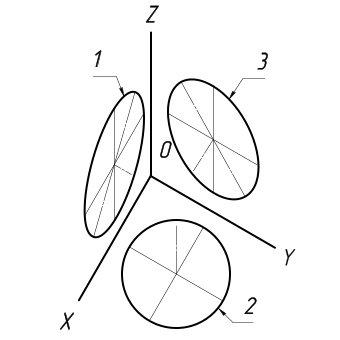
Те окружности, которые располагаются в плоскостях, являющихся параллельными по отношению к плоскости проекции, при проецировании на аксонометрическую плоскость изображаются в виде эллипсов.

В тех случаях, когда диметрическая проекция окружности выполняется в неискаженном виде по осям z и x, длина большой оси эллипсов составляет 1,06 от диаметра изображаемой окружности, при этом малая ось эллипса под номером 1 ровна 0,95, а эллипсов под номерами 2 и 3 ровна 0,35 диаметра окружности.

В тех случаях, когда диметрическая проекция окружности выполняется в искаженном виде по осям x и z, длина больших осей всех эллипсов соответствует диаметру окружности, малой оси эллипса под номером 1 равна 0,9, а эллипсов с номерами 2 и 3 равна 0,33 длины диаметров окружности.

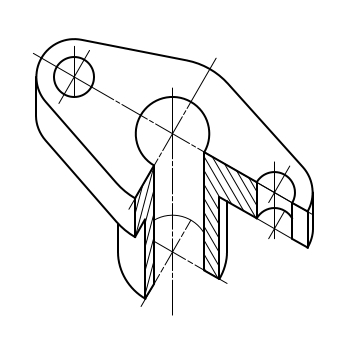
Изображение детали в прямоугольной диметрии

Для того чтобы в печатных изданиях и на некоторых других видах носителей информации представить деталь или изделие наиболее наглядно, ее изображают в прямоугольной диметрии.

Косоугольная фронтальная изометрическая проекция

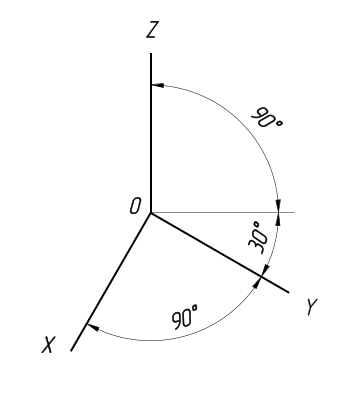
Для этой проекции характерно то, что проекции с углом наклона оси у допускается располагать с углом наклона от 30° до 60°. Фронтальная изометрическая проекция по осям x, y и z искажений не имеет.

Изображения окружности в косоугольной фронтальной изометрии

Те окружности, которые располагаются в плоскостях, лежащих параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в виде окружностей. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,3 диаметра окружности, а малой оси – 0,54 диаметра окружности.

Изображение детали в косоугольной фронтальной изометрии

Изображение деталей в косоугольной фронтальной изометрии, используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

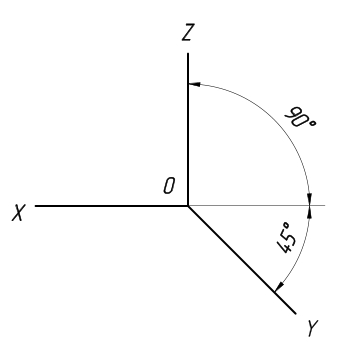
Косоугольная горизонтальная изометрическая проекция

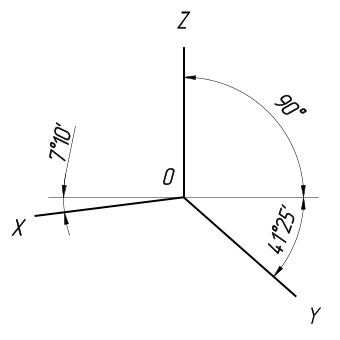
Отличительной особенностью косоугольной горизонтальной изометрической проекции является то, что здесь допускается применять, что проекции с углом наклона оси у допускается располагать под углом наклона от 45° до 60°, при этом угол 90° между осями x и y должен сохраняться неизменным. В данной проекции искажения отсутствуют по всем осям.

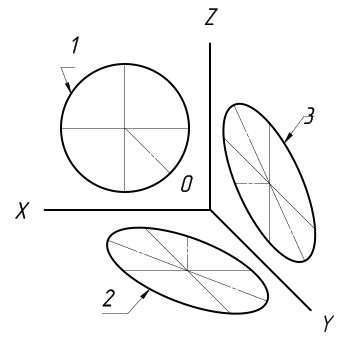
Изображения окружности в косоугольной горизонтальной изометрической проекции

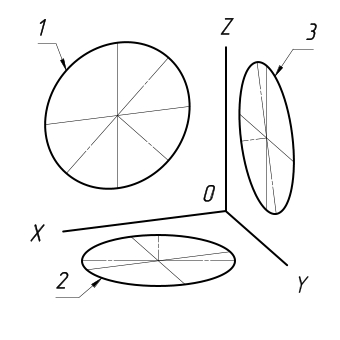
Те окружности, которые располагаются в плоскостях, находящихся параллельно горизонтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и фронтальной плоскостям проекций, проецируются в эллипсы.

Наибольшая ось эллипса под номером 1 равна 1,37, а малая ось равна 0,37 от диаметра окружности. Большая ось эллипса номер 3 равна 1,22, а малая ось равна 0,71 от диаметра окружности.

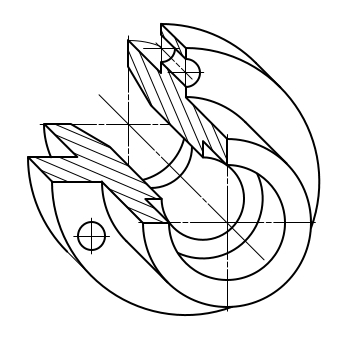
Изображение детали в косоугольной горизонтальной изометрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

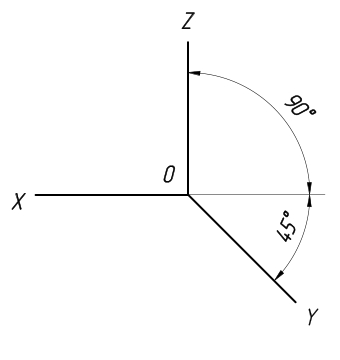
Косоугольная фронтальная диметрическая проекция

Отличительной чертой этой проекции является то, что аксометрическая ось y может иметь угол наклона от 30° до 60°. При этом коэффициент искажения по осям x и z равняется единице, а по оси y – 0,5.

Изображения окружности в косоугольной фронтальной диметрии

Те окружности, которые располагаются в плоскостях, находящихся параллельно фронтальной плоскости проекций, на аксонометрическую плоскость проецируются в окружности. Те окружности, которые располагаются в плоскостях, находящихся параллельно профильной и горизонтальной плоскостям проекций, проецируются в эллипсы. При этом длина их больших осей составляет 1,07 диаметра окружности, а малой оси – 0,33 диаметра окружности.

Изображение детали в косоугольной фронтальной диметрии

Эта проекция используется для того, чтобы наиболее наглядно передать форму изделий и предметов.

Нанесение размеров

Размерные линии при изображении аксонометрических проекций должны наноситься параллельно измеряемым отрезкам, а выносные – параллельно аксонометрическим осям.

Штриховка

Сечения во всех аксонометрических проекциях наносится штриховкой. При этом ее линии должны быть параллельны лежащим в соответствующих координатных плоскостях диагоналям проекций квадратов.

Источник

Изометрия и диметрия

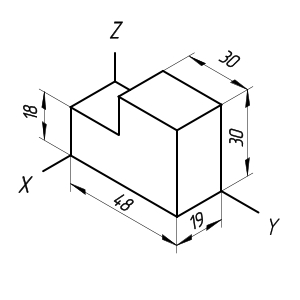
В изометрической проекции координатные оси объекта отображаются на визуальную плоскость под углом 1200, а масштабные коэффициенты по всем трем осям одинаковы.

Для диметрической проекции оси Y и X проецируются параллельно осям Y* и X* визуальной плоскости, а проекция оси Z совпадает с биссектрисой угла между осями Y* и X*. Причем коэффициент искажения по оси Z равен ½ (отношение длины проекции к длине отрезка).

Таким образом, матрица изометрического проецирования Qи и матрица диметрического проецирования Qд имеют вид:

Перспективные проекции

Предположим, что центр проецирования лежит на оси Z в точке «с» (0,0,с) и плоскость проецирования совпадает с координатной плоскостью Y/X. Возьмем в пространстве произвольную точку и проведем через нее и точку «с» прямую.

Тогда

Матрица перспективного преобразования записывается в виде: ,

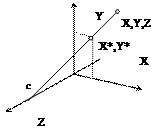
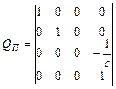
где точка «с» называется точкой схода.

В общем виде, когда оси координатной системы не параллельны визуальной плоскости, матрица QП содержит три точки схода (-a,0,0), (0,-b,0) и (0,0,-c) на осях X, Y и Z соответственно, т.е. всего может быть не более 3-х точек схода (по одной на каждой оси). В этом случае матрица QП имеет вид:

.

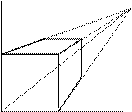
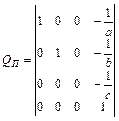
Работу глаза можно описать достаточно точно геометрически, однако зрительное восприятие не создается только глазом. Зрительное восприятие в большей степени создается мозгом. Он «расширяет», «сжимает» с различной интенсивностью разные фрагменты изображений, получаемых на сетчатке, и создает образ 3-х мерного пространства. Этот образ позволяет человеку оценивать расстояние до предметов, их высоту, глубину и т.п.

Наблюдатель находится на оси Z и направление проецирования проходит через точку, находящуюся в плоскости Y/X на расстоянии L от начала координат на прямой, образующей с осью Х угол a, и составляет угол b с плоскостью Y/X.

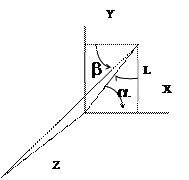
Матрица, описывающая косоугольное проецирования, имеет вид:

.

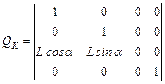
Применение матрицы QК приводит к сдвигу и последующему проецированию. Точки с координатой z переносятся в направлении Х на zLcosa и в направлении y на zLsina, и затем осуществляется ортографическое проецирование на плоскость z=0. Сдвиг сохраняет параллельность прямых, а также углы и расстояния в плоскостях, параллельных оси z=0.

Для свободной проекции L=1, а угол b=45°. Для кабинетной проекции L=1/2, а b=arctg(2)=63,4°.

Ортографическое проектирование есть частный случай косоугольного проецирования (L=0 и b=90°).

Рассмотренные матрицы преобразований не всегда позволяют получить полное представление о предмете. Поэтому в системах 3_х мерной графики нет необходимости фиксировать какие-либо конкретные виды проекций. Для наиболее полного представления о предмете чаще используют операции вращения предмета вокруг двух или трех осей. Например, матрица

Одной из определяющих проблем на пути создания реалистических изображений является проблема закрашивания поверхностей, ограничивающих построенные объекты. Мы остановимся на описании некоторых простейших моделей, требующих сравнительно небольших вычислительных затрат.

Световая энергия, падающая на поверхность от источника света, может быть поглощена, отражена и пропущена. Количество поглощенной, отраженной и пропущенной энергии зависит от длины световой волны. При этом цвет поверхности объекта определяется поглощаемыми длинами волн.

Свойства отраженного света зависят от формы и направления источника света, а также от ориентации освещаемой поверхности и ее свойств. Свет, отраженный от объекта, может быть диффузным и зеркальным: диффузно отраженный свет рассеивается равномерно по всем направлениям, зеркальное отражение происходит от внешней поверхности объекта.

Свет точечного источника отражается от идеального рассеивателя по закону косинусов Ламберта:

, (1)

где — интенсивность отраженного света; — интенсивность точечного источника; — коэффициент диффузного отражения (постоянная величина, ); — угол между направлением на источник света и (внешней) нормалью к поверхности ( , рис. 1).

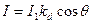
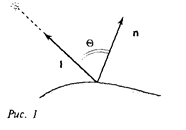
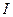
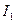
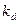
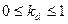
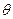
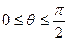
На объекты реальных сцен падает еще и рассеянный свет, соответствующий отражению света от других объектов. Поскольку точный расчет рассеянного освещения требует значительных вычислительных затрат, в компьютерной графике при вычислении интенсивности поступают так :

(2)

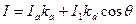
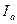
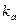
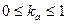
где — интенсивность рассеянного света; — (постоянный) коэффициент диффузного отражения рассеян­ного света, .

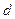
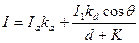
Интенсивность света, естественно, зависит от расстояния от объекта до источника света. Для того чтобы учесть это, пользуются следующей моделью освещения:

(3)

где 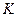— произвольная постоянная.

Интенсивность зеркально отраженного света зависит от угла падения, длины волны и свойств вещества. Так как физические свойства зеркального отражения довольно сложны, то в простых моделях освещения обычно пользуются следующей эмпирической моделью (моделью Фонга):

, (4)

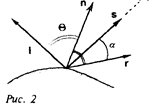
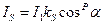
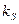
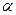
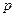
где — экспериментальная постоянная; — угол между отраженным лучом и вектором наблюдения; — степень, аппроксимирующая пространственное распределение света (рис. 2).

Объединяя последние две формулы, получаем модель освещения (функцию закраски), используемую для расчета интенсивности (или тона) точек поверхности объекта (или пикселов изображения):

(5)

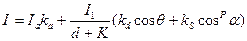
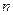
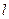
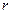
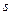
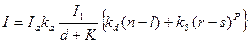
Функцию закраски, используя единичные векторы внешней нормали , а также единичные векторы, определяющие направления: на источник (вектор ), отраженного луча (вектор ) и наблюдений (вектор ), можно записать в следующем виде:

(6)

Если точечных источников света несколько, скажем m, то модель освещения определяется так

. (7)

Если освещаемая поверхность в рассматриваемой точке гладкая (имеет касательную плоскость), то вектор внешней нормали вычисляется непосредственно (рис. 3). В случае многогранной поверхности векторы внешних нормалей можно найти только для ее граней. Что касается направлений векторов внешних нормалей на ребрах и в вершинах этой поверхности, то их значения можно найти только приближенно.

Пусть, например, граней, сходящиеся в данной вершине, имеют нормали , где , являются векторами внешних нормалей для рассматриваемой многогранной поверхности (рис. 4).

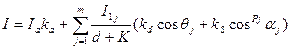
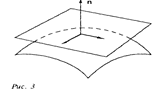
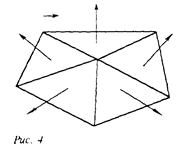
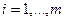
Вектор в вершине получаем путем усреднением нормалей граней:

.

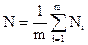
Закраска методом Гуро

Наиболее простым из таких методов является метод Гуро, который основывается на определении освещенности грани в ее вершинах с последующей билинейной интерполяцией получившихся величин на всю грань.

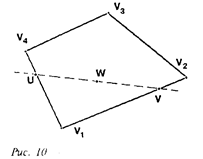
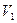
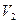
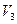
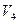
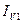
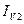
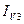
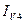
Обратимся к рис. 10, на котором изображена выпуклая четырехугольная грань. Предположим, что интенсивности в ее вершинах , , , известны и равны соответственно , , , .

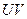
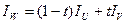
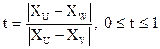
Будем считать, что интенсивность на отрезке изменяется линейно, то есть

, где .

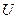
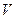
Для определения интенсивности в точках и вновь воспользуемся линейной интерполяцией, также считая, что вдоль каждого из ребер границы интенсивности изменяются линейно.

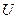
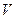
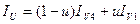
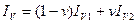
Тогда интенсивность в точках и вычисляется по формулам:

,

,

где , .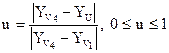

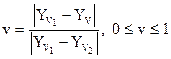
Метод Гуро обеспечивает непрерывное изменение интенсивности при переходе от одной грани к другой без разрывов и скачков.

Еще одним преимуществом этого метода является его инкрементальный характер: грань рисуется в виде набора горизонтальных отрезков, причем так, что интенсивность последующего пиксела отрезка отличается от интенсивности предыдущего на постоянную величину для данного отрезка. Кроме того, при переходе от отрезка к отрезку значения интенсивности в его концах также изменяются линейно.

Таким образом, процесс рисования грани слагается из следующих шагов:

1) проектирование вершин грани на экран и вычисление нормалей для каждой грани;

2) вычисление нормалей в вершинах граней как усреднение нормалей граней;

3) отыскание интенсивностей в вершинах согласно выбранной модели освещения;

4) определение координат концов очередного отрезка и значений интенсивности в них линейной интерполяцией;

5) рисование отрезка с линейным изменением интенсивности между его концами.

Замечания:

1. При определении освещенности в вершине, естественно, встает вопрос о выборе нормали. Часто в качестве нормали в вершине выбирается нормированная сумма нормалей прилегающих граней

2. Дефекты изображения, возникающие при закраске Гуро, частично объясняются тем, что этот метод не обеспечивает гладкости изменения интенсивности.

Закраска методом Фонга

Как и описанный выше метод закраски Гуро, закраска Фонга при расчете интенсивности также опирается на интерполирование. Однако в отличие от метода Гуро здесь интерполируется не значение интенсивности по уже известным ее значениям в опорных точках, а значение вектора внешней нормали, которое затем используется для вычисления интенсивности пиксела. Поэтому закраска Фонга требует заметно большего объема вычислений. Правда, при этом и изображение получается более близким к реалистичному (в частности, при закраске Фонга зеркальные блики выглядят довольно правдоподобно).

Метод Фонга заключается в построении для каждой точки вектора, играющего роль вектора внешней нормали, и использовании этого вектора для вычисления освещенности в рассматриваемой точке по формуле (5). При этом схема интерполяции, используемая при закраске Фонга, аналогична интерполяции в закраске Гуро.

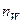
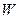
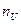
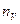
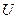
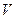
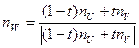
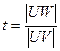
Для определения вектора «нормали» в точке проводим через эту точку горизонтальную прямую и, используя значения векторов «нормалей» и в точках ее пересечения и с ребрами грани, получаем

, где ,

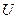
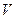
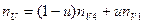
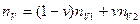
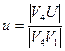
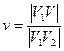
а векторы внешних нормален в точках и находятся, в свою очередь (также линейной интерполяцией), по векторам нормалей в концевых точках соответствующих ребер рассматриваемой многоугольной грани:

,

, где , .

Нормирование вектора 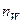необходимо в следствии того, что в формулах (1)-(5) используется единичный вектор нормали.

Замечания:

1. Как и метод Гуро метод Фонга также в значительной степени носит инкрементальный характер.

2. Применяя метод Фонга, мы фактически строим на многогранной модели непрерывное поле единичных векторов, использование которого в качестве поля внешних нормалей обеспечивает гладкость получаемого изображения.

3. Ясно, что требования к качеству изображения напрямую связаны с точностью рассматриваемой модели и объемом соответствующих ей вычислений. Несомненным достоинством предложенных моделей закраски (Гуро и Фонга) является их сравнительная простота. Однако вследствие значительных упрощений получаемый результат не всегда оказывается удовлетворительным. Преодолевать этот барьер качества лучше всего путем использования более совершенных моделей и методов.

Существуют разные способы моделирования текстуры, но практически все они подразделяются на два основных класса:

Представим себе, что необходимо задать определенную текстуру (например, мрамор) какому-либо объекту.

1. Взять изображение реальной мраморной поверхности и отобразить (спроектировать) его каким-либо образом на поверхность объекта. То есть перевести исходные трехмерные координаты точки в двумерные и использовать последние для индексации в изображение.

2. Построить некоторую функцию С(х, у, z), определяющую для каждой точки пространства (х, у, z) цвет таким образом, чтобы объект, цвет которого задается этой функцией, имел вид объекта, сделанного из мрамора.

Первый путь соответствует проективным текстурам. Он наиболее прост, однако имеет целый ряд существенных недостатков: требует большого объема памяти для хранения используемых изображений, обладает сравнительно небольшой гибкостью и к тому же сопряжен с большими сложностями в подборе способа проектирования для объектов сложной формы.

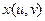
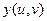
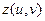
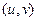
Поэтому в практических задачах, как правило, используется лишь небольшое количество стандартных вариантов проектирования: плоское (параллельное проектирование вдоль заданного направления), цилиндрическое и сферическое. Для параметрически заданных поверхностей часто в качестве проекции точки ( , , )выступают значения параметров .

Второй путь не требует больших затрат памяти и одинаково хорошо работает с объектами любой (сколь угодно сложной) формы. Поскольку подобная функция обычно зависит от большого количества параметров, то, изменяя их, можно легко изменять параметры текстуры. Основным недостатком этого подхода является сложность подбора соответствующей функции.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник