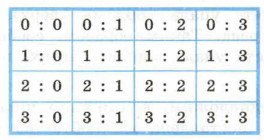
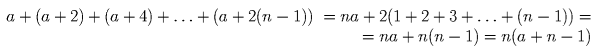Известно что 20 партий между футбольными командами
2.1. Содержательный подход к измерению информации

Здесь первая цифра в каждой паре соответствует количеству мячей, забитых командой «Спартак», вторая — командой «Динамо».
Будем считать все варианты равновероятными и отгадывать счёт, задавая вопросы, на которые можно ответить только «да» или «нет». Вопросы будем формулировать так, чтобы количество возможных вариантов счёта каждый раз уменьшалось вдвое. Это позволит нам:
1) обойтись минимальным количеством вопросов;
2) подсчитать, сколько бит информации содержит сообщение о счёте матча.
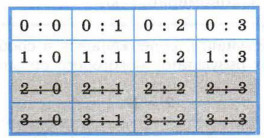
Вопрос 1. «Спартак» забил больше одного мяча? Предположим, получен ответ «Нет». Такой ответ позволяет не рассматривать варианты, расположенные в нижней части таблицы, т. е. сокращает количество возможных исходов в 2 раза:
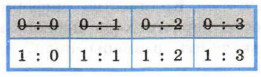
Вопрос 2. «Спартак» забил один мяч? Предположим, получен ответ «Да». Такой ответ позволяет не рассматривать варианты, расположенные в верхней строке таблицы, т. е. сокращает количество возможных исходов ещё в 2 раза:
Вопрос 3. «Спартак» пропустил больше одного мяча? Предположим, получен ответ «Нет». Можно отбросить ещё два варианта:
Вопрос 4. «Спартак» пропустил один мяч? Предположим, получен ответ «Да». Получаем единственный вариант:
Итак, нам удалось выяснить счёт матча, задав четыре вопроса, ответ на каждый из которых уменьшал неопределённость результата в два раза, т. е. нёс 1 бит информации. Сообщение о счёте матча несёт четыре бита информации.

1) Да — Да — Да — Да;
2) Нет — Нет — Нет — Нет;
3) Да — Нет — Да — Нет.
Попробуйте придумать такие вопросы, чтобы цепочка ответов Нет — Да — Нет — Да приводила к счёту 2 : 3.
Вычислять количество информации, содержащееся в сообщении о том, что имел место один из множества равновероятных результатов некоторого события, с помощью метода половинного деления возможно, но затруднительно. Гораздо проще воспользоваться следующей закономерностью.

2′ = N.
При N, равном целой степени двойки (2, 4, 8, 16, 32 и т. д.), это уравнение легко решается в уме. Решать такие уравнения при других N вы научитесь чуть позже, в курсе математики 11 класса.

Известно что 20 партий между футбольными командами
Задача 1:
В мешке лежат шарики двух разных цветов: черного и белого. Какое наименьшее число шариков нужно вынуть из мешка вслепую так, чтобы среди них заведомо оказались два шарика одного цвета?
Решение:
Обозначим первое из этих чисел через a. Получим
Задача 2:
В лесу растет миллион елок. Известно, что на каждой из них не более 600000 иголок. Докажите, что в лесу найдутся две елки с одинаковым числом иголок.
Решение:
Перед нами миллион «кроликов»-елок и, увы, всего лишь 600001 клетка с номерами от 0 до 600000. Каждый «кролик»-елка сажается нами в клетку с номером, равным количеству иголок на этой елке. Так как «кроликов» гораздо больше, чем клеток, то в какой-то клетке сидит по крайней мере два «кролика» – если бы в каждой сидело не более одного, то всего «кроликов»-елок было бы не более 600001 штук. Но ведь, если два «кролика»-елки сидят в одной клетке, то количество иголок у них одинаково.
Задача 3:
Дано 12 целых чисел. Докажите, что из них можно выбрать два, разность которых делится на 11.
Решение:
Остатки по модулю 11 – «клетки», числа – «кролики».
Задача 4:
В городе Ленинграде живет более 5 миллионов человек. Докажите, что у каких-то двух из них одинаковое число волос на голове, если известно, что у любого человека на голове менее миллиона волос.
Решение:
Постройте миллион клеток с номерами от 0 до 999999 и рассадите там людей, поместив каждого ленинградца в клетку, номер которой равен количеству волос на его голове.
Задача 5:
В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта.
Решение:
25 ящиков-«кроликов» рассадим по 3 клеткам-сортам. Так как 25 = 3 8 + 1, то применим «обобщенный принцип Дирихле» для N = 3, k = 8 и получим, что в какой-то клетке-сорте не менее 9 ящиков.
Задача 6:
В стране Курляндии m футбольных команд (по 11 футболистов в каждой). Все футболисты собрались в аэропорту для поездки в другую страну на ответственный матч. Самолет сделал 10 рейсов, перевозя каждый раз по m пассажиров. Еще один футболист прилетел к месту предстоящего матча на вертолете. Докажите, что хотя бы одна команда была целиком доставлена в другую страну.
Решение:
Так как перевезено всего 10m + 1 футболистов, то, рассадив их по клеткам-командам, получаем, что в какой-то клетке сидит 11 футболистов.
Задача 7:
Дано 8 различных натуральных чисел, не больших 15. Докажите, что среди их положительных попарных разностей есть три одинаковых.
Решение:
Различных разностей может быть 14 – от 1 до 14 – это те 14 клеток, в которые мы будем сажать кроликов. Кто же будет нашими кроликами? Ими, конечно, должны быть разности между парами данных нам натуральных чисел. Однако имеется 28 пар и их можно рассадить по 14 клеткам так, что в каждой клетке будет сидеть ровно два «кролика» (и значит, в каждой меньше трех). Здесь надо использовать дополнительное соображение: в клетке с номером 14 может сидеть не более одного кролика, ведь число 14 можно записать как разность двух натуральных чисел, не превосходящих 15, лишь одним способом: 14 = 15 – 1. Значит, в оставшихся 13 клетках сидят не менее 27 кроликов, и применение обобщенного принципа Дирихле дает нам желаемый результат.
Задача 8:
Докажите, что в любой компании из 5 человек есть двое, имеющие одинаковое число знакомых в этой компании.
Решение:
Вариантов числа знакомых всего 5: от 0 до 4. Осталось заметить, что если у кого-то 4 знакомых, то ни у кого не может быть 0 знакомых.
Задача 9:
Несколько футбольных команд проводят турнир в один круг. Докажите, что в любой момент турнира найдутся две команды, сыгравшие к этому моменту одинаковое число матчей.
Решение:
Пусть всего команд n. Тогда вариантов числа команд, с которыми сыграла данная команда n: от 0 до n – 1. Осталось заметить, что если одна команда сыграла со всеми n – 1-й, то никакая другая команда не могла ни с кем не сыграть.
Задача 10:
а) Какое наибольшее число полей на доске 8 × 8 можно закрасить в черный цвет так, чтобы в любом уголке вида из трех полей было по крайней мере одно незакрашенное поле?
б) Какое наименьшее число полей на доске 8 × 8 можно закрасить в черный цвет так, чтобы в каждом уголке вида было по крайней мере одно черное поле?
Решение:
а) Разбейте доску на 16 квадратиков 2 × 2 – это клетки; кроликами, конечно, будут черные поля.
Задача 11:
10 школьников на олимпиаде решили 35 задач, причем известно, что среди них есть школьники, решившие ровно одну задачу, школьники, решившие ровно две задачи и школьники, решившие ровно три задачи. Докажите, что есть школьник, решивший не менее пяти задач.
Решение:
Из условий следует, что найдутся 7 школьников, решивших 35 – 6 = 29 задач. Так как 29 = 4 7 + 1, то найдется школьник, решивший не менее пяти задач.
Задача 12:
Какое наибольшее число королей можно поставить на шахматной доске так, чтобы никакие два из них не били друг друга?
Решение:
Ответ: 16 королей. Разобьём доску на 16 квадратиков, в каждом может быть не более одного короля.
Задача 14:
Докажите, что равносторонний треугольник нельзя покрыть двумя меньшими равносторонними треугольниками.
Решение:
Каждый из меньших треугольников не может накрывать более одной вершины большого треугольника.
Задача 15:
В квадрат со стороной 1 метр бросили 51 точку. Докажите, что какие-то три из них можно накрыть квадратом со стороной 20 см.
Решение:
Разобьем наш квадрат на 25 квадратов со стороной 20 см. По обобщенному принципу Дирихле, в какой-то из них попадет по крайней мере три точки из 51 брошенной.
Задача 16:
Пятеро молодых рабочих получили на всех зарплату – 1500 рублей. Каждый из них хочет купить себе магнитофон ценой 320 рублей. Докажите, что кому-то из них придется подождать с покупкой до следующей зарплаты.
Решение:
Если бы каждый из рабочих мог купить магнитофон, то у них в сумме было бы не менее 5 320 = 1600 рублей.
Задача 17:
В бригаде 7 человек и их суммарный возраст – 332 года. Докажите, что из них можно выбрать трех человек, сумма возрастов которых не меньше 142 лет.
Решение:
Покрасим всю сушу в синий цвет, а все точки, диаметрально противоположные суше – в красный. Тогда обязательно есть точка, которая покрашена в оба цвета. В ней и надо рыть туннель.
Задача 19:
Докажите, что среди степеней двойки есть две, разность которых делится на 1987.
Решение:
Рассмотрите 1988 степеней и их остатки по модулю 1987.
Задача 20:
Докажите, что из 52 целых чисел всегда найдутся два, разность квадратов которых делится на 100.
Решение:
Квадраты при делении на 100 могут давать лишь 51 остаток, так как остатки x и 100 – x при возведении в квадрат дают один и тот же остаток.
Задача 21:
Докажите, что среди чисел, записываемых только единицами, есть число, которое делится на 1987.
Решение:
Рассмотрим 1988 чисел-«кроликов» 1, 11, 111, …, 111 … 11 (1988 единиц) и посадим их в 1987 клеток с номерами 0, 1, 2, …, 1986 – каждое число попадает в клетку с номером, равным остатку от деления этого числа на 1987. Тогда (по принципу Дирихле) найдутся два числа, которые имеют одинаковые остатки при делении на 1987. Пусть это числа 11 … 11 (m единиц) и 11 … 11 (n единиц), причем m > n. Но их разность, которая делится на 1987, равна 11 … 1100 … 00 (m – n единиц и n нулей). Сократим все нули – ведь они не имеют никакого отношения к делимости на 1987 – и получим число из одних единиц, которое делится на 1987.
Задача 22:
Докажите, что существует степень тройки, оканчивающаяся на 001.
Решение:
Если 3 m и 3 n – степени тройки, дающие один и тот же остаток при делении на 1000, то 3 m – 3 n = 3 n (3 m – n – 1) делится на 1000 (мы считаем для определенности, что m > n).
Задача 23:
В клетках таблицы 3 × 3 расставлены числа – 1, 0, 1. Докажите, что какие-то две из 8 сумм по всем строкам, всем столбцам и двум главным диагоналям будут равны.
Решение:
Эти суммы могут принимать лишь 7 разных значений: от – 3 до 3.
Задача 24:
Сто человек сидят за круглым столом, причем более половины из них – мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга.
Решение:
Разобьем всех людей на 50 пар так, что в каждой паре – два человека, сидящих друг напротив друга. Ясно, что в одной из этих пар-«клеток» оба человека – мужчины.
Задача 25:
15 мальчиков собрали 100 орехов. Докажите, что какие-то два из них собрали одинаковое число орехов.
Решение:
Если это не так, то, очевидно, что мальчики собрали не менее, чем 0 + 1 + 2 + … + 14 = 105 орехов – противоречие.
Задача 26:
Цифры 1, 2, …, 9 разбили на три группы. Докажите, что произведение чисел в одной из групп не меньше 72.
Решение:
Произведение чисел во всех группах равно 9! = 362880, а 71³ = 357911.
Задача 27:
В таблице 10 × 10 расставлены целые числа, причем любые два числа в соседних клетках отличаются не более, чем на 5. Докажите, что среди этих чисел есть два равных.
Решение:
Поскольку от любой клетки до любой другой можно добраться, не более 19 раз сдвинувшись в соседнюю клетку, то все числа находятся между числами a и a + 95, где a – минимальное из всех расставленных чисел. Значит, среди этих чисел не более 96 различных.
Задача 28:
Докажите, что среди любых 6 человек есть либо трое попарно знакомых, либо трое попарно незнакомых.
Решение:
У данного человека среди остальных пяти есть либо не менее трех знакомых, либо не менее трех незнакомых ему. Разберем, например, первый случай. Среди этих трех людей есть либо двое знакомых – тогда они вместе с выбранным нами исходно человеком образуют нужную тройку, либо они все трое попарно незнакомы.
Задача 29:
На клетчатой плоскости дано 5 произвольных узлов сетки. Докажите, что середина одного из отрезков, соединяющих какие-то две из этих точек, также является узлом сетки.
Решение:
Рассмотрите координаты этих точек и их остатки при делении на 2.
Задача 30:
На складе имеется по 200 сапог 41, 42 и 43 размеров, причем среди этих 600 сапог 300 левых и 300 правых. Докажите, что из них можно составить не менее 100 годных пар обуви.
Решение:
В каждом размере каких-то сапог меньше: правых или левых. Выпишем эти типы сапог по размерам. Какой-то тип, например, левый, повторится по крайней мере дважды, например, в 41 и 42 размерах. Но так как количество левых сапог в этих размерах суммарно не меньше 100 (почему?), то мы имеем не менее 100 годных пар обуви в этих размерах.
Задача 31:
В алфавите языка племени Ни-Бум-Бум 22 согласных и 11 гласных, причем словом в этом языке называется произвольное буквосочетание, в котором нет двух согласных подряд и ни одна буква не использована дважды. Алфавит разбили на 6 непустых групп. Докажите, что из всех букв одной из групп можно составить слово.
Решение:
Докажите, что в одной из групп разность между числом согласных и числом гласных не больше 1.
Задача 32:
Докажите, что среди любых 10 целых чисел найдется несколько, сумма которых делится на 10.
Решение:
Задача 33:
Дано 11 различных натуральных чисел, не больших 20. Докажите, что из них можно выбрать два числа, одно из которых делится на другое.
Решение:
Разбейте числа от 1 до 20 на 10 наборов, в каждом из которых в любой паре чисел одно делится на другое: 11, 13, 15, 17, 19, 1,2,4,8,16, 3,6,12, 5,10,20, 7,14, 9,18.
Задача 34:
11 пионеров занимаются в пяти кружках дома культуры. Докажите, что найдутся два пионера А и В такие, что все кружки, которые посещает А, посещает и В.
Решение:
Занумеруем кружки числами от 1 до 5 и вместо каждого пионера будем рассматривать тот набор кружков – подмножество множества 1,2,3,4,5 – который состоит из посещаемых им кружков. Осталось разбить 32 подмножества указанного множества на 10 наборов так, чтобы в каждом из наборов из любых двух множеств этого набора одно содержалось в другом. В качестве таких наборов рассмотрим следующие: 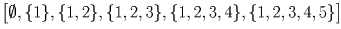
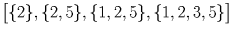
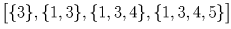
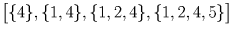
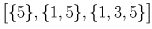
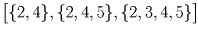
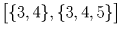
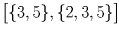
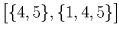
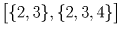
Известно что 20 партий между футбольными командами
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Химик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Химик» выиграет жребий ровно два раза.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Химика», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 2 3 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Сапфир», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 2 3 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Сапфир» начнёт игру с мячом не более одного раза.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Сапфиром», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций четыре: 000, 001, 010, 100, а всего комбинаций 2 3 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна: