какие колебания являются свободными
Свободные колебания – примеры, виды
Колебательные процессы широко распространены в природе. Одним из видов таких процессов являются свободные колебания. Рассмотрим их особенности.
Колебания и их виды
Колебания – это изменение состояния системы вокруг некоторого положения равновесия. Для возникновения колебаний необходим первоначальный импульс. А дальнейшее поведение системы может быть различным. В одних случаях сразу после прекращения воздействия система приходит в равновесие. И тогда, чтобы в системе продолжали происходить колебания, необходимо постоянно совершать работу по изменению состояния системы.
В других случаях система, выведенная из равновесия, не сразу приходит в исходное состояние, а совершает много колебательных движений, несмотря на то, что внешнее воздействие давно закончилось.
Описанные два вида колебаний называются соответственно вынужденными и свободными.
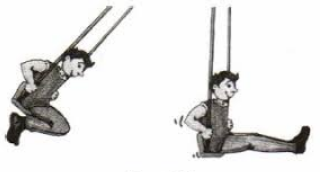
Вынужденные колебания – это колебания, совершаемые под действием внешней силы (поршень в двигателе). Свободные колебания – это колебания, совершаемые под действием внутренних сил системы (маятник).
Рис. 1. Свободные и вынужденные колебания.
Условия возникновения свободных колебаний
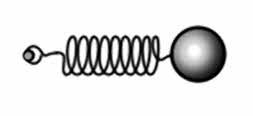
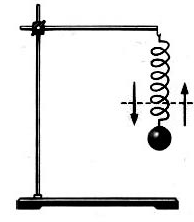
Условия возникновения свободных колебаний можно проследить на примере пружинного маятника. Такой маятник представляет собой груз, подвешенный на пружине.
Рис. 2. Пружинный маятник.
В положении равновесия пружина немного растянута, компенсируя вес груза (либо не имеет растяжения, если маятник горизонтален). При выведении из положения равновесия, в пружине возникает сила, тем большая, чем сильнее отклонение, и груз начнет движение.
Однако, в момент достижения точки равновесия, груз будет иметь некоторую скорость и кинетическую энергию. Остановиться здесь он не сможет. Он продолжит движение дальше, замедляясь и создавая в пружине новое напряжение, направленное в сторону, противоположную отклонению. В момент, когда он остановится – пружина вновь будет сжата, и снова начнет толкать груз к положению равновесия.
Таким образом, мы видим три условия, необходимых для возникновения свободных колебаний:
Есть еще одно, менее очевидное условие. Если пружинный маятник окажется в сильновязкой жидкости, то даже если вывести его из положения равновесия, груз медленно вернется в равновесие, и колебания не возникнут. Причина в том, что энергия сжатой пружины будет истрачена не на разгон груза, а на преодоление сопротивления вязкой жидкости.
Таким образом, последнее условие возникновения свободных колебаний – потери в системе должны быть достаточно малы, чтобы энергия, возвращающая систему в положение равновесия, терялась медленно.
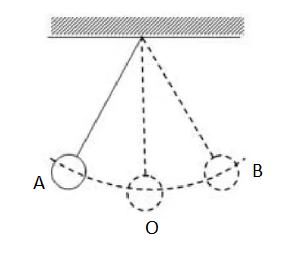
Примерами свободных колебаний является не только пружинный маятник, но и обычный маятник (качели), часовой балансир, натянутая звенящая струна, прыгающий мяч и многое другое.
в зависимости от ситуации свободные колебания в системе могут быть желательны, а могут быть вредны. Если свободные колебания желательны (часовой маятник) – то принимают все меры для уменьшения потерь. Если свободные колебания вредны (детали машин и механизмов) – то вводят элементы, увеличивающие потери – демпферы и амортизаторы.
Рис. 3. Амортизаторы.
Что мы узнали?
Свободные колебания – это колебания, совершаемые под действием внутренних сил системы. Для их возникновения необходимо, чтобы в системе было одно положение равновесия, из которого система была бы выведена, чтобы возникала сила, возвращающая систему в равновесие, и чтобы потери в системе были достаточно малы.
Колебательное движение. Свободные колебания
Урок 22. Физика 9 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Колебательное движение. Свободные колебания»
Своеобразные движения, которые называются колебательными или просто колебаниями, всем вам хорошо известны. Они широко распространены в окружающем нас мире. Колеблются ветки деревьев и трава во время ветра, колеблется корабль на волнах, крылья бабочки и так далее.
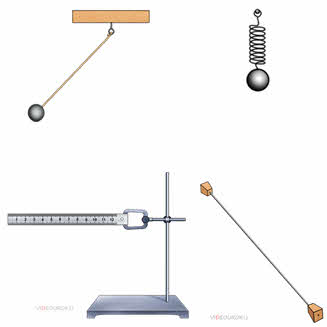
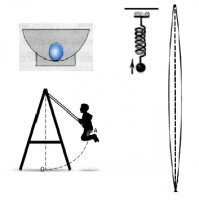
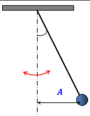
Или вот ещё примеры. На рисунке представлены тела, которые способны совершать колебания, если их отклонить от положения равновесия.
Конечно же колебания этих тел будут различными. Так, шарик, подвешенный на нити, движется по дуге окружности, а тот же шарик, подвешенный на резиновом шнуре, может совершать колебания в вертикальной плоскости. Наконец, верхний конец линейки движется с большим размахом, чем средняя точка струны. При этом каждое из этих тел может за одно и тоже время совершить разное число колебаний. Но при всём разнообразии этих движений у них есть одна общая и очень важная черта: через определённый промежуток времени движение любого из этих тел повторяется.
На самом деле, если мы отклоним шарик на нити от положения устойчивого равновесия и отпустим его, то он, пройдя положение равновесия, отклониться от в другую сторону, на мгновение остановится и вернётся в точку начала движения. При отсутствии сил сопротивления, такое движение будет повторяться бесконечно долго.
Такие колебания называются периодическими. А промежуток времени, в течение которого движение тела повторяется, называется периодом колебаний.
Таким образом, механическим колебанием называется процесс, при котором какая-либо физическая величина, характеризующая этот процесс, последовательно изменяется то в одну, то в другую сторону около своего положения равновесия.
Именно такие колебания мы и будем изучать с вами в дальнейшем.
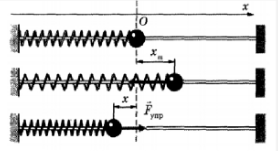
Давайте более подробно рассмотрим процесс колебаний на примере металлического шарика, прикреплённого к пружине. Шарик надет на тонкий металлический стержень и может свободно по нему скользить.
Пружина пока не деформирована, так что на тело сила упругости не действует. Будем считать, что сила трения между шариком и стержнем пренебрежимо мала. А сила тяжести уравновешена силой реакции стержня. Следовательно, вся система находится в состоянии равновесия. Направим координатную ось Ох параллельно стержню, а за начало отсчёта примем центр тяжести тела в положении равновесия.
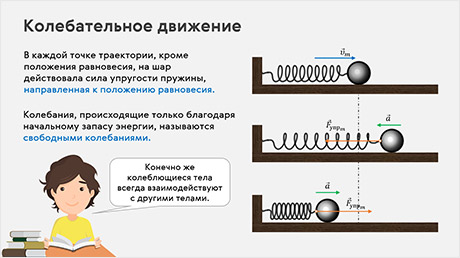
Отведём тело от положения равновесия на некоторое расстояние. Пружина при этом растянется, и на тело будет действовать сила упругости. При этом она будет тем больше, чем дальше мы будем отклонять шарик от положения равновесия, и направлена она противоположно смещению. Отпустим тело. Оно начнёт двигаться с ускорением влево, а сила упругости при этом будет уменьшаться. Дойдя до положения равновесия шарик не остановится в нем, а вследствие инерции перейдёт его и продолжит движение влево. В теле вновь возникает сила упругости, но теперь она направлена против скорости шарика и, поэтому, тормозит его. В результате в некоторой точке шарик остановиться. Теперь пружина сжата, на тело действует сила, направленная вправо, куда шарик после мгновенной остановки и начнёт двигаться. Он снова пройдёт через положение равновесия (теперь уже слева направо) и опять отклониться от него, придя в свою первоначальную точку. Таким образом, шарик совершит одно полное колебание. Причём обратите внимание на то, что в каждой точке траектории, кроме положения равновесия, на шар действовала сила упругости пружины, направленная к положению равновесия.
Под действием возвращающей силы, тело может совершать колебания как бы само по себе. Изначально эта сила возникла из-за того, что мы совершили работу по растяжению пружины, сообщив ей некоторый запас энергии. За счёт неё и происходили колебания.
Колебания, происходящие только благодаря начальному запасу энергии, называются свободными колебаниями.
Конечно же колеблющиеся тела всегда взаимодействуют с другими телами. В нашем примере это был шарик, пружина и стойка, к которой эта пружина прикреплена. В результате взаимодействия этих тел друг с другом и возникала сила, возвращающая шарик к положению равновесия.
Так вот, физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания, называют колебательной системой.
На рисунке представлена колебательная система, которая состоит из шарика, нити, штатива и Земли.
Данная система способна совершать свободные колебания под действием двух сил: силы тяжести и силы упругости нити. Равнодействующая этих сил всегда направлена к положению равновесия.
Итак, что же нужно, чтобы в системе могли возникнуть и существовать колебания?
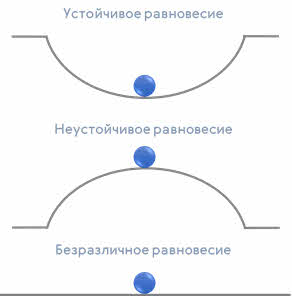
Во-первых, это наличие в системе положения устойчивого равновесия…
Вспомним, что помимо устойчивого равновесия, существует также равновесия неустойчивое и безразличное. В таких системах свободные колебания возникнуть не могут.
Во-вторых, тело должно обладать избытком механической энергии, по сравнению с его энергией в положении устойчивого равновесия. Так, в нашем примере, телу нужно сообщить избыток потенциальной энергии, то есть тело необходимо вывести из положения равновесия.
В-третьих, на тело должна действовать сила, способная вернуть тело в положение устойчивого равновесия, то есть возвращающая сила. В нашем примере, это равнодействующая силы тяжести шарика и силы реакции опоры.
И наконец, чтобы колебание возникло и продолжалось, избыточная энергия, полученная телом, не должна быть полностью израсходована на преодоление сил сопротивления при возвращении тела в положение равновесия. В идеальных колебательных системах силы трения отсутствуют, и возникшие колебания могут продолжаться бесконечно долго.
Вообще, понятие колебательной системы довольно обширное и оно применимо к разнообразным явлениям. Вы знаете, что для упрощённого рассмотрения тех или иных явлений в науке часто пользуются идеальными моделями. Для колебательных систем такими моделями являются маятники.
В общем случае маятником называется твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
Существует несколько видов маятников. Наиболее часто встречающиеся, это пружинный маятник, представляющий собой груз, прикреплённый к пружине, и способный совершать колебания вдоль горизонтальной или вертикальной оси.
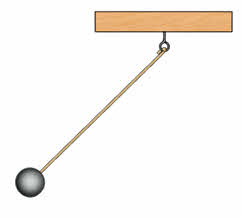
Нитяной маятник — это шарик, подвешенный на нити, способный совершать колебательное движение.
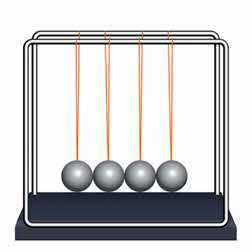
Система из нескольких шариков, подвешенных на нитях в одной плоскости, колеблющихся в этой плоскости и соударяющихся друг с другом, называется маятником (или колыбелью) Нью́тона.
Кстати, это изобретение было придумано английским актёром Саймоном Пребблом в 1967 году, для демонстрации закона сохранения импульса.
А тело, подвешенное на нити, и способное изменять плоскость своих колебаний, называется маятником Фуко.
Такой маятник используется для демонстрации суточного вращения Земли. Первый публичный показ маятника был осуществлён французским физиком Жаном Фуко́ в 1851 году в парижском Пантеоне. Под куполом Пантеона он подвесил на стальной проволоке, длиной 67 метров, 28 килограммовый шар с закреплённым на нём остриём. Под подвесом было сделано круговое ограждение диаметром 6 метров, по краю которого была насыпана песчаная дорожка так, чтобы при движении маятник прочерчивал на песке отметки. Одно колебание маятник совершал за 16,4 секунды, каждый раз отклоняясь от предыдущей отметки примерно на 3 миллиметра. Так, медленно поворачиваясь по часовой стрелке (то есть против направления вращения Земли), плоскость колебания маятника примерно за 32 часа совершала один полный оборот и возвращалась в первоначально положение.
На Северном или Южном полюсе Земли (то есть там, где ось вращения Земли лежит в плоскости колебаний маятника) плоскость колебаний маятника Фуко совершает поворот на 360 о за звёздные сутки (примерно за 23 ч 56 мин 4 с), что экспериментально подтверждает суточное вращение нашей планеты.
Свободные колебания.
Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинетической) при отсутствии внешних воздействий.
Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.
Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними образуют систему тел, которая называется колебательной системой.
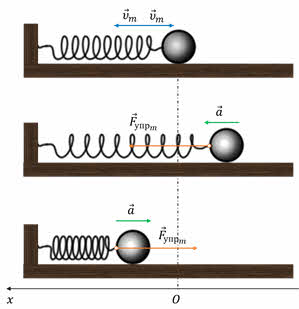
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.
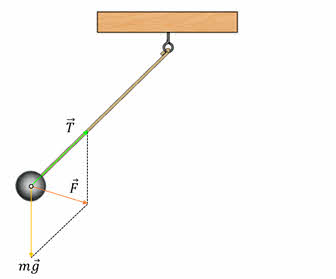
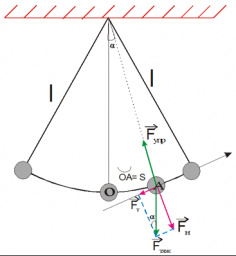
Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.
Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называются силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свободные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.
Условиями возникновения свободных колебаний являются:
1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;
2) отсутствие трения в системе.
Динамика свободных колебаний.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.
Знак минус появился потому, что сила и угол отклонения от положения равновесия α имеют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что аτ = s», окончательно получим:

Вид уравнения 

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.
Решением уравнений 

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:
В уравнении x = xm cos ω0 t (или x = xm sin ω0 t), хm — амплитуда колебания, ω0 — собственная циклическая (круговая) частота колебаний.
Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.
Для математического маятника выполняются равенства:

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).
Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.
Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятника, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.
Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = xm cos ω0 t (или x = xm sin ω0 t)), получим выражение для скорости:
где am = ω 2 0 xm — амплитуда ускорения. Таким образом, амплитуда скорости гармонических колебаний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.
Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
Примеры свободных колебаний:
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
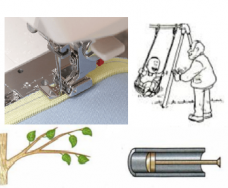
Примерами вынужденных колебаний служат:
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
где k — жесткость пружины.
Тогда уравнение движения шарики принимает
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
Начальная скорость равна нулю. Отсюда:
Максимальная скорость равна:
Уравнение движения математического маятника
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Разделим обе части выражения на массу шарика m и получим:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
Тогда длина нити равна:
Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
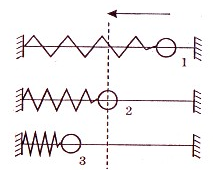
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Решение
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Решение
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить