какие математические методы применяются при экспериментальных исследованиях

Математическая обработка экспериментальных данных

К основным преимуществам вычислительного эксперимента можно отнести следующие:

• возможность исследования объекта без модификации установки или аппарата;

• возможность исследования каждого фактора в отдельности, в то время как в реальности они действуют одновременно;

• возможность исследования нереализуемых на практике процессов.

В ряде случаев именно результаты экспериментальных исследований дают толчок к теоретическому обобщению изучаемого явления. Экспериментальное исследование дает более точное соответствие между изучаемыми параметрами.

Целью данной работой является рассмотрение основных методов обработки экспериментальных данных – графический метод, метод средних и метод наименьших квадратов, а также самостоятельные решения задач по обработке опытных данных с применением вышеуказанных методов.

МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. Некоторые понятия математической статистики

Установление зависимости между двумя и более наблюдаемыми величинами является одним из основных методов математической статистики.

Статистика – функция от результатов наблюдений, являющаяся случайной величиной.

Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и исследования статистических данных для научных и практических выводов.

В своей работе я буду использовать такие понятия математической статистики, как регрессия, корреляция и коэффициент корреляции.

Регрессия – зависимость среднего значения какой-либо случайной величины от некоторой другой величины или нескольких величин.

Регрессия тесно связана с корреляцией.

Корреляция – зависимость между случайными величинами, выражающаяся в том, что распределение одной величины зависит от значения, принятого другой величиной.

Коэффициент корреляции (rxy) – числовая характеристика совместного распределения двух случайных величин x и y, выражающая их взаимосвязь. Коэффициент корреляции обладает следующим свойством:

Понятия “корреляция” и “регрессия” тесно связаны между собой. В корреляционном анализе оценивается сила связи, а в регрессионном анализе исследуется её форма. Корреляция в широком смысле объединяет корреляцию в узком смысле и регрессию.

К задачам корреляционного анализа относят:

• Измерение степени связности двух или более явлений.

• Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения связи между ними.

• Обнаружение неизвестных причинных связей. Корреляция устанавливает степень необходимости этих связей и достоверность суждений об их наличии.

К задачам регрессионного анализа относят:

• Установление формы зависимости (линейная или нелинейная, положительная или отрицательная и т. д. )

• Определение функции регрессии и установление влияния факторов на зависимую переменную.

• Оценка неизвестных значений зависимой переменной.

2. Цели математической обработки результатов эксперимента

Целью любого эксперимента является определение качественной и количественной связи между исследуемыми параметрами. В некоторых случаях вид зависимости между переменными величинами известен по результатам теоретических исследований. Как правило, формулы, выражающие эти зависимости, содержат некоторые постоянные, значения которых и необходимо определить из опыта. Другим типом задачи является определение неизвестной функциональной связи между переменными величинами на основе данных эксперимента. Такие зависимости называют эмпирическими. Однозначно определить неизвестную функциональную зависимость между переменными невозможно даже в том случае, если бы результаты эксперимента не имели ошибок. Поэтому следует четко понимать, что целью математической обработки результатов эксперимента является не нахождение истинного характера зависимости между переменными или абсолютной величины какой-либо константы, а представление результатов наблюдений в виде наиболее простой формулы с оценкой возможной погрешности ее использования.

Обычно полученные в результате наблюдений данные представляют собой набор чисел. Просматривая этот набор, довольно трудно выявить какую-либо закономерность, поэтому результаты экспериментальных исследований нуждаются в определенной математической обработке.

В своей работе я буду рассматривать три основных метода обработки экспериментальных данных:

• Метод наименьших квадратов.

2. МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

1. 2 Графический метод обработки данных

Пусть данные опыта представлены таблицей. Через точки, определяемой этой таблицей или близкие к ним, проводим график и по виду графика подбираем вид эмпирической формулы. Простейшим случаем считается тот, для которого данные опыта приводят к точкам, располагающимися приблизительно на прямой y = a0 + a1x или на кривых, уравнения которых

S = Atα и S = Aeαt преобразуются заменой переменных к линейной функции. Решая эту задачу графическим способом, наносим точки на координатную сетку (с равномерной или логарифмической шкалой) и проводим прямую приблизительно через эти точки, так, чтобы она лежала возможно ближе к каждой из нанесенных точек, а затем берем две произвольные точки на этой прямой (совершенно произвольно) и подставляем их координаты в соотношении y = a0 + a1x. Из полученных таким образом двух уравнений найдем a0 и a1.

Уклонение – расстояние между приближаемой и приближающей функциями.

Способ средних основывается на допущении, что наиболее подходящей линией служит та, для которой алгебраическая сумма уклонений равна нулю. Для этого чтобы найти этим способом неизвестные постоянные в эмпирической формуле, сначала подставляем в эту формулу все пары наблюдавшихся или замеренных значений x и y и получаем столько уклонений, сколько пар значений (x;y) в таблице (уклонения – вертикальные расстояния от данных точек до графика функции). Затем распределяем эти уклонения по группам, составляя столько групп, сколько неизвестных параметров эмпирической формулы надо найти. Наконец, приравнивая нулю сумму уклонений по каждой группе, получим систему линейных уравнений относительно параметров.

2. 3 Метод наименьших квадратов.

Которая наилучшим образом выражает зависимость Y от X. Для нахождения такой функции пользуются методом наименьших квадратов.

Пусть даны n пар чисел:

Требуется найти такую прямую, чтобы сумма квадратов “отклонений” этих точек от прямой (3. 1) была как можно меньше. Значит, выражение

2 (2. 2) должно быть минимальным.

Отклонения (рис. 2. 1) изображены в виде вертикальных отрезков (перпендикуляров).

Выражение (2. 2) является функцией двух переменных a и b. Можно сказать, что выражение (2. 2) принимает минимальное значение, если величины a и b связаны соотношениями (полное выведение см. в )

Эта система имеет единственное решение:

Найдя неизвестные a и b, мы найдем тем самым прямую (2. 1), наилучшим образом выражающую статистическую связь между величинами X и Y. Полученная прямая называется прямой регрессии Y на X.

Стационарное распределение температуры в теплоизолированном тонком стержне описывается линейной функцией u = a0 +a1x. Определить постоянные a0 и a1, если дана таблица измеренных температур в соответствующих точках стержня:

Число зрителей (в тыс. ) 8,1 9,4 11,3 6,9 9,7

Определить: коэффициент корреляции между числом проданных накануне билетов и числом зрителей и построить прямую регрессии.

Примем число билетов за X, а число зрителей за Y. В таблице даны пять реализаций пары случайных величин – пары чисел i=1,,5. Для расчета коэффициента корреляции(rxy) используются следующие формулы:

Эти суммы подставим в формулы (3. 1)-(3. 4). Имеем:

Таким образом, коэффициент корреляции r оказался довольно близким к единице. Для прогнозирования числа зрителей надо найти прямую регрессии Y на X. Подставим найденные значения в формулы (2. 3).

Таким образом, прямая регрессии имеет уравнение и графически изображается на рис. 3. 2.

При измерении в баллах результатов тестирования по математике (X) и физике (Y) получены следующие пары чисел для четырех школьников: (2,2), (4,5), (6,7), (8,10).

Найти : коэффициент корреляции и прямую регрессии Y на X.

Найдем коэффициент корреляции, используя формулы (3. 1)-(3. 4).

Сначала найдем суммы:

Эти суммы подставим в формулы (3. 1)-(3. 4). Имеем:

Таким образом, коэффициент корреляции r оказался довольно близким к единице. Найдем прямую регрессии Y на X. Подставим найденные значения в формулы (2. 3).

Таким образом, прямая регрессии имеет уравнение и графически изображается на рис. 3. 4.

Проводится исследование спроса на некоторый вид товара. Пробные продажи показали следующие данные о зависимости дневного спроса от цены:

Цена, руб. 10 12 14 16 18

Спрос, ед. товара 91 76 68 59 53

Требуется : коэффициент корреляции между ценой X и спросом Y, построить прямую регрессии Y на X.

Найдем коэффициент корреляции, используя формулы (3. 1)-(3. 4).

Сначала найдем суммы:

Эти суммы подставим в формулы (3. 1)-(3. 4). Имеем:

Таким образом, коэффициент корреляции r оказался довольно близким к единице. Найдем прямую регрессии Y на X. Подставим найденные значения в формулы (2. 3).

Математическая обработка экспериментальных данных является важной составляющей многих научных и производственных процессов. С её помощью можно значительно упростить процедуру исследования каких-либо явлений или событий. Допустим, довольно дорогой эксперимент не нужно будет проводить несколько раз, так как его результаты можно будет прогнозировать, исходя из выводов, сделанных на основе раннее проделанного опыта. Поэтому значимость обработки экспериментальных данных приобретает всё более масштабный характер.

Тема работы “Математическая обработка опытных данных” широко применима в различных науках, где целью познания является эксперимент, а он в свою очередь нуждается в математической обработке, например, в физике, экономике, химии, геологии и других. Отсюда вытекает большое значение в теоретическом и практическом применении такого рода знаний в научном и техническом аспектах современной жизни.

Для написания теоретической части работы автором был изучен ряд первоисточников, что позволило привести во второй главе примеры самостоятельного решения пяти задач на применение описанных методов. Поскольку для решения подобных задач требуется решение с большим количеством громоздких вычислительных операций, мною была предпринята попытка облегчить этот процедуру. В приложении представлена программа, написанная на языке программирования Turbo Pascal, для решения задач методом наименьших квадратов, как наиболее часто используемого и точного метода для обработки экспериментальных данных.

Источник

Математическая обработка экспериментальных данных

Математические методы представляют совокуп­ность алгоритмов, основанных на теоретических поло­жениях и идеях определенного раздела математики и позволяющих осуществить комплексный анализ тех или иных закономерностей и отношений. Применение математических методов в инженерной психологии развивается, как уже отмечалось, по трем основным направлениям:

■ математическая обработка экспериментальных данных;

■ математическое моделирование деятельности оператора;

■ вычисление количественных значений инженерно-пси­хологических показателей.

Во многих случаях основным способом вычисле­ния последних является обработка экспериментальных данных или моделирование, поэтому это направление в данном разделе специально не рассматривается. Способы вычисления этих показателей рассматрива­ются при изучении соответствующих вопросов. При­менение математических методов связано с прогрес­сом вычислительной техники, применением ЭВМ в инженерно-психологических исследованиях. Эта связь наиболее ярко проявляется при автоматизации обра­ботки результатов эксперимента, применении имита­ционных моделей деятельности оператора, производ­стве различного рода вычислений.

Основными задачами математической обработки экспериментальных данных являются: определение характеристик случайных величин и событий, сравне­ние между собой их вычисленных значений, построе­ние законов распределения случайных величин, уста­новление зависимости между полученными случайными величинами, анализ случайных процессов. Эти вопро­сы подробно излагаются в специальной литературе [112, 128, 177]. Здесь же представляется целесообразным рас­смотреть лишь особенности и возможности применения их при решении инженерно-психологических задач.

Основными характеристиками случайных величин являются их математическое ожидание и дисперсия, а случайных событий — вероятность их наступления. Математическое ожидание характеризует среднее зна­чение наблюдаемой случайной величины (например, времени реакции, погрешности измерений, числа оши­бок, допущенных человеком при выполнении работы и т. п.), а дисперсия является мерой рассеивания ее зна­чений относительно среднего значения. Выборочные (опытные) значения математического ожидания и дис­персии вычисляются соответственно по формулам

(8.1)

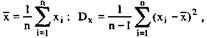
где х_i — наблюденное значение случайной величины,

n — объем выборки (число наблюдений).

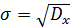
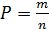
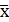
Квадратный корень из дисперсии, т. е. величина, , носит название среднеквадратического отклонения и имеет ту же размерность, что и сама случайная величина. Для оценки вероятности случайного события используют величину , где m — число опытов, в которых данное событие имело место. Чем больше n, тем ближе вычисленные значения , Dx, P к своим истинным значениям, характеризующим генеральную совокупность изучаемой случайной величины.

Сравнение между собой одноименных характери­стик нескольких выборок проводится потому, что в силу ограниченного объема выборки полученные различия между характеристиками случайных величин (матема­тическими ожиданиями, дисперсиями и др.) может быть случайным и не всегда означает, что эти величины различны на самом деле. Проверку этого факта, т. е. проверку статистических гипотез, нужно проводить с помощью непараметрических и параметрических кри­териев согласия.

В первом случае используются не сами значения наблюдаемых величин, а только их упорядоченность (для каждой пары сравниваемых величин известно, какая из них больше), т. е. критерии, не зависящие от параметров распределения. Такие критерии весьма удобны для практического использования, так как тре­буют минимального объема вычислений и априорных сведений и могут использоваться даже при невозмож­ности прямых измерений изучаемых признаков. Такие случаи встречаются, например, при проверке степени различия индивидуальных качеств двух групп опера­торов в случае, если эти качества не могут быть коли­чественно определены. Основными из непараметри­ческих критериев согласия являются критерий знаков, критерий Смирнова и критерий Вилконсона.

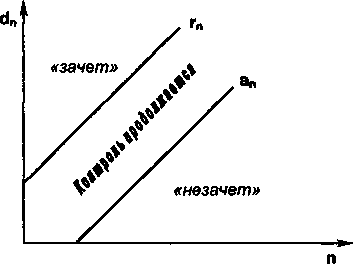
Одним из способов проверки статистических ги­потез является последовательный анализ. Он приме­няется в том случае, когда число наблюдений в ис­следовании не устанавливается заранее, а является случайной величиной. Особенность последовательно­го анализа состоит в том, что после осуществления каж­дого наблюдения принимается одно из следующих решений: принять проверяемую гипотезу, отвергнуть ее, продолжать испытания. Прикладные задачи иссле­дования, в которых применяется последовательный анализ, могут быть теми же, что и в случае проверки гипотез по выборкам заданной длины, но при этом возможна существенная экономия в длительности эк­сперимента. В инженерной психологии последователь­ный анализ широко используется, например, при оцен­ке результатов деятельности оператора. С его помощью определяется то число опытов (решаемых оператором учебных задач), по выполнении которых оператору с заданной достоверностью выставляется оценка «зачет» или «незачет».

Процедура последовательного анализа сводится к следующему. На каждом шаге испытаний после каж­дого опыта фиксируется число d_n благоприятных исхо­дов среди проведенных п наблюдений. По известным формулам [15], зная заданные вероятности ошибок первого и второго рода, определяются значения оце­ночных границ а_n и r_n. В системе координат (d_n, n) стро­ятся две параллельные прямые г_п (п) и а_п (п), имеющие одинаковый угловой коэффициент (рис. 8.1). Точки (d_n, n) наносятся на график по ходу контроля, и эксперимент проводится до тех пор, пока очередная точка не вый­дет за пределы полосы, заключенной между прямыми а_п и г_п. Если d_nn, то оператор получает «незачет», если

Рис. 8.1. Схема проведения последовательного анализа

d_n>r_n— «зачет». В случае, если a_n 2 или Колмо­горова. При этом следует иметь в виду, что одно и то же опытное распределение может дать положительный результат при сравнении не с одним, а с несколькими теоретическими распределениями. Такое обстоятель­ство имеет место, например, при изучении времени реакции оператора [182]. В таких случаях следует опи­раться не только на результаты формальной проверки с помощью критериев согласия, а изучать прежде все­го психологическую сущность и условия применимос­ти того или иного закона распределения.

Для определения связи между двумя и более пере­менными используются такие методы статистического анализа, как корреляционный, регрессионный, диспер­сионный, факторный и др. Корреляционный анализ служит для установления вида, знака и тесноты связи между двумя или несколькими случайными переменны­ми. В первом случае используют коэффициент парной корреляции, во втором — коэффициент множественной корреляции. Примером использования корреляционно­го анализа в инженерной психологии является, в част­ности, проверка прогностической валидности психоди- агностических тестов. Мерой валидности является в этом случае коэффициент корреляции оценок испы­туемых по психофизиологическим методикам с оцен­ками их профессиональной деятельности (т. е. с вне­шним критерием). Однако всегда следует помнить, что при интерпретации результатов корреляционного анализа необходима особая осторожность при учете статистически достоверных высоких корреляций: иногда могут возникнуть ложные корреляции за счет того, что обе изучаемые переменные испытывают сильное влияние третьего, не учтенного при наблю­дении фактора.

Для более углубленного изучения сопряженности количественных показателей в исследуемой совокуп­ности объектов служит регрессионный анализ. Регрес­сия (от лат. regressio — движение назад), выражаемая либо графически, либо аналитически, показывает как в среднем изменяется изучаемый показатель при из­менениях какого-то фактора (факториального показа­теля). Так же как и корреляция, регрессия может быть парной, либо множественной. В общем случае проце­дура регрессивного анализа (на примере парной рег­рессии) сводится к следующему. Пусть есть основания полагать, что изучаемые случайные величины х и у связаны некоторым соотношением. Тогда задача его описания распадается на установление общего вида зависимости и вычисление оценок его параметров. Стандартных методов выбора общего вида кривой не существует: здесь необходимо сочетать визуальный анализ корреляционного поля с качественным анали­зом природы переменных. Методы оценки параметров наиболее хорошо разработаны для линейных зависи­мостей, основным из них является метод наименьших квадратов. В общем виде уравнение множественной линейной регрессии имеет вид

(8.2)

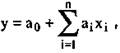
где а₀ и а_i — неизвестные коэффициенты, определяе­мые методом наименьших квадратов; x_i — исследуемые психологические показатели; n — число учитываемых показателей.

При п = 1 выражение (8.2) превращается в уравне­ние парной регрессии. Выражения типа (8.2) называ­ются также регрессионными моделями. В заключение отметим, что регрессия показывает лишь как изменя­ется изучаемый показатель в зависимости от измене­ния факторных показателей, но она ни в коем случае не показывает причинно-следственных связей между показателями.

При изучении трудовой деятельности часто при­ходится оценивать достоверность и степень влияния какого-либо фактора (или факторов) на изменение ве­личины некоторого показателя деятельности человека по сравнению со случайными причинами (например, случайным изменением значений изучаемого показа­теля от опыта к опыту). Эффективным методом реше­ния подобных задач является дисперсионный анализ. В зависимости от числа факторов, влияние которых исследуется, дисперсионный анализ подразделяется на одно-, двух-, трех- и т. д. факторный. При проведении дисперсионного анализа вся совокупность эксперимен­тальных данных разбивается на группы по градациям факторов. Градации могут различаться либо качествен­но, либо количественно по степени действия фактора. Так, при изучении влияния космического полета на психофизиологические показатели космонавта в дис­персионный комплекс были включены такие факторы, как условия работы космонавта с двумя градациями (полетные условия, земные условия); индивидуальность космонавта, каждую градацию которой представлял конкретный человек [137]. Значимость влияния факто­ра оценивается с помощью критерия согласия Фише­ра, представляющего в данном случае отношение факториальной (межгрупповой) дисперсии к случайной (внутригрупповой). Если различие между этими дис­персиями оказывается значимым, то и действие фак­тора на исследуемый показатель деятельности челове­ка оказывает существенное влияние.

Для исследования статистически связанных при­знаков с целью установления определенного числа скрытых от наблюдения факторов используют фактор­ный анализ. С его помощью устанавливается связь изменения одной переменной (например, показателя деятельности оператора) с изменением другой переменной и определяются основные факторы, лежащие в основе указанных изменений. Несколько реже по сравнению с рассмотренными при математической обработке данных в инженерной психологии исполь­зуются латентный и кластерный анализы.

Многие из изучаемых в инженерной психологии процессов носят вероятностный характер и поэтому описываются случайными функциями. Примером их является большинство электрофизиологических пока­зателей, рассмотренных в главе VII: ЭЭГ, ЭКГ, ЭМГ, ЭОГ и др. Математическая обработка эксперименталь­ных данных заключается в этом случае в вычислении основных характеристик данной случайной функции по ее отдельным реализациям, зарегистрированным в ходе эксперимента. Важной задачей при этом является установление таких свойств случайного процесса, как стационарность (постоянство основных характеристик во времени) и эргодичность (совпадение математичес­ких ожиданий и других характеристик для всех имею­щихся реализаций данной случайной функции). Для анализа стационарных процессов применяется спект­ральный анализ. Свойство эргодичности позволяет выявить все характеристики данной случайной функ­ции по одной достаточно длинной реализации, в то время как характеристики не эргодических процессов возможно определить лишь при достаточно большом числе реализаций.

В инженерной психологии, как правило, экспери­ментальному изучению подвергается не вся генераль­ная совокупность, а только часть ее — выборка; т. е. группа испытуемых, представляющих определенную популяцию и отобранных для эксперимента или на­блюдения. На основании полученных характеристик выборки делаются выводы о генеральной совокупно­сти. Практически любое статистическое исследование в инженерной психологии основано на анализе свойств и характеристик определенной выборки. Ее объем определяется двумя противоречивыми услови­ями. С одной стороны, она должна быть достаточно большой, чтобы правильно отразить все свойства ге­неральной совокупности. С другой стороны, она не должна быть чрезмерно большой, чтобы была реаль­ная возможность ее изучения. Поэтому результаты математической обработки экспериментальных дан­ных для выборки (вследствие случайного отбора в нее объектов из генеральной совокупности) могут отли­чаться от соответствующих характеристик генераль­ной совокупности. В связи с этим необходимо оценить достоверность полученных результатов, т. е. возмож­ность их распределения на всю генеральную совокуп­ность.

Для оценки достоверности пользуются принципом практической уверенности. Он состоит в том, что до­стоверным считают событие, имеющее достаточно большую, близкую к единице, вероятность. Такая ве­роятность называется доверительной. Величина, до­полняющая ее до единицы, называется уровнем зна­чимости. Он представляет собой вероятность того, что заключение, принятое достоверным, на самом деле окажется ошибочным. Общепринятыми считаются три уровня значимости: 0,05 —- для обычных исследо­ваний, 0,01 — для важных исследований, 0,001 — для особо важных исследований (например, связанных с отсутствием вредности какого-либо воздействия на человека). Соответствующие этим уровням значимо­сти доверительные вероятности соответственно рав­ны: 0,95; 0,99; 0,999. При построении законов распре­деления случайных величин вычисляется также для заданной доверительной вероятности диапазон воз­можных значений генеральной статистической ха­рактеристики. Этот диапазон называется доверитель­ным интервалом.

При отборе данных, характеризующих ту или иную выборку в инженерно-психологических исследованиях, следует учитывать в ряде случаев различные проявле­ния изменчивости характеристик оператора. Существу­ет по крайней мере два ее проявления. Во-первых, от индивидуума к индивидууму (индивидуальные разли­чия между операторами); во-вторых, для конкретного индивидуума — случайное изменение характеристик оператора от опыта к опыту. Одновременный учет обоих проявлений изменчивости может проводиться различными способами:

■ при формировании выборки для каждого из п испыту­емых берется по некоторому числу m реализаций слу­чайной величины, всего получается N = m-n значений;

■ с помощью жребия выбирается конкретный оператор и для него берется требуемое число значений изучаемой случайной величины;

■ выборка формируется по всем п операторам из сред­них значений изучаемой случайной величины, получен­ных на основании усреднения m значений этой величи­ны для каждого оператора, что эквивалентно, как и в первом случае, общему объему выборки, равному N=mn.

Однако в любом случае выборка обязательно дол­жна быть представительной, т. е. такой, чтобы элемент генеральной совокупности мог попасть в нее с задан­ной вероятностью, не зависящей от характеристик, подлежащих измерению. Такая выборка называется репрезентативной (от фр. representatif — представи­тельный).

Источник