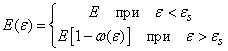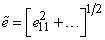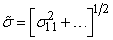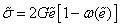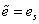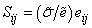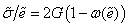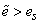какие материалы называются пластичными

Пластичность (физика)

У пластичных материалов прочностные характеристики на растяжение и сжатие сопоставляют по пределу текучести. Принято считать, что σт.р≈σт.с.

Деление материалов на пластичные и хрупкие является условным не только потому, что между теми и другими не существует резкого перехода в значениях δ и ψ. В зависимости от условий испытания многие хрупкие материалы способны вести себя как пластичные, а пластичные — как хрупкие.

Очень большое влияние на проявление свойств пластичности и хрупкости оказывают скорость натяжения и температура. При быстром натяжении более резко проявляется свойство хрупкости, а при медленном — свойство пластичности. Например, хрупкое стекло способно при длительном воздействии нагрузки при нормальной температуре получать остаточные деформации. Пластичные же материалы, такие как малоуглеродистая сталь, под воздействием резкой ударной нагрузки проявляют хрупкие свойства.

Связанные понятия

Упоминания в литературе

Связанные понятия (продолжение)

Термической (или тепловой) обработкой называется совокупность операций нагрева, выдержки и охлаждения твёрдых металлических сплавов с целью получения заданных свойств за счёт изменения внутреннего строения и структуры. Тепловая обработка используется либо в качестве промежуточной операции для улучшения обрабатываемости давлением, резанием, либо как окончательная операция технологического процесса, обеспечивающая заданный уровень свойств изделия.

Диагра́мма фа́зового равнове́сия (диаграмма состоя́ния) желе́зо—углеро́д (иногда эту диаграмму называют «диаграмма железо—цементит») — графическое отображение фазового состояния сплавов железа с углеродом в зависимости от их химического состава и температуры.

Твёрдые растворы — фазы переменного состава, в которых атомы различных элементов расположены в общей кристаллической решётке.

Источник

Пластичность, в чем она состоит, свойства, примеры, эксперименты

тягучесть это технологическое свойство материалов, позволяющее им деформироваться до растяжения; то есть разделение его двух концов без раннего перелома где-то посередине удлиненного участка. По мере удлинения материала его поперечное сечение уменьшается, становясь более тонким.

Поэтому пластичные материалы механически обрабатывают, чтобы придать им нитевидные формы (провода, кабели, иглы и т. Д.). На швейных машинах катушки с витыми нитями представляют собой домашний пример пластичных материалов; в противном случае текстильные волокна никогда бы не приобрели характерных форм.

Какова цель пластичности в материалах? Способность преодолевать большие расстояния или привлекательные дизайны, будь то для разработки инструментов, украшений, игрушек; или для транспортировки некоторой жидкости, такой как электрический ток.

Последнее приложение представляет собой ключевой пример пластичности материалов, особенно металлов. Тонкие медные провода (верхнее изображение) являются хорошими проводниками электричества, и наряду с золотом и платиной доступны во многих электронных устройствах для обеспечения их работы..

Некоторые волокна настолько тонкие (толщиной всего в несколько микрометров), что поэтическая фраза «золотые волосы» приобретает все истинное значение. То же самое касается меди и серебра.

Пластичность не была бы возможным свойством, если бы не было молекулярной или атомной перегруппировки для противодействия падающей растягивающей силе. И если бы его не существовало, человек никогда бы не узнал о кабелях, антеннах, мостах, которые исчезли бы, и мир остался бы в темноте без электрического света (помимо других неисчислимых последствий).

Что такое пластичность?

В отличие от пластичности пластичность заслуживает более эффективной структурной перестройки.

Почему? Потому что, когда поверхность, где натяжение больше, твердое тело имеет больше средств для скольжения своих молекул или атомов, образуя листы или пластины; в то время как когда напряжение сосредоточено во все меньшем поперечном сечении, молекулярное скольжение должно быть более эффективным для противодействия этой силе..

Не все твердые вещества или материалы могут это сделать, и по этой причине они разрушаются при испытаниях на растяжение. Полученные разрывы в среднем горизонтальны, в то время как из пластичных материалов конические или заостренные, признак растяжения.

Пластичные материалы также могут прорваться через точку напряжения. Это может быть увеличено, если температура повышается, так как тепло способствует и облегчает молекулярные слайды (хотя есть несколько исключений). Именно благодаря этим оползням материал может проявлять пластичность и, следовательно, быть пластичным.

Однако пластичность материала включает в себя другие переменные, такие как влажность, тепло, примеси и способ применения силы. Например, свежеплавленное стекло является пластичным, принимая нитевидные формы; но при охлаждении становится хрупким и может сломаться при любом механическом воздействии.

свойства

Пластичные материалы имеют свои собственные свойства, непосредственно связанные с их молекулярным расположением. В этом смысле жесткий металлический стержень и мокрый глиняный стержень могут быть пластичными, даже если их свойства сильно отличаются.

Тем не менее, все они имеют что-то общее: пластичное поведение до распада. В чем разница между пластиком и упругим предметом?

Эластичный объект обратимо деформируется, что происходит первоначально с пластичными материалами; но сила растяжения увеличивается, деформация становится необратимой, и объект становится пластичным.

С этого момента проволока или нить принимают определенную форму. После непрерывного растяжения его поперечное сечение становится настолько малым, а растягивающее напряжение слишком высоким, так что его молекулярные скольжения больше не могут противодействовать растяжению и в конечном итоге разрушаются..

Если пластичность материала чрезвычайно высока, как в случае с золотом, с помощью одного грамма можно получить провода длиной до 66 км, толщиной 1 мкм..

Чем длиннее проволока, полученная из массы, тем меньше ее поперечное сечение (если у вас нет тонны золота, чтобы построить проволоку значительной толщины)..

Примеры пластичных металлов

Металлы относятся к пластичным материалам с неисчислимым количеством применений. Триада состоит из металлов: золота, меди и платины. Один золотой, другой розовато-оранжевый, а последний серебряный. В дополнение к этим металлам есть и другие с более низкой пластичностью:

-Латунь (и другие металлические сплавы)

-Сталь (хотя на ее пластичность может повлиять, в зависимости от ее углеродного состава и других добавок)

-Свинец (но в определенных небольших температурных диапазонах)

Без предварительных экспериментальных знаний трудно определить, какие металлы действительно пластичны. Его пластичность зависит от степени чистоты и от того, как добавки взаимодействуют с металлическим стеклом.

Другие переменные, такие как размер кристаллических зерен и расположение кристалла, также рассматриваются. Кроме того, количество электронов и молекулярных орбиталей, участвующих в связи металла, то есть в «море электронов», также играет важную роль.

Взаимодействия между всеми этими микроскопическими и электронными переменными делают пластичность концепцией, которую необходимо глубоко проанализировать с помощью многомерного анализа; и вы найдете отсутствие стандартного правила для всех металлов.

Именно по этой причине два металла, хотя и с очень похожими характеристиками, могут быть или не быть пластичными.

Размер зерен и кристаллические структуры металлов

Зерна представляют собой кристаллические участки, которые не имеют заметных неровностей (зазоров) в своих трехмерных решетках. В идеале они должны быть полностью симметричными, а их структура должна быть четко определена..

Каждое зерно для одного и того же металла имеет одинаковую кристаллическую структуру; то есть металл с компактной гексагональной структурой, ГПУ, имеет зерна с кристаллами с системой ГПУ. Они расположены таким образом, что перед силой тяги или растяжения они скользят друг над другом, как если бы они были плоскостями, состоящими из мрамора..

Обычно, когда плоскости, состоящие из мелких зерен, скользят, они должны преодолевать большую силу трения; в то время как если они большие, они могут двигаться более свободно. Фактически, некоторые исследователи стремятся изменить пластичность некоторых сплавов посредством контролируемого роста их кристаллических зерен..

С другой стороны, что касается кристаллической структуры, то обычно металлы с кристаллической системой ГЦК (гранец по центру, или кубические по центру лица) являются наиболее пластичными. Между тем, металлы с ОЦК кристаллической структурой (кубическое тело, кубические с центром на гранях) или ГПУ, как правило, менее пластичны.

Например, и медь, и железо кристаллизуются с помощью ГЦК-компоновки и являются более пластичными, чем цинк и кобальт, оба с ГЦП-компоновками.

Влияние температуры на пластичность металлов

Высокая температура может уменьшить или увеличить пластичность материалов, и исключения также относятся к металлам. Однако, как правило, при размягчении металлов, тем больше возможностей превратить их в нити, не разрывая их..

Это связано с тем, что повышение температуры вызывает колебание металлических атомов, что приводит к объединению зерен; то есть несколько мелких зерен соединяются, образуя крупное зерно.

С более крупными зернами пластичность увеличивается, и молекулярные слайды сталкиваются с меньшим количеством физических препятствий.

Эксперимент по объяснению пластичности у детей и подростков

Пластичность становится чрезвычайно сложной концепцией, если начать анализировать под микроскопом. Итак, как вы объясните это детям и подросткам? Таким образом, что это кажется настолько простым, насколько это возможно, на ваших любопытных глазах.

Жевательная резинка и пластилин

До сих пор мы говорили о металлах и расплавленном стекле, но есть и другие невероятно пластичные материалы: жевательная резинка и пластилин..

Чтобы продемонстрировать пластичность жевательной резинки, достаточно схватить две массы и начать их растягивать; один слева, а другой справа. Результатом будет мост подвески жевательной резинки, который не сможет вернуться к своей первоначальной форме, если не будет разминать руками.

Тем не менее, наступит момент, когда мост в конечном итоге сломается (и пол будет испачкан жвачкой).

На изображении выше показано, как ребенок, нажимающий на контейнер с отверстиями, заставляет пластилин появляться, как если бы это были волосы. Сухое игровое тесто менее пластично, чем маслянистое; следовательно, эксперимент может состоять просто в создании двух дождевых червей: один с сухим пластилином, а другой увлажненный маслом.

Ребенок заметит, что маслянистый червь легче вылепить и набрать длину за счет своей толщины; Пока червь высыхает, он может несколько раз сломаться.

Пластилин также представляет собой идеальный материал, чтобы объяснить разницу между податливостью (лодка, ворота) и пластичностью (волосы, дождевые черви, змеи, саламандры и т. Д.).

Демонстрация с металлами

Хотя подростки не будут манипулировать чем-либо, возможность стать свидетелем образования медных проводов в первом ряду может стать для них привлекательным и интересным опытом. Демонстрация пластичности будет еще более полной, если мы перейдем к другим металлам и, таким образом, сможем сравнить их пластичность..

Далее все провода должны подвергаться постоянному растяжению до их точки разрыва. При этом подросток будет визуально подтверждать, как пластичность влияет на сопротивление проволоки разрыву..

Источник

ПЛАСТИЧНОСТЬ

ПЛАСТИЧНОСТЬ – свойство твердых тел изменять форму и размеры под влиянием внешних нагрузок и сохранять ее, когда нагрузки перестают действовать (после снятия нагрузок).

Первое представление о свойстве материала, называемом пластичностью, дает комок пластилина, который под давлением пальцев легко меняет форму, и сохраняет новую форму после действия на него (в отличие о растянутой пружинки, которая опять сожмется, если ее отпустить В этом смысле говорят, что пружинка упруга, а пластилин пластичен. Пластилин и пластичность – слова одного корня, от греческого слова пластика, что значит лепка, от глагола «лепить» (из глины).

Чтобы получить более точное представление о свойстве пластичности, можно сделать (или представить себе) простой опыт. Пусть есть вытянутый параллелепипед (стержень) из пластилина, длинное ребро которого составляет приблизительно 10 см, а малая грань представляет собой квадрат 1 см × 1 см. Пусть этот стержень опирается концами на две опоры («мостик»). Если на средину стержня класть металлические грузики (например, монеты), то пока нагрузка невелика, изменение формы стержня на глаз незаметно. При дальнейшем нагружении обнаруживается, что в некоторый момент стержень прогибается и становится криволинейным. Если убрать все грузики, криволинейная форма все равно сохранится.

Этот опыт показывает, что стержень из материала, обладающего свойством пластичности, сопротивляется действию нагрузок, почти не изменяя свою форму, до тех пор, пока нагрузка не превысит некоторый порог, после чего происходит заметное изменение формы, сохраняющееся и после снятия нагрузки. В этом суть пластичности, но не вся – изменение формы (деформирование) зависит только от приложенной нагрузки и не изменяется само по себе с течением времени. Если деформирование при неизменной нагрузке все же происходит, то материал называют не пластическим, а вязкопластическим или вязкоупругим (см. РЕОЛОГИЯ; ПОЛЗУЧЕСТЬ). Конечно, пластилин – это знакомый и наглядный пример пластического материала. Важно то, что свойство пластичности присуще очень многим конструкционным материалам. В первую очередь, это – металлы и сплавы – сталь, железо, медь, алюминий и другие, но представление о пластическом деформировании оказывается очень полезным и для понимания процессов деформирования композиционных материалов, в том числе металлокерамических, углеродных и полимерных.

Пластичность материала как бы противопоставлена упругости: пластическое тело сохраняет приданную ему форму, а упругое – восстанавливает первоначальную. Но пластичность противопоставляется еще и хрупкости: пластическое тело отвечает на увеличение нагрузки заметным изменением формы, а хрупкое (например, стекло) – появлением трещин и разрушением.

Изучение пластичности развивается по двум направлениям: одно из них связано, в первую очередь, с проблемами техники и цель его – ответ на вопрос: если конструкция подвергается воздействию внешних сил известной величины, каково при этом меняется форма – т.е. как она деформируется? Это важно знать конструктору, но есть и еще одно важное обстоятельство: обычно пластичность предшествует разрушению, так что изучение пластических деформаций является основой прогноза прочности и долговечности конструкции.

Второе направление изучения пластичности – это исследование того, что происходит в материале, как говорят, на микроуровне, т.е., что происходит внутри материала, например, при пластическом изгибе балки. Можно, по аналогии с опытом на изгиб стержня, сделать опыт на его растяжение: верхний конец стержня (его обычно называют образцом) закрепляют, а к нижнему прикладывают нагрузку. В этом случае заметить на глаз изменение длины образца трудно, но если измерять деформации специальными приборами, то обнаруживается, что процесс деформирования оказывается похожим на тот, что и в опыте с изгибом: при постепенном возрастании растягивающей нагрузки сначала проявляются очень малые упругие деформации, когда же нагрузка достигает порогового значения, то деформации (теперь уже, в основном, пластические) становятся, во-первых, более существенными, а, во-вторых, необратимыми (т.е. не исчезают после снятия нагрузки).

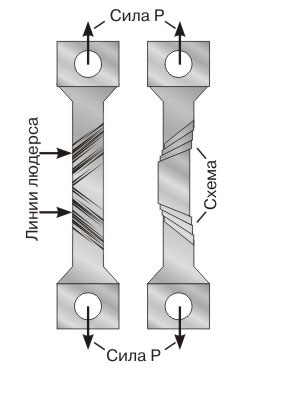
При этом обнаруживаются интересные явления. Если в опыте на растяжение использовать стальной образец в виде длинной пластинки с полированной (зеркальной) поверхностью, то в процессе пластического деформирования на этой поверхности появляется много близких тонких параллельных прямых линий, ориентированных под углом 45° к оси образца (ось образца – здесь прямая линия, проходящая посредине пластинки, параллельно ее длинным сторонам). Эти линии называются линиями Людерса – Чернова (по фамилиям открывших их ученых).

Микроскопический анализ этих линий показывает, что они появляются в результате того, что в материале пластинки происходит сдвиг, т.е. один тонкий слой как бы сдвигается относительно второго, второй – относительно третьего и т.д., как карты в колоде. Можно сказать, что линии Людерса – Чернова и есть границы сдвигающихся слоев. На рис.1 схематически изображена картина такого деформирования. Эта схема позволяет понять, как такие сдвиги приводят к пластическому удлинению образца и почему после снятия нагрузки пластические деформации не исчезают. Более сложные и точные опыты показали, что пластические деформации металлов и сплавов всегда вызываются сдвигами внутри материала. Кроме того, в пористых материалах происходят деформации, по внешним проявлениям очень сходные с пластическими, но связанные с уменьшением пор. Наиболее знакомым пористым материалом является пенопласт; в технике пористые материалы создает порошковая металлургия, где детали прессуются из металлического порошка.

Можно довольно точно описать картину деформирования, считая, что упругие деформации тела – это результат изменения расстояния между атомами, из которых оно состоит, а пластические деформации – результат сдвигов.

Итак, пластичность – результат сдвигов. А как происходят сами сдвиги? На этот вопрос (и на многие другие) отвечают разделы физики: физика твердого тела, теория дислокаций, физика металлов и т.д.

Таковы два направления, по которым исследуется пластичности, первое называется феноменологическим – оно изучает феномен пластичности так, как его можно наблюдать в опытах с образцами и нагрузками, и не опирается на результаты микроскопических опытов. Феноменологическое изучение пластичности металлов начинается с классического опыта на растяжение. Его результаты представляются в виде графиков (рис. 2), где по вертикальной оси откладывается напряжение s, равное растягивающей силе P, отнесенной к площади сечения образца F, т.е.

а по горизонтали – деформация образца e, равная удлинению dl образца (под действием силы P), отнесенному к его первоначальной длине l.

На рис. 2 изображен график, который называется «кривой растяжения»; материал – одна из марок стали. В начале нагружения (на графике от точки O до точки A) напряжение и деформация оказываются пропорциональными, т.е. имеет место закон Гука. Коэффициент пропорциональности называется модулем упругости (или модулем Юнга) E. Точка A на графике называется пределом упругости – после нее пропорциональность, свойственная упругости, сменяется криволинейной зависимостью, причем теперь деформация растет значительно быстрее, чем напряжение. Если в некоторой точке B мы начнем уменьшать напряжение (это называется разгрузкой), то на графике получится кривая, мало отличающаяся от прямой – BC со стрелкой вниз. Если, доведя напряжение до нуля, снова его увеличивать, на графике получится кривая CB1 (со стрелкой вверх), причем далее эта кривая плавно перейдет в кривую B1D, которая получилась бы при деформировании образца без разгрузки. Для простоты обычно обе кривые, BC и CB1, заменяют отрезком прямой B2C, который параллелен отрезку OA.

Есть несколько вариантов теории пластичности, которые отличаются, с одной стороны, тем, насколько точно они учитывают реальные особенности процесса деформирования упруго-пластического материала, и, с другой стороны, используемым математическим аппаратом. Одни теории являются менее точными, но более простыми и удобными для расчетов, что очень важно, так как расчет пластических деформаций в телах сложной формы представляет собой очень трудную задачу даже при использовании современных компьютеров. Другие теории могли бы обеспечить высокую точность, но приводят к очень большим трудностям, как математическим, так и экспериментальным. По-видимому, создание «идеальной» теории, сочетающей физическую наглядность, математическую простоту и в то же время обеспечивающей адекватное описание процессов пластического деформирования, является делом будущего. Но даже «простые» теории пластичности на самом деле достаточно сложны, так как требуют знания и понимания многих экспериментальных результатов и серьезной математической подготовки. В качестве примера можно рассмотреть идею самой простой теории пластичности.

В самом простом случае опыта на растяжение образца процесс упругого деформирования описывается законом Гука

За пределом упругости пропорциональности нет, но экспериментальную кривую растяжения можно описать, если считать, что модуль упругости E при этом перестает быть постоянной величиной и становится функцией деформации, т.е.

В этих формулах появляется новая функция w = w(e), которая называется функцией пластичности и должна быть найдена из экспериментальных данных.

Видно, что функция w(e) тождественно равна нулю при упругих деформациях и возрастает при пластических. Тогда ясно, что и упругие, и пластические деформации описываются уравнением, обобщающим закон Гука

Это уравнение описывает кривую деформирования, из которой оно, по существу, и получено и это так, пока речь идет только об опыте на растяжение. Но теория пластичности должна «уметь» описывать любые процессы деформирования – например, и кручение, и изгиб, и их совместное проявление, а для этого формулу необходимо существенно обобщить и сформулировать аналогичные по сути, но неизмеримо более сложные соотношения, которые связывали бы шесть компонент тензора деформаций с шестью компонентами тензора напряжений. Здесь и начинаются сложности.

Классическая деформационная теория называется «теорией малых упругопластических деформаций». Эта теория основана на трех экспериментальных фактах:

1. При различных упругопластических деформациях в каждой точке тела существует универсальная функциональная зависимость между среднеквадратичным значением сдвиговых деформаций и аналогичным среднеквадратичным значением сдвиговых напряжений.

2. При упругопластическом деформировании материала изменение объема всегда происходит упруго.

3. Первые два утверждения справедливы только при условии, что все внешние силы, действующие на тело, возрастают пропорционально друг другу (точнее – пропорционально одному параметру, например, времени). Это так называемое «простое» или «пропорциональное» нагружение.

Чтобы правильно понять эти три утверждения, нужно принять во внимание следующее:

Теория пластичности, как и все эмпирические теории, по своему существу является теорией приближенной. Это означает, что при известных условиях, когда она может описывать физическую реальность («условия применимости»), эмпирическая теория эту реальность описывает с относительно небольшой, но всегда присутствующей погрешностью (проще говоря, с небольшой ошибкой).

Теория пластичности, о которой идет речь, может дать ответ с погрешностью, близкой к 10%. И почти всегда такая погрешность оказывается вполне приемлемой – говорят, что «теория хорошо работает».

Математическая формулировка теории: пусть есть тензор деформации e ij и тензор напряжений sij. Требуется написать формулы (соотношения), которые связывают эти тензоры при малых упругопластических деформациях, подобно тому, как закон Гука связывает их при упругих деформациях.

Учитывая различные закономерности объемного и сдвигового деформирования, можно разделить тензоры на объемную (шаровую) и сдвиговую (девиаторную) части:

Следующий шаг – установление связи сдвиговых напряжений с деформацииями, поскольку пластичность – это сдвиги.

Для девиатора деформаций среднеквадратичный сдвиг в данной точке определяется формулой

Аналогично, среднеквадратичное сдвиговое напряжение определяется:

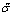
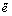
(величины и часто называют «интенсивностями» напряжений и деформаций). Теперь можно математически записать первый постулат:

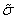
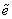
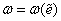
Это и есть универсальная функциональная зависимость между и , а универсальна она в том смысле, что имеет место в любой точке тела и при любом виде деформаций (изгиб, кручение, их комбинация и т.д.). Функция считается известной, а фактически должна быть найдена из обработки результатов эксперимента. Так как в силу универсальности она одинакова всегда, в частности, в любом опыте, то удобно использовать опыт на кручение трубки, из которого эта функция определяется особенно легко.

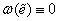
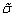
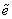
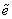
В пределах упругости, и зависимость между и превращается в закон Гука. В теории пластичности считается, что в любой точке тела пластические деформации появляются тогда, когда величина достигает некоторого значения e_s. Это значение находится из эксперимента и называется пределом текучести по деформациям. Таким образом, условие появления первых пластических деформаций запишется в виде

Это условие называется условием пластичности Хубера – Мизеса. Таким образом, можно окончательно записать

Второй постулат записывается в виде: s = KQ

где s – среднее нормальное напряжение (давление) в данной точке, а Q – относительное изменение объема малой частицы, окружающей эту точку. Число K > 0 называется объемным модулем упругости. Таким образом, относительное изменение объема малой частицы пропорционально среднему нормальному напряжению в этой частице.

Теперь можно записать определяющие соотношения теории малых упругопластических деформаций:

Девиаторы напряжений и деформаций связаны пропорциональной зависимостью

Коэффициент пропорциональности за пределами упругости перестает быть постоянным и становится переменной величиной:

Функция 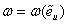становится отличной от нуля при выполнении неравенства, связанного с условиями пластичности Хубера–Мизеса

Шаровые тензоры напряжений деформаций всегда пропорциональны

или, что эквивалентно,

Все это справедливо только при пропорциональном нагружении, которое иногда называют простым, так как сложное нагружение – это непропорциональное нагружение. Оказывается, что в опыте, когда трубка подвергается растяжению силой P и кручению моментом M, деформации будут различными, в зависимости от того, как прикладываются нагрузки: сразу обе, сначала M, потом P, или наоборот. Это обстоятельство приводит к тому, что теорию пластичности при сложном нагружении уже нельзя построить по аналогии с теорией упругости.

Приведенная теория была разработана, экспериментально и теоретически обоснована и внедрена в инженерную практику работами А.Ильюшина, который опирался на работы своих предшественников – в первую очередь, Х.Хенки и Р.фон Мизеса.

Ильюшин А.А., Ленский В.С. Сопротивление материалов, М., Физматгиз, 1959;
Гордон Дж. Почему мы не проваливаемся сквозь пол? М., Изд-во «Мир», 1971;
Безухов Н.И. Основы теории упругости, пластичности и ползучести. М., Изд-во «Высшая школа», 1981

Источник