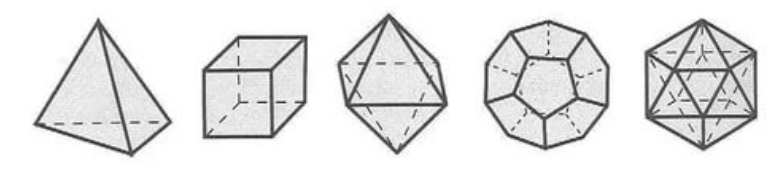
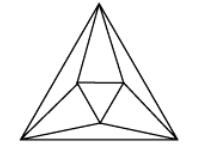
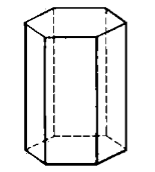
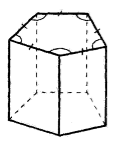
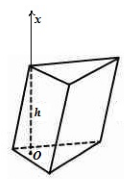
какие многогранники лежат в основании призмы
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Перечень вопросов, рассматриваемых в теме:
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
Рассмотрим два равных многоугольника А1А2. Аn и В1В2. Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С 2 =АА1 2 +АС 2 (1).
Так как в основании прямоугольник, то ВС=АD.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Найдите для каждой картинки пару
1)

4)
6)
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Понятие многогранника. Призма
Вы будете перенаправлены на Автор24
Понятие многогранника
Многогранником называется геометрическое тело в пространстве, которое ограниченно несколькими многоугольниками.
Примеры многогранников Вы можете видеть на рисунке 1.
Рисунок 1. Примеры многогранников
Если многогранник всегда будет лежать по одну сторону от любой плоскости его граней, то многогранник называется выпуклым (рис. 2).
Рисунок 2. Выпуклый многогранник
Рассмотрим далее детально, как пример выпуклого многогранника, призму.
Призма
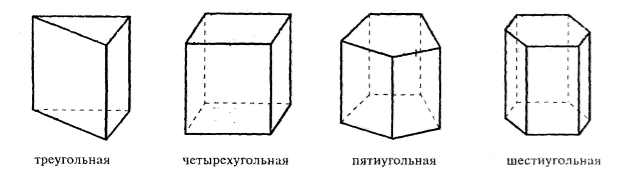
В зависимости от количества углов в основании призмы ее можно назвать треугольной, четырехугольной и так далее (рис. 4).
Готовые работы на аналогичную тему
Отметим, что параллелепипед является частным случаем четырехугольной призмы.
Рисунок 5. Прямая призма
Площадь призмы
Полная площадь призмы определяется следующим образом
Рассмотрим и докажем следующую теорему.
Площадь боковой поверхности прямой призмы определяется как произведение периметра основания данной призмы на ее высоту.
Доказательство.
\[S_<бок>=S_1+S_2+\dots +S_n=a_1h+a_2h+\dots +a_nh=h\left(a_1+a_2+\dots +a_n\right)=P_<осн>h\]
Теорема доказана.
Объем призмы
Объем призмы определяется как произведение площади основания этой призмы на высоту.
Доказательство.
Пример задачи
Решение.
\[S_<осн>=\frac<1><2>\cdot 2\cdot 2\cdot sin<30>^0=2\cdot \frac<1><2>=1\]
По теореме косинуса, третья сторона треугольника равна
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Перечень вопросов, рассматриваемых в теме:
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
Рассмотрим два равных многоугольника А1А2. Аn и В1В2. Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С 2 =АА1 2 +АС 2 (1).
Так как в основании прямоугольник, то ВС=АD.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Найдите для каждой картинки пару
1)

4)
6)
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Призма
Призма
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
В основании лежит четырехугольник
1. Прямоугольник
2. Ромб
3. Трапеция
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Средняя линия треугольника параллельна основанию и равна его половине.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Какие многогранники лежат в основании призмы
Проверяемые элементы содержания и виды деятельности: владение понятиями о стереометрических фигурах; знание их свойств; знание формул для вычисления площадей поверхностей и объемов тел; умение применять эти знания при решении задач.
Ориентировочное время выполнения учащимися: 10—15 минут.
• Элементы, площадь поверхности, объем стереометрических фигур.
Особенности экзаменационных заданий по стереометрии
Задания этого вида представляют собой стереометрические задания на установление взаимосвязи между основными элементами многогранников и круглых тел, а также на использование формул для вычисления их площадей поверхностей и объемов. Вычислительной трудности задания не представляют; решение, как правило, сводится к использованию одной-двух формул. Соответствующие формулы нужно знать наизусть.
Куб — правильный многогранник, каждая грань которого представляет собой квадрат. Куб является частный случаем параллелепипеда и призмы, поэтому для него выполнены все их свойства. Кроме того, если а — длина ребра куба, — диагональ основания,
— диагональ куба,
— площадь полной поверхности, а V — объем куба, то справедливы формулы:
Призма. Прямоугольный параллелепипед
Призмой (n-угольной призмой) называется многогранник, две грани которого — равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней — параллелограммы.
Правильной призмой называется прямая призма, основание которой — правильный многоугольник.
Прямой призмой называется призма, боковое ребро которой перпендикулярно плоскости основания. Высота прямой призмы равна ее боковому ребру, а все боковые грани прямой призмы — прямоугольники.
Соотношения для прямой призмы
Пусть H — высота прямой призмы, AA1 — боковое ребро, — периметр основания,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем прямой призмы. Тогда имеют место следующие соотношения:
Особенности правильной шестиугольной призмы
В основании правильной шестиугольной призмы лежит правильный шестиугольник. Напомним его свойства.
— Сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
— Большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам.
— Меньшая диагональ правильного шестиугольника в раз больше его стороны.
— Угол между сторонами правильного шестиугольника равен 120°.
— Меньшая диагональ правильного шестиугольника перпендикулярна его стороне.
— Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.
Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками
,
и многоугольником
вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).
Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.
Соотношения для правильной пирамиды
Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды,
— площадь основания,
— площадь боковой поверхности,
— площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:
Секущей плоскостью многогранника называется любая плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Тетраэдр имеет четыре грани, поэтому его сечениями могут быть только треугольники и четырехугольники (рис. 1). Параллелепипед имеет шесть граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники (рис. 2).
Теоремы, используемые при построении сечений
Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Поэтому секущая плоскость пересекает плоскости параллельных граней по параллельным прямым.
Теорема 2. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема 3. Если прямая l параллельна какой либо прямой m, проведённой в плоскости то она параллельна и самой плоскости
Теорема 4. Если прямая, лежащая в плоскости сечения, не параллельна плоскости некоторой грани, то она пересекается со своей проекцией на эту грань.
Алгоритм построения сечений
Для построения сечений рекомендуем пользоваться следующим алгоритмом.
1. Если две точки секущей плоскости лежат в плоскости одной грани, то проводим через них прямую. Часть прямой, лежащая в плоскости грани — сторона сечения.
2. Если прямая a является общей прямой секущей плоскости и плоскости какой-либо грани, то находим точки пересечения прямой a с прямыми, содержащими ребра этой грани. Полученные точки — новые точки секущей плоскости, лежащие в плоскостях граней.
3. Если никакие две из данных точек не лежат в плоскости одной грани, то строим вспомогательное сечение, содержащее любые две данные точки, а затем выполняем шаги 1, 2.
Для контроля правильности построенного сечения, проверяйте, что:
— все вершины сечения лежат на рёбрах многогранника;
— все стороны сечения лежат в гранях многогранника;
— в каждой грани многогранника лежит не более одной стороны сечения.
Цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону.
Соотношения для цилиндра
Пусть h — высота цилиндра, r — радиус основания, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем цилиндра. Тогда имеют место следующие соотношения:
Конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет.
Соотношения для конуса
Пусть h — высота конуса, r — радиус основания, l — образующая, Sбок — площадь боковой поверхности, Sполн — площадь полной поверхности, V — объем конуса. Тогда имеют место следующие соотношения:
Сфера и шар
Шаром называется фигура, полученная при вращении полукруга вокруг оси, содержащей его диаметр. Сферой называется поверхность шара. Пусть R — радиус шара, S — площадь сферы, V — объем шара. Тогда имеют место следующие соотношения:
Комбинации круглых тел. Вписанные сферы
Сфера называется вписанной в цилиндр, если она касается обоих оснований цилиндра и каждой его образующей.
Сфера называется вписанной в конус, если она касается основания конуса и каждой его образующей.
Сфера называется вписанной в усечённый конус, если она касается обоих оснований конуса и всех его образующих.
Теорема 1: В прямой круговой цилиндр можно вписать сферу тогда и только тогда, когда его высота равна диаметру основания. Причём центр сферы есть середина оси цилиндра.
Теорема 2: В любой прямой круговой конус можно вписать сферу. Причём центр сферы есть точка пересечения оси конуса с биссектрисой угла наклона образующей конуса к плоскости его основания.
Теорема 3. В усечённый конус можно вписать сферу тогда и только тогда, когда он прямой круговой, и длина его образующей равна сумме длин радиусов оснований. Причём центр сферы есть середина оси усечённого конуса.
Комбинации круглых тел. Описанные сферы
Сфера называется описанной около цилиндра, если окружности его оснований лежат на сфере.
Сфера называется описанной около конуса, если вершина конуса и его основание лежат на сфере.
Теорема 1: около цилиндра можно описать сферу тогда и только тогда, когда он прямой круговой. Причём центр сферы есть середина оси цилиндра.
Теорема 2: около конуса можно описать сферу тогда и только тогда, когда он круговой. Причём центр сферы есть точка пересечения прямой, перпендикулярной к плоскости основания и проходящей через центр его, и плоскости, перпендикулярной какой-либо его образующей конуса и проходящей середину этой образующей.
Следствие: сферу можно описать около любого прямого кругового конуса. В этом случае, центр сферы — точка пересечения прямой, содержащей высоту конуса с плоскостью, перпендикулярной какой-либо из его образующих и проходящей через ее середину.
Комбинации конуса и цилиндра
Цилиндр называется вписанным в конус, если одно его основание лежит на основании конуса, а второе совпадает с сечением конуса плоскостью, параллельной основанию. Конус в этом случае называется описанным вокруг цилиндра.
Цилиндр называется описанным вокруг конуса, если центр одного из оснований цилиндра является вершиной вершина конуса, а противоположное основание цилиндра совпадает с основанием конуса. Конус в этом случае называется вписанным в цилиндр.
Комбинации многогранников и круглых тел. Описанные сферы
Сфера называется описанной около многогранника, если все его вершины лежат на этой сфере. Многогранник называется в этом случае вписанным в сферу.
Возможность описать сферу около многогранника означает существование точки (центра сферы), равноудалённой ото всех вершин многогранника.
Теорема 1: если из центра описанной около многогранника сферы опустить перпендикуляр на какое-либо из его рёбер, то основание этого перпендикуляра разделит ребро на две равные части.
Теорема 2: если из центра описанной около многогранника сферы опустить перпендикуляр на какую-либо из его граней, то основание этого перпендикуляра попадёт в центр круга, описанного около соответствующей грани.
Теорема 3: если около многогранника описана сфера, то её центр лежит на пересечении перпендикуляров к каждой грани пирамиды, проведённых через центр окружности, описанной около соответствующей грани.
Теорема 4: если около многогранника описана сфера, то её центр является точкой пересечений всех плоскостей, проведённых через середины рёбер пирамиды перпендикулярно к этим рёбрам.
Комбинации многогранников и круглых тел. Вписанные сферы
Сфера называется вписанной в многогранник, если все его грани касаются этой сферы. Многогранник называется в этом случае описанным около сферы.
Теорема: если в многогранник с площадью поверхности S и объёмом V вписан шар радиуса r, то справедливо соотношение:
Комбинации конуса, цилиндра и многогранников
В условиях задач встречаются также следующие понятия, не входящие в школьные учебники, которые уточняются непосредственно в условиях задач. Приведем наиболее употребительные из них.
Цилиндр вписан в призму: основания цилиндра вписаны в основания призмы.
Цилиндр описан вокруг призмы: основания цилиндра описаны вокруг оснований призмы.
Цилиндр вписан в пирамиду: одно из основание цилиндра вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание цилиндра принадлежит основанию пирамиды.
Цилиндр описан вокруг пирамиды: вершина пирамиды принадлежит одному из оснований цилиндра, а другое его основание описано вокруг основания пирамиды.
Конус вписан в призму: основание конуса вписано в основание призмы, а вершина конуса принадлежит противоположному основанию призмы.
Конус описан вокруг призмы: одно из оснований призмы вписано в сечение пирамиды плоскостью, параллельной основанию, а другое основание призмы вписано в основание конуса.
Конус вписан в пирамиду: их вершины совпадают, а основание конуса вписано в основание пирамиды. Вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой.
Конус описан вокруг пирамиды: их вершины совпадают, а основание конуса описано вокруг основания пирамиды.