какие многоугольники могут получиться в сечении параллелепипеда
Какие многоугольники могут получиться в сечении тетраэдра, параллелепипеда? Вопрос №16 к 1 главе, Геометрия, 10-11 класс, Атанасян Л.С.
Последний вопрос главы.
Какие многоугольники могут получиться в сечении: а) тетраэдра; б) параллелепипеда?
Ловите!
а) Треугольники и 4-угольники; б) 3-, 4-, 5-, 6-угольники.
Привет. Запуталась при решении, нужна помощь знатоков.
Три прямые, проходящие через одну точку и не лежащие в одной ( Подробнее. )
Виды сечений параллелепипеда
Решение задач на построение сечений
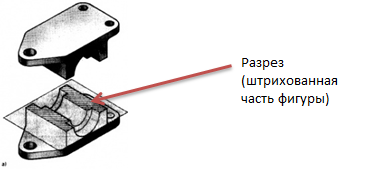
| Подумайте, какой школьный предмет позволяют научиться правильно выполнять и оформлять чертежи, познакомится с различными графическими способами передачи сведений об объектах предметного мира. Правильно! Это черчение. Для изготовления деталей на заводе используются точные чертежи этих деталей в разрезе. Разрезы используются для показа внутренней формы изделия. Разрезом называется изображение, полученное при мысленном рассечении детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости. | На экране изображение  На экране изображение На экране изображение  На экране рисунок На экране рисунок
На экране изображение и текст: Сечение параллелепипеда На экране изображение и текст: Виды сечений параллелепипеда
На экране изображение: На экране обновляется изображение На экране обновляется чертёж | ||||||||||||
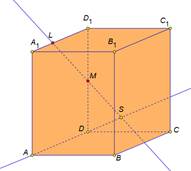
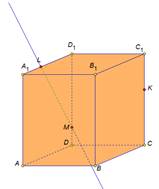
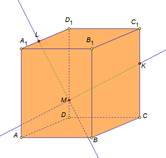
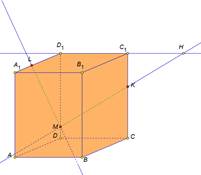
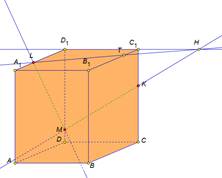
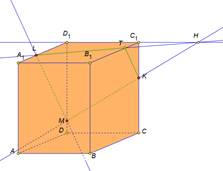
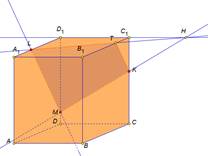
| Рассмотрим задачу на построение сечения параллелепипеда. На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM. Построим данный параллелепипед и отметим указанные точки. Так как точки L и M принадлежат грани АА1D1D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА1D1D секущей плоскостью. Аналогично в грани DD1C1C построим прямую MK и выделим отрезок MK. В грани А1B1C1D1 есть только одна точка L, для построения второй точки продлим до пересечения прямые D1C1 и MK. Отметим их общую точку H. Точка H принадлежит секущей плоскости, так принадлежит прямой MK. И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость. Так как точки T и К принадлежат секущей плоскости и грани ВВ1С1С, то отрезок ТК будет следом от сечения в этой грани. Выделим получившийся четырехугольник KMLT. Это искомое сечение. Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство. Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение. | На экране текст: На рёбрах CC1,A1D1, DD1 параллелепипеда АВСDA1B1C1D1 отмечены точки K,L,M соответственно. Построить сечение параллелепипеда плоскостью KLM. На экране изображение: 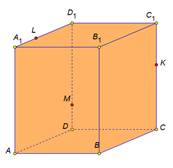 На экране изображение: На экране изображение:
На экране изображение и и текст:
На экране изображение и текст:
На экране изображение и текст:
На экране изображение:
На экране изображение:
Комментарий: задачи разобраны очень подробно, оформлены, четко структурированы. были небольшие опечатки по ходу решения. Построение сечений прямоугольного параллелепипеда (урок геометрии в 10 классе) Описание презентации по отдельным слайдам: Урок геометрии в 10 классе Подготовила учитель математики МБОУ СОШ № 4 г. Михайловска Мишустина Е. В. Какие многоугольники могут получиться в сечении параллелепипеда? Построить сечение плоскостью АВС А В С A B С B1 D1 D K M C1 A1 ВАЖНО! Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам. Построить сечение плоскостью DМК А В С Построить сечение плоскостью АВС Построить сечение плоскостью, проходящей через точку М и параллельно плоскости ВDD1 A B C1 D A1 B1 D1 C M Построить сечение плоскостью АВС В С Построить сечение плоскостью, проходящей через диагональ АС параллельно ВD1 A C1 D A1 B1 D1 B C Построить сечение плоскостью MNK A C1 D A1 B1 D1 B C M N K Построить сечение плоскостью MNK A C1 D A1 B1 D1 B C M N K Построить сечение плоскостью MNK A C1 D A1 B1 D1 B C M N K Домашнее задание № 84, 85 Курс повышения квалификации Дистанционное обучение как современный формат преподаванияКурс повышения квалификации Методика обучения математике в основной и средней школе в условиях реализации ФГОС ООКурс профессиональной переподготовки Математика: теория и методика преподавания в образовательной организацииИщем педагогов в команду «Инфоурок» Номер материала: ДБ-513146 Международная дистанционная олимпиада Осень 2021 Не нашли то что искали? Вам будут интересны эти курсы: Оставьте свой комментарийАвторизуйтесь, чтобы задавать вопросы. Безлимитный доступ к занятиям с онлайн-репетиторамиВыгоднее, чем оплачивать каждое занятие отдельно Российские школьники завоевали пять медалей на олимпиаде по физике Время чтения: 1 минута Руководители управлений образования ДФО пройдут переобучение в Москве Время чтения: 1 минута В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана Время чтения: 1 минута Минпросвещения будет стремиться к унификации школьных учебников в России Время чтения: 1 минута Минпросвещения разрабатывает образовательный минимум для подготовки педагогов Время чтения: 2 минуты Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года Время чтения: 1 минута Подарочные сертификатыОтветственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи. Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов. Геометрия. 10 классКонспект урокаГеометрия, 10 класс Урок №7. Тетраэдр и параллелепипед Перечень вопросов, рассматриваемых в теме Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Сечением поверхности геометрических тел называется – плоская фигура, полученная в результате пересечения тела плоскостью и содержащая точки, принадлежащие как поверхности тела, так и секущей плоскости. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Учебник Геометрия 10-11 кл.– М.: Просвещение, 2014. Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014. Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013. Открытый электронный ресурс: Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru Теоретический материал для самостоятельного изучения В дельнейшем несколько уроков нашего курса будет посвящены многогранникам- поверхностям геометрических тел, составленным из многоугольников. Но до более подробного изучения многогранников мы познакомимся с двумя из них- тетраэдром и параллелепипедом. Нам данные тела дадут возможность проиллюстрировать понятия, связанные со взаимным расположением прямых и плоскостей. Давайте вспомним, что мы понимали под многоугольником в планиметрии. Многоугольник мы рассматривали либо как замкнутую линию без самопересечений, либо как часть плоскости, ограниченную этой линией, включая ее саму. Мы будем использовать второе толкование многоугольника при рассмотрении поверхностей и тел в пространстве. При таком толковании любой многоугольник в пространстве представляет собой плоскую поверхность. Давайте рассмотрим изображенную фигуру и ответим на несколько вопросов. Итак, поверхность данной фигуры состоит из четырёх треугольников DАВ, DВС, DАС и АВС. Мы с вами выяснили из элементов состоит наша фигура тетраэдр. Теперь сформулируем определение. Определение. Тетраэдр – это многогранник, состоящий из плоскости треугольника и точки не лежащий в этой плоскости, трех отрезков соединяющих эту точку с вершинами основания треугольника. Говорят, что рёбра АD и ВС, АВ и CD, и т.д.- противоположные. Изображается тетраэдр обычно так (рис. 1). Рисунок 1 – изображение тетраэдра. Математика, в частности геометрия, является мощнейшим инструментом в познании мира. Различные геометрические формы находят свое практическое приспособление в различных областях знания: архитектуре, скульптуре, живописи. И тетраэдр тому доказательство. Так же мы можем наблюдать тетраэдр в повседневной жизни (рис. 2). Форма пакета молока Прежде чем начать изучать параллелепипед вспомним определение параллелограмма и его свойства. Определение. Четырёхугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом (рис. 3). Рисунок 3 – параллелограмм 1. Противоположные стороны параллелограмма равны: 2. Противоположные углы параллелограмма равны: 3. Диагонали параллелограмма точкой пересечения делятся пополам: треугольники ABC и CDA равны. 6. Накрест лежащие углы при диагонали равны: А теперь перейдем к параллелепипеду. Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, расположенных в параллельных плоскостях так, что отрезки AA1, BB1, CC1 и DD1 параллельны. Давайте рассмотрим изображенную фигуру (рис. 4). Рисунок 4 – параллелепипед и его диагонали АВСDA1B1C1D1: поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1, лежащих в параллельных плоскостях и четырёх параллелограммов. Определение. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: Параллелепипед – слово греческого происхождения, параллел – идущий рядом, епипед – плоскость. Определение.Параллелепипед- этошестигранник с параллельными и равными противоположными гранями. Следует отметить, что многоугольник в пространстве представляет собой плоскую поверхность, а тетраэдр и параллелепипед – поверхности, составленные из плоских поверхностей (соответственно треугольников и параллелограммов). Способы изображения параллелепипеда Параллелепипед, в основании которого лежит ромб Параллелепипед, в основании которого лежит квадрат Параллелепипед,в основании которого лежит прямоугольник или параллелограмм Параллелепипед, у которого все грани — равные квадраты Можно сделать вывод, что параллелепипеды делятся на (рис. 5) Рисунок 5 – виды параллелепипедов В параллелепипеде ABCDA1B1C1D1грани ВВ1С1С и AA1D1D параллельны (рис. 6), потому что две пересекающиеся прямые ВВ1 и В1С1 одной грани параллельны двум пересекающимся прямым АА1 и A1D1 другой; эти грани и равны, так как В1С1 = A1D1, В1В= А1А (как противоположные стороны параллелограммов) и ∟ ВВ1С1= ∟АA1D1. Рисунок 6 – чертеж к доказательству свойства 1 Возьмём какие-нибудь две диагонали, например АС1 и ВD1, и проведём вспомогательные прямые АD1 и ВС1 (рис. 7). Так как рёбра АВ и D1С1 соответственно равны и параллельны ребру DС, то они равны и параллельны между собой; вследствие этого фигура АD1С1В есть параллелограмм, в котором прямые С1А и ВD1 —диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам. Возьмём теперь одну из этих диагоналей, например АС1, с третьей диагональю, положим, с В1D. Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B1D и АС1 и диагонали АС1 и BD1(которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали Рисунок 7 – чертеж к доказательству свойства 2 Задачи на построение сечений. Взаимное расположение многогранника и секущей плоскости: Фигуры, которые получаются в результате сечения: Один из методов построения сечений, который мы рассмотрим- метод следа. Рассмотрим метод следов, применяемый при построении сечений многогранников, а именно при построении сечения куба плоскостью. Что такое метод следов? При построении сечений многогранников в качестве вспомогательной прямой часто используется след секущей плоскости (в плоскости грани, удобной для рассмотрения). Такой метод построения сечений называется методом следа. Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R (рис. 8). Рисунок 8 –чертеж к задаче №1 Основные правила построения сечений методом следа: То есть, суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Дан тетраэдр АВСD. Точка М – точка внутренняя, точка грани тетраэдра АВD. N – внутренняя точка отрезка DС. Построить точку пересечения прямой NM и плоскости АВС. Рисунок 9 – чертеж к задаче №2 Решение: Примеры и разбор решения заданий тренировочного модуля Дан тетраэдр АВСD. М – внутренняя точка грани АВD. Р – внутренняя точка грани АВС. N – внутренняя точка ребра DС. Построить сечение тетраэдра плоскостью, проходящей через точки М, N и Р. Решение: Проведем прямую КР. Прямая КР лежит и в плоскости сечения, и в плоскости АВС. Получаем точки Р1 и Р2. Соединяем Р1 и М и на продолжении получаем точку М1. Соединяем точку Р2 и N. В результате получаем искомое сечение Р1Р2NМ1. Задача в первом случае решена. Рисунок 10 – чертеж к примеру 1 (первый случай) Рассмотрим второй случай, когда прямая MN параллельна плоскости АВС (рис. 12). Плоскость МNР проходит через прямую МN параллельную плоскости АВС и пересекает плоскость АВС по некоторой прямой Р1Р2, тогда прямая Р1Р2 параллельна данной прямой MN. Рисунок 11 – чертеж к примеру 1 (второй случай) Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым. Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N (рис. 13).
|









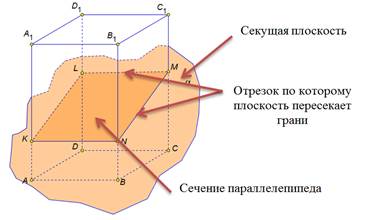
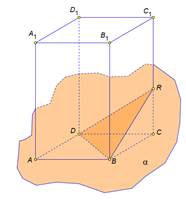 В сечении паралелепипеда плоскостью лежит треугольник
В сечении паралелепипеда плоскостью лежит треугольник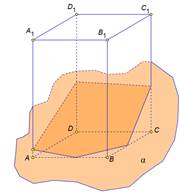 В сечении паралелепипеда плоскостью лежит пятьугольник
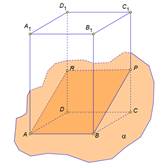
В сечении паралелепипеда плоскостью лежит пятьугольник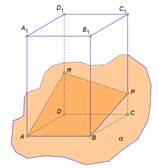
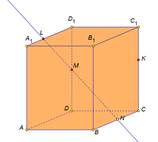

































 следовательно, PM||NQ.Утверждение доказано.
следовательно, PM||NQ.Утверждение доказано.