какие модули имеют противоположные числа
Математика. 6 класс
Конспект урока
Противоположные числа. Модуль числа
Перечень рассматриваемых вопросов:
Числа, которые отличаются только знаком, называются противоположными.
Модулем положительного числа называют само это число.
Модулем отрицательного числа называют противоположное ему (положительное) число.
Модулем числа 0 является число 0.
Теоретический материал для самостоятельного изучения
Считается, что если перед целым числом поставить знак «+», то это не изменяет самого числа.
число 7 можно записать как + 7
число – 7 можно записать как + (– 7)
Поэтому ряд целых чисел можно записывать в виде:
…, – 6, – 5, – 4, – 3, – 2, – 1, 0, + 1, + 2, + 3, + 4, + 5, + 6, …
Числа, которые отличаются только знаком, называются противоположными.
Например, противоположные числа:
Модуль или абсолютная величина числа.
Разбор заданий тренировочного модуля
№2. Ввод с клавиатуры пропущенных элементов в текст.
Числа. Модуль числа.
Модуль положительного действительного числа a – это само это число. Число в модуле:
Модуль отрицательного действительного числа а – это противоположное ему число:
В общем случае запись модуля числа выглядит так:
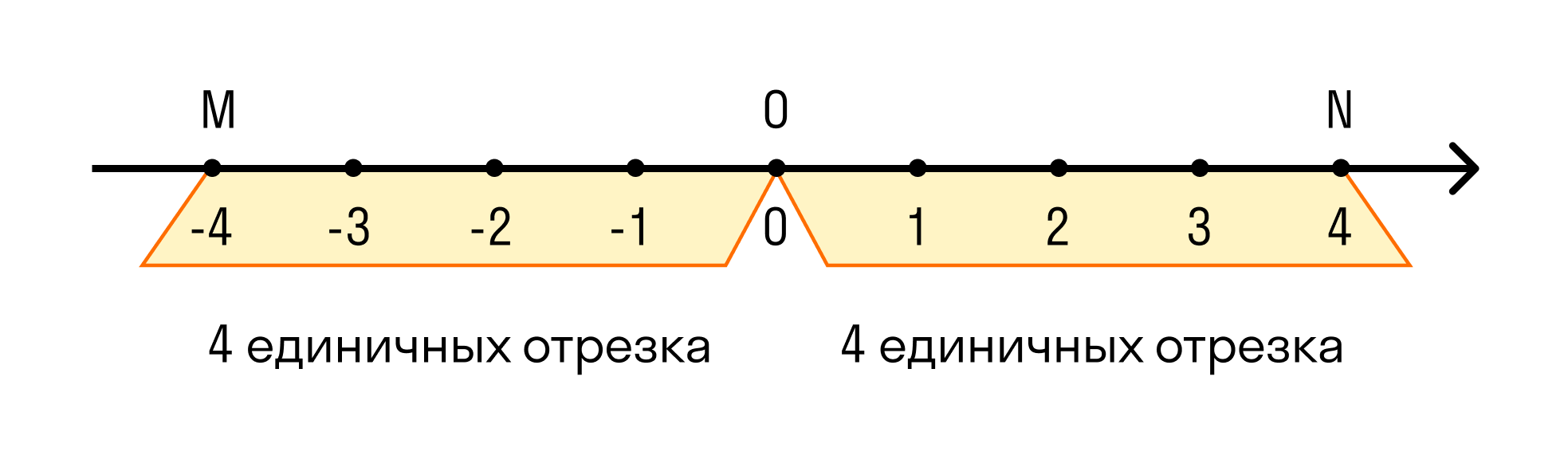
Модулем числа 5 будет 5, т.к. точка В(5) отстоит от начала отсчета на 5 единичных отрезков. Записывают так: |5| = 5.
Расстояние точки М(-6) от начала отсчета О соответствует 6 единичным отрезкам. Число 6 есть модуль числа -6. Записывают так: |-6| = 6.
Модуль числа бывает только положительным. Если рассматривать положительное число и нуль, то модуль их будет равен им же, а если рассматривать отрицательное число – то модуль равен противоположному числу. У противоположных чисел одинаковые модули:
Модуль нуля равен нулю, т.к. точка с координатой нуль совпадает с началом отсчета 0, то есть удалена от нее на 0 единичных отрезков:
Просмотрев определение модуля числа можно сделать вывод, что модуль числа соответствует числу под знаком модуля, не учитывая знак. Это утверждение поясняет из-за чего модуль числа иногда употребляется под значением абсолютной величины числа. Таким образом, модуль числа и абсолютная величина числа – это тоже самое.
К примеру, модуль целого числа −7 можно записать как 



Противоположные числа
Определение противоположных чисел
В 6 классе каждый школьник должен узнать, какие числа являются противоположными. Сейчас расскажем! Для начала построим координатную прямую.
Координатная ось — это прямая линия, на которой отмечено начало координат, задан масштаб и стрелкой указано положительное направление.
Противоположными называются числа, которым соответствуют такие точки на координатной прямой, в которые мы попадем, если отметим одно и то же расстояние от начала отсчета в разных направлениях (положительном и отрицательном). Нуль при этом находится в начале отсчета и противоположен сам себе.
Пары противоположных чисел:
Целые числа включают в себя натуральные числа, числа противоположные натуральным (то есть с отрицательным знаком) и ноль.
Обозначение противоположных чисел
У противоположных чисел есть основные обозначения. Если нам дано число и нужно записать противоположное ему, то для этого нужно использовать знак минус: «-».
Противоположные числа — это два числа, которые отличаются друг от друга знаками.
Примеры противоположных чисел:
Примеры противоположных рациональных чисел:
Свойства противоположных чисел
Перечислим основные свойства противоположных чисел:
Это объясняется тем, что для каждой точки координатной оси существует только одна точка, симметричная ей относительно нуля.
Это свойство следует из того, что противоположные числа находятся на координатной оси по разные стороны от нуля и имеют разные знаки. Исключение: число нуль (0).
Значит, если исходное число со знаком плюс, то противоположное ему будет со знаком минус. А если исходное число является отрицательным, то противоположное ему будет положительным.
Точки координатной прямой, которые соответствуют противоположным числам, находятся на одинаковом расстоянии от начала отсчета.
То есть, такие числа одинаковы по модулю, но имеют разные знаки.
Модуль числа
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Записывайся на занятия по математике для учеников с 1 по 11 классы.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
Оно равно a при а > 0 и −а, при а
Модуль комплексного числа
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
Модуль вещественных чисел
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Закрепим свойства модуля числа, которые мы рассмотрели выше:
Модуль числа
Чтобы понять это определение, подставим вместо переменной a любое число, например 3, и снова прочитаем его:
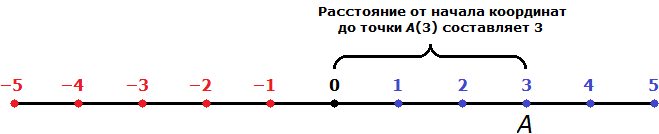
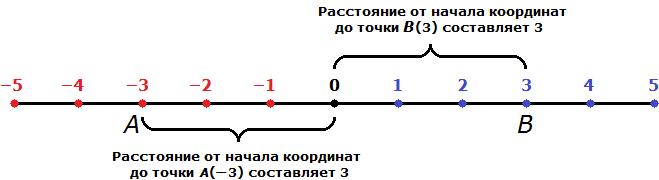
Мóдуль числá 3 — это расстояние от начала координат до точки А( 3 ).
То есть модуль это ни что иное как обычное расстояние. Давайте попробуем увидеть расстояние от начала координат до точки А(3)
Расстояние от начала координат до точки А(3) составляет 3 (три единицы или три шага).
Модуль числа обозначает двумя вертикальными линиями, например:
Модуль числа 3 обозначается так: |3|
Модуль числа 4 обозначается так: |4|
Модуль числа 5 обозначается так: |5|
Читается как «Модуль числа три равен три»
Модулем числа − 3 называют расстояние от начала координат до точки B(− 3 ).
Расстояние от одного пункта до другого не может быть отрицательным. Модуль это тоже расстояние, поэтому тоже не может быть отрицательным.
Читается как «Модуль числа минус три равен три»
«Модуль нуля равен нулю»
Сделаем выводы:
Противоположные числа
Числа, отличающиеся только знаками называют противоположными.
Например, числа −2 и 2 являются противоположными. Они отличаются только знаками. У числá −2 знак минуса, а у числá 2 знак плюса, но мы его не видим, поскольку плюс как говорилось ранее, не записывают.
Еще примеры противоположных чисел:
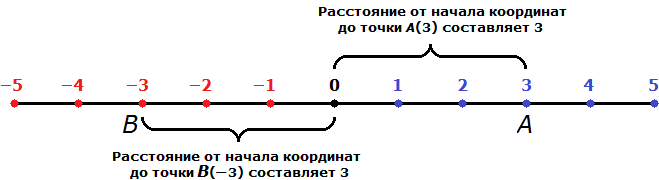
Противоположные числа имеют равные модули. Например, найдём модули чисел −3 и 3
На рисунке видно, что расстояние от начала координат до точек A(−3) и B(3) одинаково равно трём шагам.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
13 thoughts on “Модуль числа”
Все доходчиво и ясно, спасибо.
Благодаря этому сайту, моё желание понимать математику стало реальностью