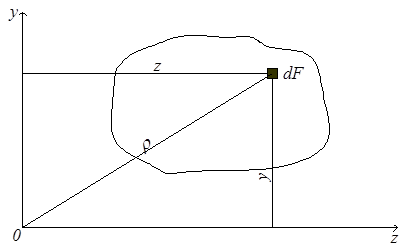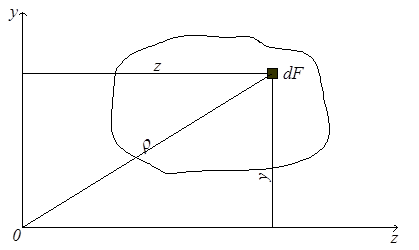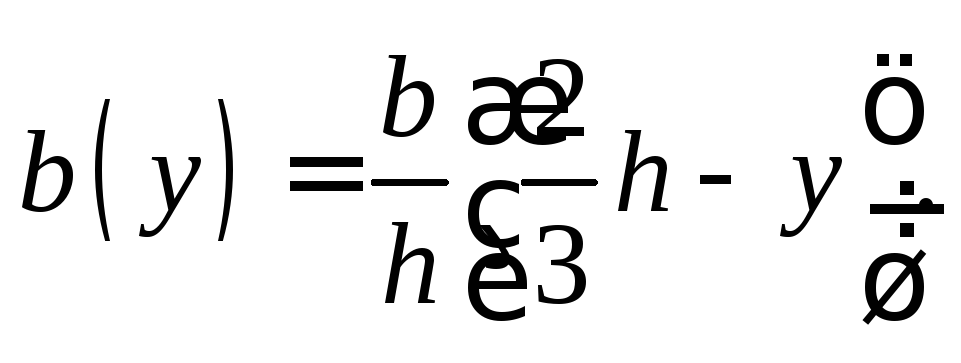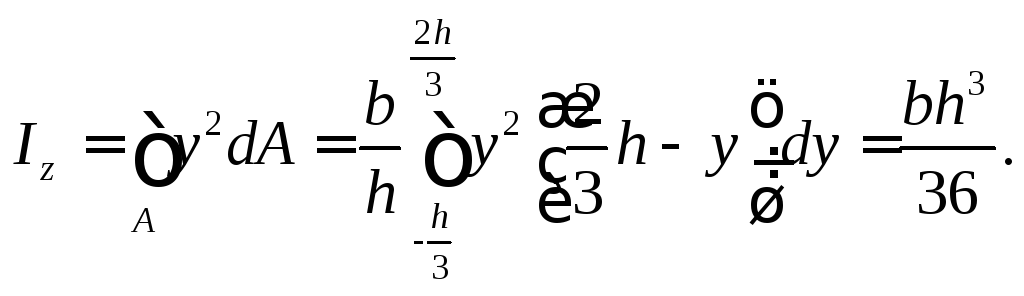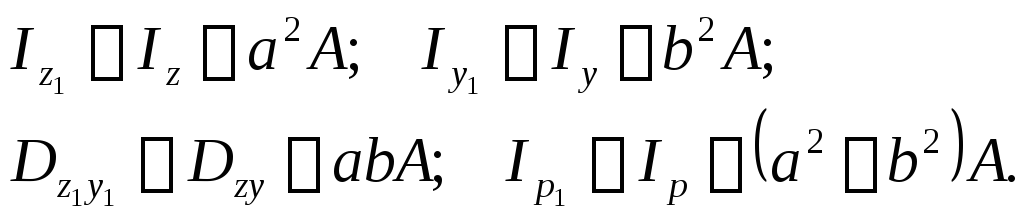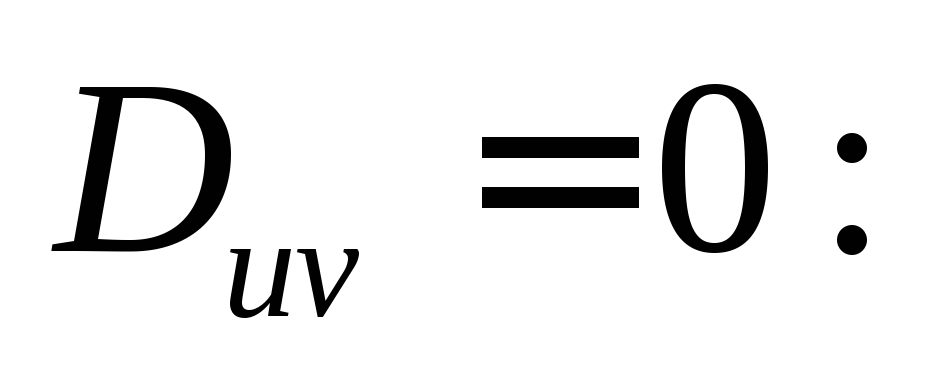какие моменты инерции не всегда положительны

Моменты инерции

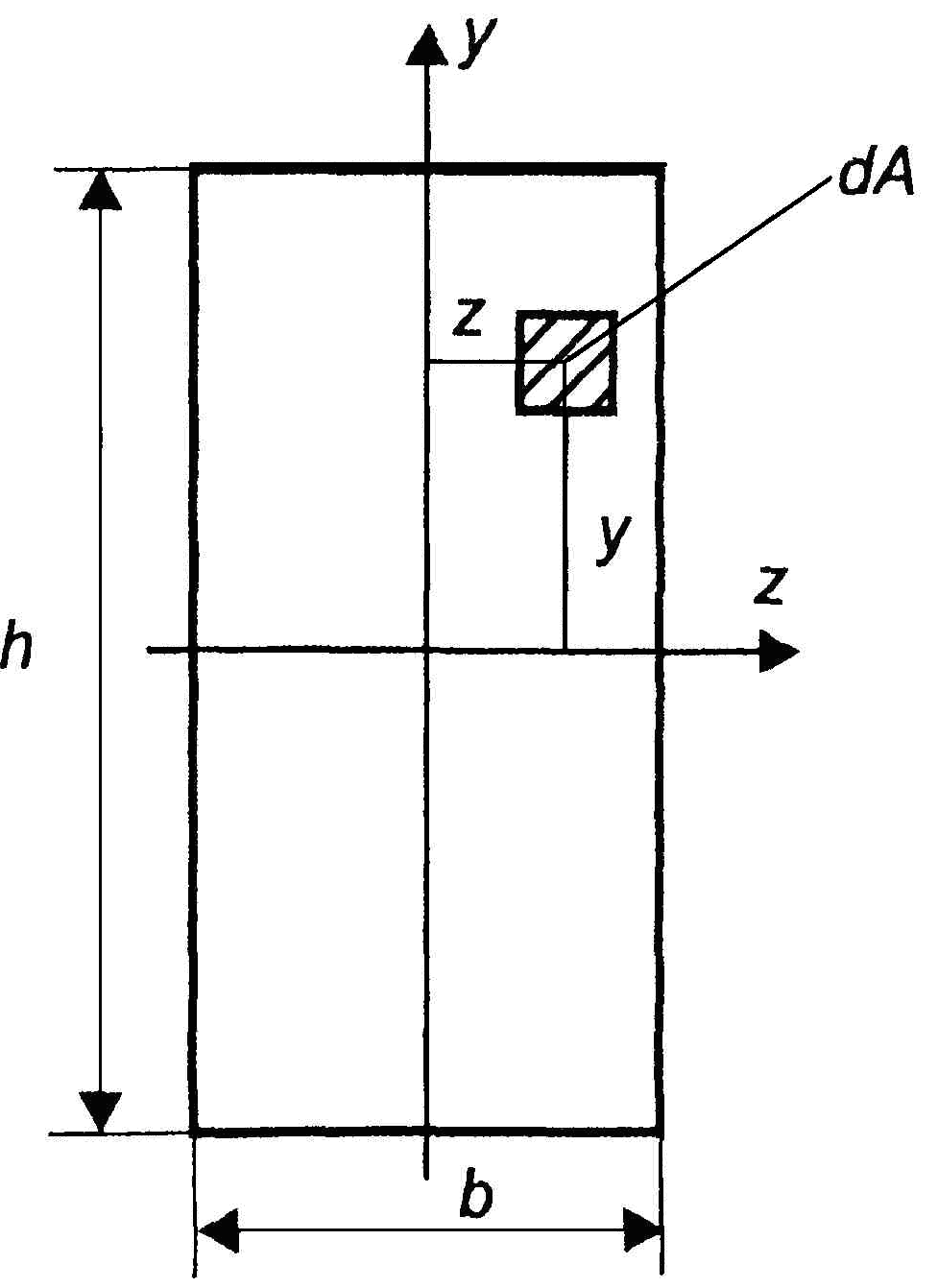
Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).

, . (4.6)

. (4.7)

. (4.8)

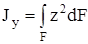
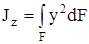
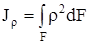
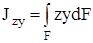
Размерность моментов инерции – единица длины в четвёртой степени (например, см 4 ). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным

в зависимости от положения осей.

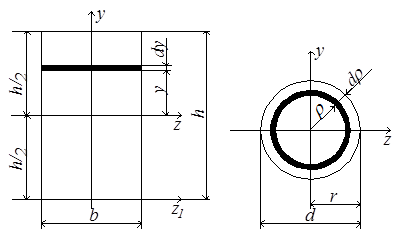
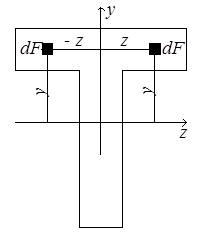Рис.4.5

Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.4.5) и их сумма по всей площади фигуры равна нулю. Главные оси, проходящие через центр тяжести, называются главными центральными осями. Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, Jzy = 0.

Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:

.

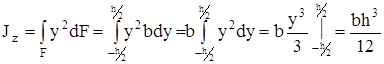
Очевидно, что для определения J_y надо поменять местами стороны прямоугольника.

Главные осевые моменты инерции прямоугольника

, . (4.10)

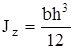
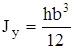
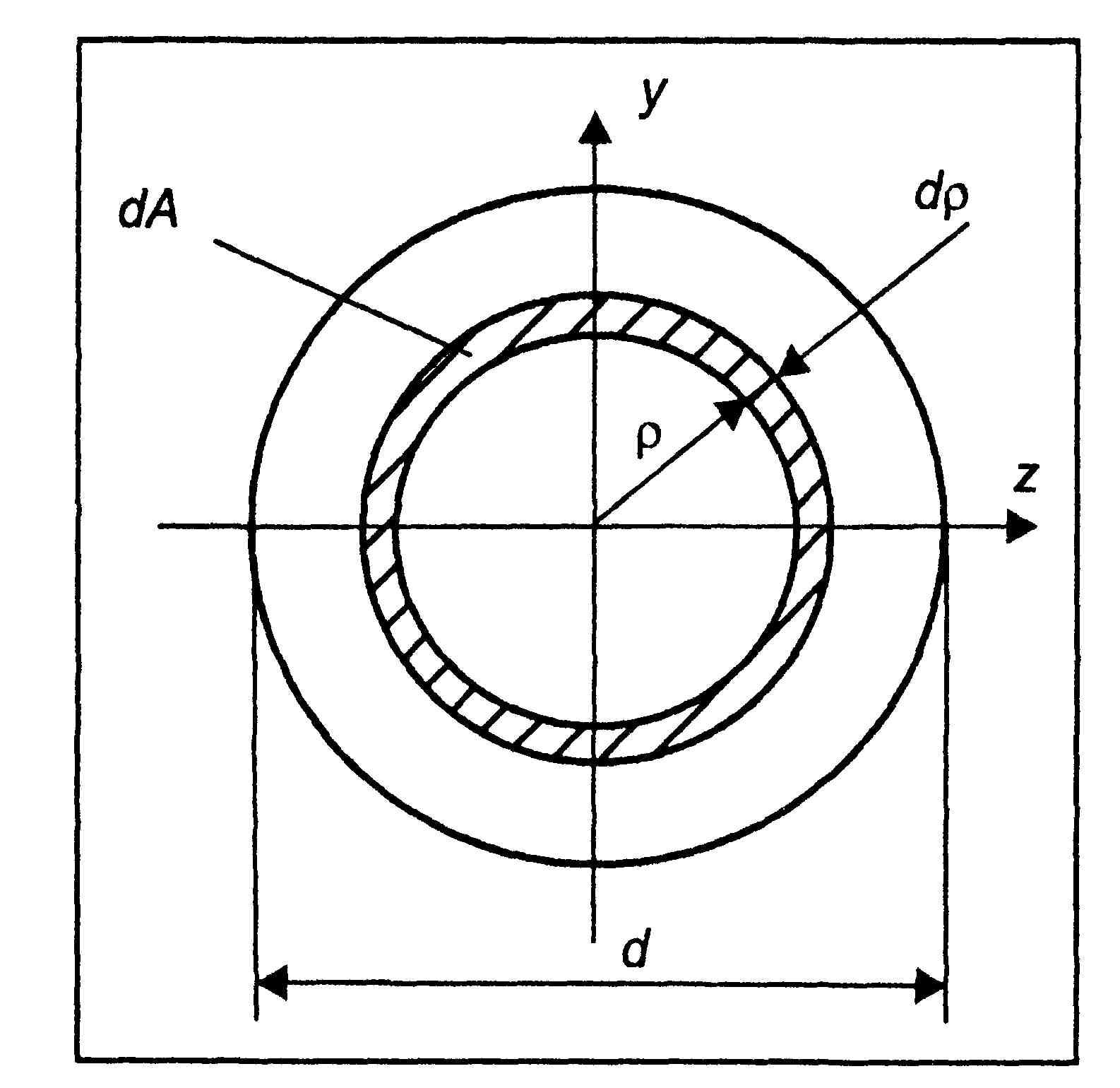
Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)

.

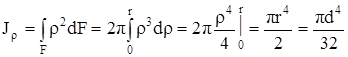
Полярный момент инерции круга

. (4.11)

. (4.12)

Источник

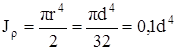
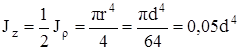
Момент инерции сечения

Меня часто спрашивают: «…а что такое моменты инерции в сопротивлении материалов и зачем они вообще?» Об этом в сегодняшней теме

Моменты инерции сечения из простых фигур

Начнем с моментов инерции простых фигур и на их примере выясним для сложных и составных сечений.

Начать объяснение о том, что такое моменты инерции нужно с того, что спросить, а что такое площадь?

Обычная площадь квартиры, огорода сечения стержня? Зачем она и почему?

Так вот площадь это характеристика которую придумали и вывели для разных фигур, чтобы была возможность сравнивать земельные наделы. Не всегда они были прямоугольные или квадратные. А сравнить кто сколько получил в надел было нужно. Вот и вывели такую закономерность для прямоугольника, что если перемножить стороны — получим величину, которую можно будет сравнить с перемноженной высотой на основание деленное пополам для треугольника или для круга Пи умножить на эр в квадрате )). Т.е. площади простых фигур

Что касается моментов инерции в сопротивлении материалов, то тут они появились, когда стало понятно, что есть какая то геометрически измеримая величина для разных форм сечения, которая позволит сравнить сопротивляемость этих сечений изгибу.

Проще говоря бревно, которое выполняет роль балки и изгибается может иметь форму прямоугольника, квадрата или круга, а нам нужно сравнить их сопротивляемость изгибу. Вот для этих целей выводили формулу напряжений и оказалось, что в числителе оказался изгибающий момент, а в знаменателе момент инерции:

Деформированное и не деформированное состояния балки при расчете на изгиб

на балке изображены главные центральные оси z y

прогибы для таких балок будут разными относительно осей z и y, т.к. моменты инерции будут разные.

Вывод моментов инерции для простых фигур

Так вот ниже я приведу видео уроки, плейлист, в котором один за одним выведены моменты инерции для простых фигур, а именно для прямоугольника, треугольника и круга. А затем приводится стандартный расчет моментов инерции для более сложной фигуры, которая состоит из нескольких простых. Всегда сложную фигуру можно разбить на несколько простых. Исходя из этого расчет и ведется.

Моменты инерции измеряются в единицах длины в 4 степени, т.е. см⁴ или м⁴. Чаще всего используется см⁴, т.к. такие единицы измерения приведены в сортаменте прокатной стали.

Момент инерции, это величина, которая показывает сопротивляемость сечения изгибу. На примере линейки хорошо понятно что изгиб в одной плоскости и изгиб в другой плоскости будут сильно отличаться, хотя площадь сечения не меняется. Вот это и было выведено в формуле для напряжений и для прогибов. Что величина, которая сопротивляется изгибающему моменту есть интеграл до координаты центра тяжести площадки в квадрате на площадь элементарной площадки.

Центральными осями называют оси, которые проходят через центр тяжести сечения

Главные оси располагаются в сечении таким образом, что центробежный момент относительно них равен нулю. Т.е. это максимальный и минимальный осевые моменты инерции

Оси, которые проходят через центр тяжести сечения и центробежный момент инерции относительно них равен нулю. При этом данные осевые моменты инерции являются экстремальными, т.е. имеют максимальное и минимальное значение. Именно относительно этих осей ведут расчет и к ним приводят нагрузки. Т.е. если какое нибудь внешнее усилие проходит в стороне от главных центральных осей. Это усилие переносят соблюдая правила переноса к главным центральным осям. Только после этого рассматривают действие сил и находят внутренние усилия относительно главных центральных осей инерции.

При вычислении моментов инерции осевых, при переходе от одних осей к другим появляется центробежный момент инерции, как составляющая пары осевых моментов инерции. И только для главных осей центробежные моменты инерции равны нулю. Именно эти оси мы и отыскиваем в наших расчетах. Поэтому мы ищем величину центробежного момента инерции для не главных осей и из свойства, что главные центральные оси это такие оси, относительно которых центробежный момент инерции равен нулю, находим положение главных центральных осей.

Моменты инерции для прямоугольника

#Сопромат, Моменты инерции. Прямоугольник. Вывод моментов инерции для прямоугольника.

Сопротивление материалов и Моменты инерции для прямоугольника. Понятие моментов инерции, формулы и вывод для прямоугольника. Осевые центробежный моменты инерции. для треугольника вывод моментов инерции в этом видео: https://www.youtube.com/embed/_pixohVoc-4?vq=hd720 Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

моменты инерции для прямоугольника для главных центральных осей равны, формула

моменты инерции для прямоугольника для осей проходящих через основные размеры равны, формула

Моменты инерции для треугольника

Сопротивление материалов, Моменты инерции для треугольника. Сопромат вывод моментов инерции

Сопротивление материалов и Моменты инерции для треугольника. Сопромат вывод моментов инерции для простых фигур. Моменты инерции для треугольника. Моменты инерции для осей в треугольнике, которые проходят через основные размеры. Вывод и пояснение к этой теме сопротивления материалов. для прямоугольника вывод моментов инерции в этом видео: https://www.youtube.com/watch?v=v1TE1UW_sRE&feature=youtu.be‎ Тема моментов инерции возникла в связи стем, что для определения напряжений при изгибе понадобилась геометрическая характеристика, которая сопротивляется внутреннему усилию (изгибающему моменту). В результате вывода формулы напряжений и появилась эта формула, выраженная через интеграл от квадрата координаты помноженной на площадь элементарной площадки. Эту геометрическую характеристику и назвали моментом инерции. пройти полный курс обучения сопромату и строймеху онлайн, по скайпу Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2018-04-09

Моменты инерции треугольника относительно произвольых осей
Моменты инерции треугольника относительно центральных осей

Момент инерции круга. Моменты инерции простых фигур. #сопромат

Вывод моментов инерции для круга. Видео урок из темы «Моменты инерции простых фигур». В видео приведен вывод момента инерции полярного, в полярной системе координат Ip Затем выведены моменты инерции осевые Iz, Iy. Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Моменты инерции. Оси центральные и главные. Что это и где. #сопромат

Центральные оси — любая пара взаимно перпендикулярных осей, которые проходят через центр тяжести фигуры Главные оси — оси для которых центробежный момент инерции равен нулю, а осевые моменты имеют максимум и минимум. Об этом и многом другом в видео уроке по моментам инерции в сопротивлении материалов Задать вопросы можно: — через сайт: https://stroymex.online — skype: zabolotnyiAN — email: zabolotnyiAN@gmail.com — комменты к видео — Телеграм https://t.me/AleksanderCrafts Телеграм канал: https://t.me/sroymexOnline Не тратьте время зря, задавайте вопросы. Узнайте стоимость обучения: https://stroymex.online/usloviya-i-tsena-onlayn-obucheniya-sopromat-i-stroymeh Получите первую консультацию бесплатно! Facebook: https://www.facebook.com/SopromatOnline

2019-09-14

Источник

Момент инерции для чайников: определение, формулы, примеры решения задач

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции».

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела. Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm, то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m, вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r, а масса – dm. Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи. Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и решению задач.

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе. Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Источник

Может ли момент инерции быть отрицательным

Моментом инерции называется характеристика, отличающаяся от статического момента тем, что координата входит в подынтегральное выражение в квадрате (рис.4.4). Моменты инерции бывают осевые или экваториальные – формула (4.6.), полярный – (4.7) и центробежный – (4.8).

, . (4.6)

. (4.7)

. (4.8)

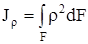
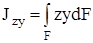
Размерность моментов инерции – единица длины в четвёртой степени (например, см 4 ). Отметим, что осевой и полярный моменты инерции всегда положительны. Центробежный момент инерции может быть положительным или отрицательным

в зависимости от положения осей.

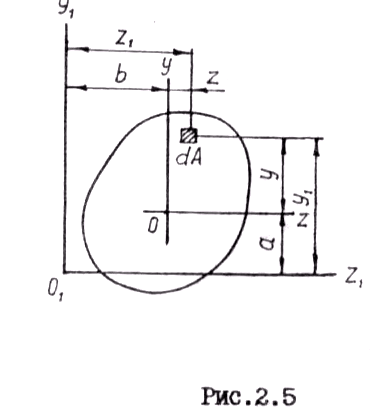
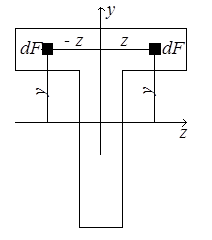Рис.4.5

Очевидно, постепенно поворачивая оси, можно найти такое их положение, при котором центробежный момент инерции равен нулю. Такие оси называются главными осями инерции. Две взаимно перпендикулярные оси, из которых хотя бы одна является осью симметрии фигуры, всегда будут её главными осями инерции, поскольку в этом случае каждой положительной величине zydF соответствует такая же отрицательная по другую сторону от оси симметрии (рис.4.5) и их сумма по всей площади фигуры равна нулю. Главные оси, проходящие через центр тяжести, называются главными центральными осями. Вычислим моменты инерции прямоугольника относительно главных центральных осей (рис.4.6,а). Оси z и y – главные, т.к. они являются осями симметрии, Jzy = 0.

Для определения осевого момента инерции относительно оси z выделим элементарную площадку в виде полоски, параллельной оси z:

.

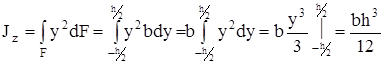
Очевидно, что для определения J_y надо поменять местами стороны прямоугольника.

Главные осевые моменты инерции прямоугольника

, . (4.10)

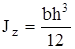
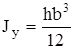
Вычислим полярный момент инерции круга относительно его центра, а также осевой момент инерции относительно центральной оси. При вычислении полярного момента инерции выделим элементарную площадку в виде тонкого кольца толщиной dρ (рис.4.6,б) и подсчитаем по формуле (4.7)

.

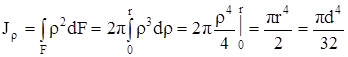
Полярный момент инерции круга

. (4.11)

. (4.12)

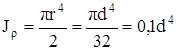
Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8910 – | 7222 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Моментами инерции сечений называются интегралы следующего вида:

– осевой момент инерции сечения относительно оси у;

– осевой момент инерции сечения относительно оси z;

– центробежный момент инерции сечения;

– полярный момент инерции сечения.

3.2.1. Свойства моментов инерции сечения

Размерность моментов инерции – [длина 4 ], обычно [м 4 ] или [см 4 ].

Осевые и полярный моменты инерции всегда положительные. Центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения.

Оси симметрии всегда главные. Если из двух взаимно перпендикулярных осей хотя бы одна является осью симметрии, то обе оси главные.

Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения.

Полярный момент инерции равен сумме осевых моментов инерции.

.

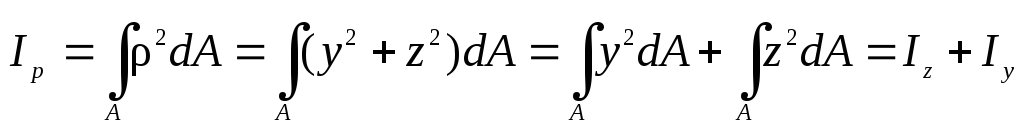
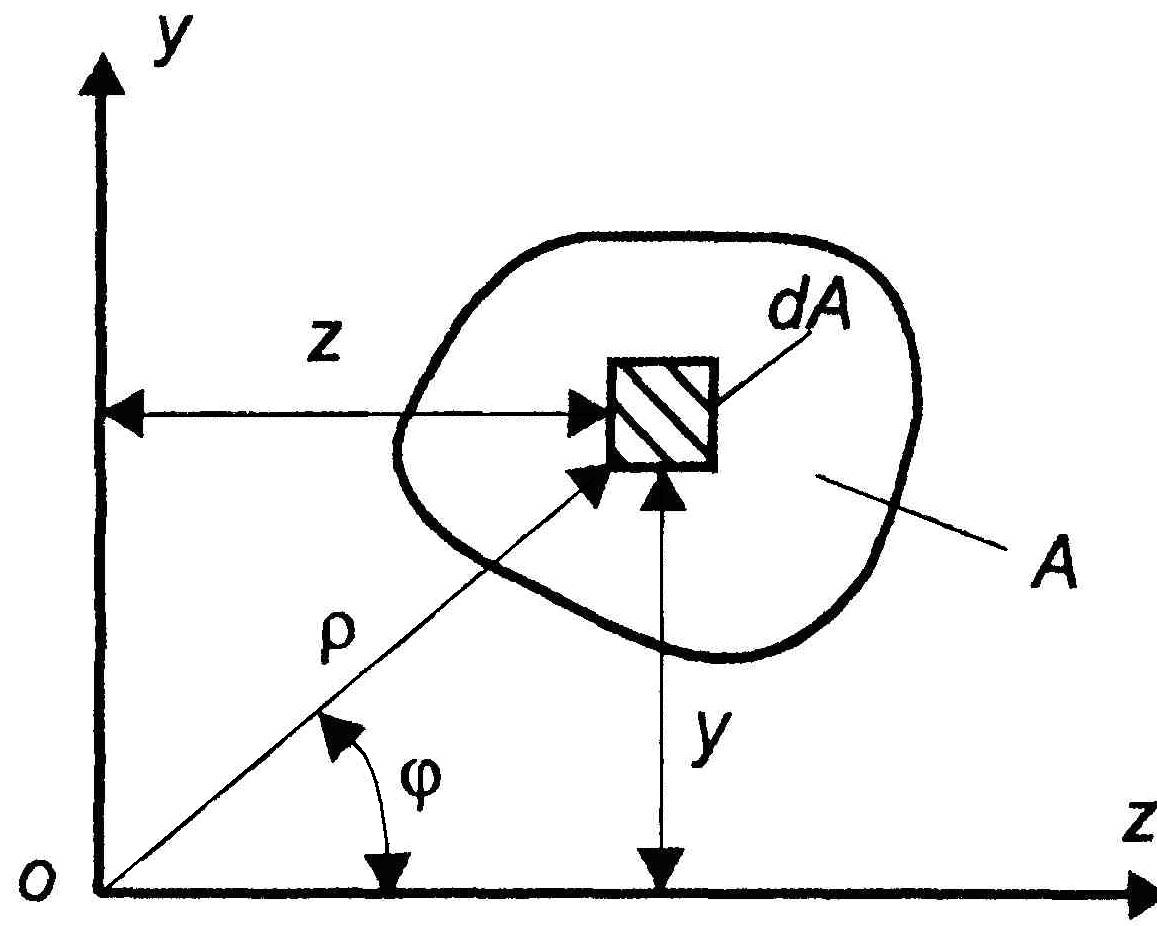
Рис. 6. Связь полярных и декартовых координат

3.2.2. Моменты инерции простейших фигур

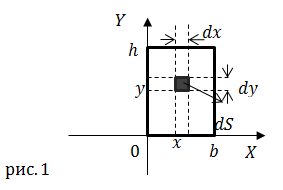
В прямоугольном сечении (рис. 7) выберем элементарную площадку dA с координатами y и z и площадью dA = dydz.

Рис. 7. Прямоугольное сечение

Осевой момент инерции относительно оси у

.

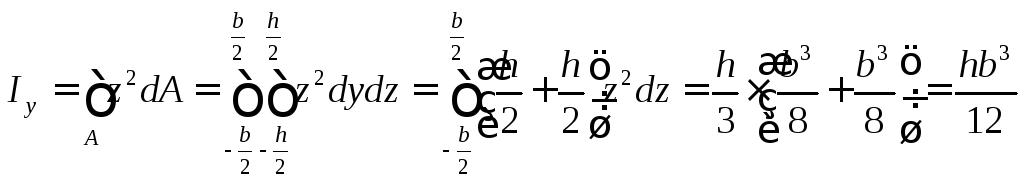
Аналогично получаем момент инерции относительно оси z:

Поскольку у и z – оси симметрии, то центробежный момент D_zy = 0.

Для круга диаметром d вычисления упрощаются, если учесть круговую симметрию и использовать полярные координаты. Возьмем в качестве элементарной площадки бесконечно тонкое кольцо с радиусом ρ и толщиной dρ (рис. 8). Его площадь dA = 2πρdρ. Тогда полярный момент инерции:

.

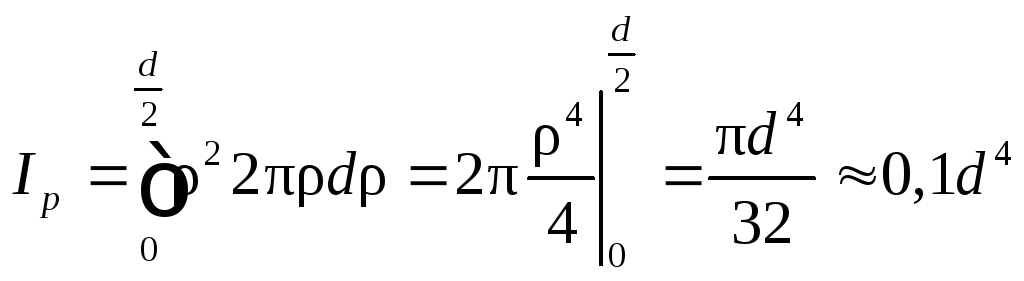
Рис. 8. Круглое сечение

Как показано выше, осевые моменты инерции относительно любой центральной оси одинаковы и равны

.

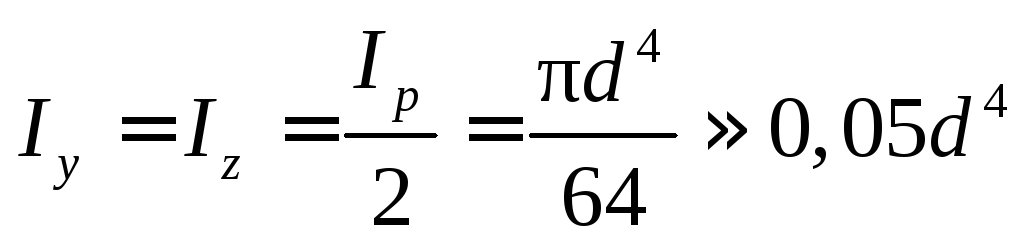
Момент инерции кольца находим как разность моментов инерции двух кругов – наружного (с диаметром D) и внутреннего (с диаметром d):

Момент инерции I_zтреугольникаопределим относительно оси, проходящей через центр тяжести (рис. 9). Очевидно, ширина элементарной полоски, находящейся на расстоянииуот осиz, равна

Рис. 9. Треугольное сечение

3.3. Зависимости между моментами инерции относительно параллельных осей

При известных величинах моментов инерции относительно осей z и у определим моменты инерции относительно других осей z₁ и y₁, параллельных заданным. Пользуясь общей формулой для осевых моментов инерции, находим

Если оси z и y центральные, то 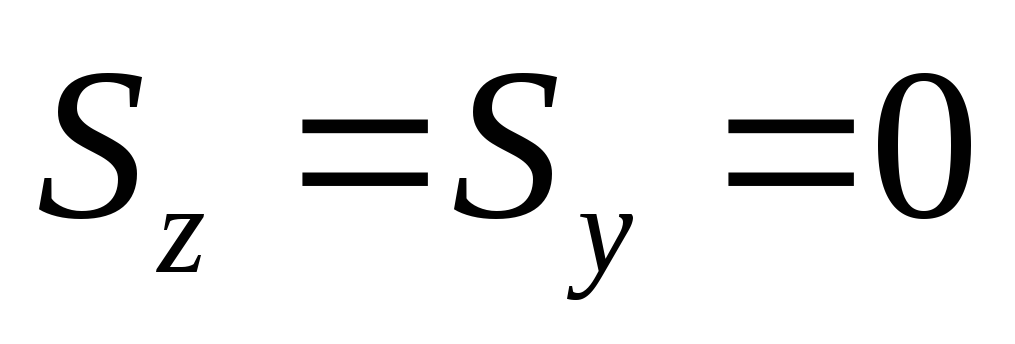, и

Из полученных формул видно, что моменты инерции относительно центральных осей (когда 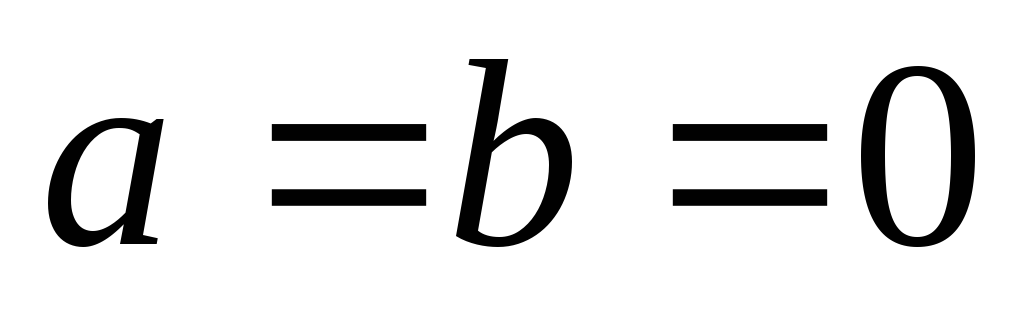) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.

3.4. Главные оси и главные моменты инерции

При повороте осей на угол α центробежный момент инерции становится равным

.

Определим положение главных главных осей инерции u, v относительно которых

,

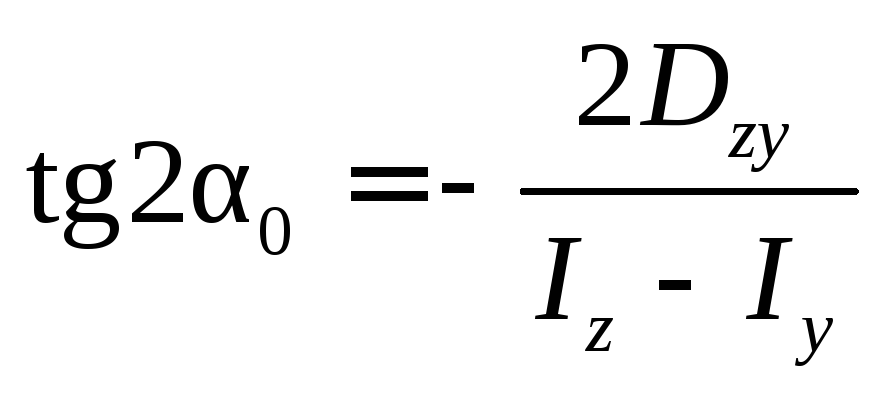
где α – угол, на который надо развернуть оси y и z, чтобы они стали главными.

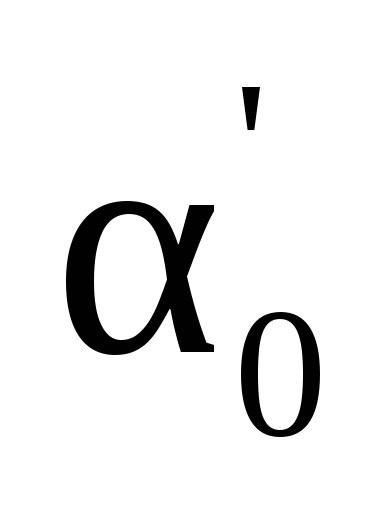
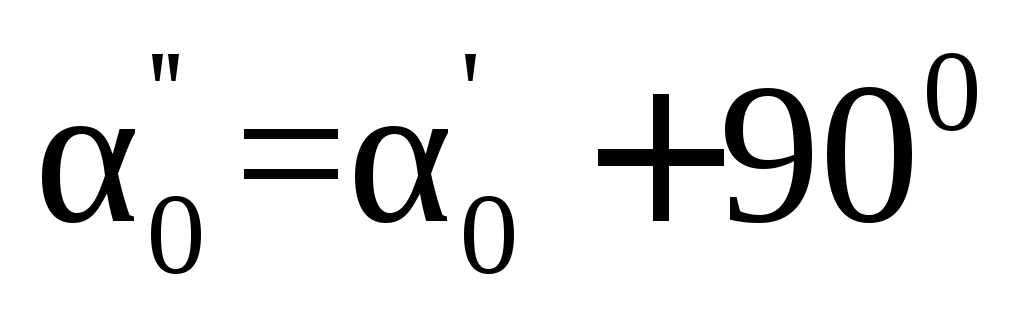
Поскольку формула дает два значения углаи, то существуют две взаимно перпендикулярные главные оси. Ось максимума всегда составляет меньший угол () с той из осей (z или y), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси z против хода часовой стрелки.

Моменты инерции относительно главных осей называются главными моментами инерции. Можно показать, что они

.

Знак плюс перед вторым слагаемым относится к максимальному моменту инерции, знак минус – к минимальному.

Центробежный момент инерции тела

Допустим, что имеется система координат с началом в точке O и осями OX; OY; OZ. По отношению к данным осям центробежными моментами инерции (произведениями инерции) называются величины , которые определяются равенствами:

где – массы материальных точек, на которые разбивают тело; – координаты соответствующих материальных точек.

Центробежный момент инерции обладает свойством симметрии, это следует из его определения:

Если тело можно считать сплошным (непрерывным), то определение центробежного момента инерции записывают как:

Центробежные моменты тела могут быть положительными и отрицательными, при определённом выборе осей OXYZ они могут обращаться в ноль.

Для центробежных моментов инерции существует аналог теоремы Штейнберга. Если рассмотреть две системы координат: и . Одна из этих систем имеет начало координат в центе масс тела (точка C), оси систем координат являются попарно параллельными (). Пусть в системе координат координатами центра масс тела являются (), тогда:

где – масса тела.

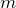
Главные оси инерции тела

Пусть однородное тело имеет ось симметрии. Построим координатные оси так, чтобы ось OZ была направлена вдоль оси симметрии тела. Тогда, как следствие симметрии каждой точке тела с массой и координатами соответствует точка, имеющая другой индекс, но такую же массу и координаты: . В результате получаем, что:

так как в данных суммах все слагаемые имеют свою равную по величине, но противоположную по знаку пару. Выражения (4) эквивалентны записи:

Мы получили, что осевая симметрия распределения масс по отношению к оси OZ характеризуется равенством нулю двух центробежных моментов инерции (5), которые содержат среди своих индексов наименование этой оси. В таком случае ось OZ называется главной осью инерции тела для точки О.

Главная ось инерции не всегда является осью симметрии тела. Если тело обладает плоскостью симметрии, то любая ось, которая перпендикулярна этой плоскости, является главной осью инерции для точки O, в которой ось пересекает рассматриваемую плоскость. Равенства (5) отображают условия того, что ось OZ является главной осью инерции тела для точки O (начала координат). Если выполняются условия:

то ось OY будет для точки O главной осью инерции.

В том случае, если выполняются равенства:

то все три координатные оси системы координат OXYZ являются главными осями инерции тела для начала координат.

Моменты инерции тела по отношению к главным осям инерции называются главными моментами инерции тела. Главные оси инерции, которые построены для центра масс тела, носят название главных центральных осей инерции тела.

Если тело обладает осью симметрии, то она является одной из главных центральных осей инерции тела, поскольку центр масс находится на этой оси. В том случае, если тело имеет плоскость симметрии, то ось, нормальная к этой плоскости и проходящая через центр масс тела является одной из главных центральных осей инерции тела.

Понятие главных осей инерции в динамике твердого тела имеет существенное значение. Если вдоль них направить оси координат OXYZ, то все центробежные моменты инерции становятся равными нулю, при этом значительно упрощаются формулы, которые следует применять при решении задач динамики. С понятием о главных осях инерции связано решение задач о динамическом уравнении тела находящегося во вращении и о центре удара.

Момент инерции тела ( и центробежный в том числе) в международной системем единиц измеряются в:

Центробежный момент инерции сечения

Центробежным моментом инерции сечения (плоской фигуры) относительно двух взаимно нормальных осей (OX и OY) называют величину, равную:

выражение (8) говорит о том, что центробежный момент инерции сечения относительно взаимно перпендикулярных осей есть сумма произведений элементарных площадок () на расстояния от них до рассматриваемых осей, по всей площади S.

Единицей измерения моментов инерции сечения в СИ является:

Центробежный момент инерции сложного сечения по отношению к любым двум взаимно нормальным осям равен сумме центробежных моментов инерции составляющих его частей относительно этих осей.

Примеры решения задач

Для определения центробежного момента инерции выделим из имеющегося прямоугольника элемент его площади (рис.1) , площадь которой равна:

На первом этапе решения задачи найдем центробежный момент инерции () вертикальной полосы, имеющей высоту и ширину , которая находится на расстоянии от оси Y (учтем, что при интегрировании для всех площадок в избранной вертикальной полоске величина является постоянной):

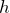
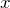
На втором этапе решения задачи проинтегрируем, двигаясь по горизонтали, учитывая, что :

Источник