Расчет энергосиловых параметров прокатки

Методика расчета энергосиловых параметров прокатки

7. Методика расчета энергосиловых параметров прокатки

Расчет энергосиловых параметров выполним по ходу прокатки. Для начала выполним расчет коэффициентов вытяжки и скоростного режима прокатки [3].

Площадь полосы в калибре определим по:

где В-ширина калибра;

d – толщина стенки калибра;

a_o – толщина открытого фланца у вершины калибра;

b_o – толщина открытого фланца у основания калибра;

h_o – высота открытого фланца;

a_з – толщина закрытого фланца у вершины калибра;

b_з – толщина закрытого фланца у основания калибра;

h_з – высота закрытого фланца.

Для расчета скоростного режима и энергосиловых параметров прокатки фасонные полосы пересчитываем на соответственные прямоугольные по методу приведенной высоты:

где ω – площадь полосы в калибре;

Определим катающие диаметры валков. Расчет следует вести при максимальных диаметрах валков, чтобы определить максимальную энергосиловую загрузку оборудования стана.

где D₀ – максимальный диаметр бочки валков (см. табл. 2.1);

Н_с – приведенная высота фасонной полосы.

Коэффициент вытяжки в разрезном калибре:

где ω_i-1 – площадь полосы задаваемой в калибр;

ω_i – площадь полосы выходящей из калибра.

Конечную скорость прокатки определим, исходя из максимально допустимой скорости валков в чистовой клети с учетом запаса на регулирование в связи с переточкой валков в размере 8%:

м/с, (5)

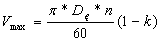
где D_к – катающий диаметр валков;

n – максимальная чистота вращения валков;

k – коэффициент запаса на регулирование в связи с переточкой валков.

Частота вращения валков:

об/мин, (6)

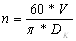
где V – скорость вращения валков;

D_к – катающий диаметр.

Найденную частоту вращения валков нужно сравнить с допустимой (см. табл. 2.1).

Найдем скорости в остальных калибрах из условия постоянства секундных объемов металла, проходящих через калибры этих клетей:

м/с, (7)

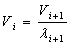
где V – скорость вращения валков;

λ – коэффициент вытяжки.

Выполняем расчет энергосиловых параметров. Определим значения усилия, крутящие моменты и температурный режим прокатки.

Определим абсолютное изменение приведенной высоты:

Определим среднее значение приведенных высот в калибре:

где Н_0с – приведенная высота в предыдущем калибре;

Н_1с – приведенная высота в данном калибре.

, (10)

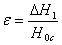
где ΔН₁ – абсолютное изменение приведенной высоты;

Н_0с – приведенная высота в предыдущем калибре.

Скорость деформации металла:

где n – частота вращения валков;

ε – относительное обжатие;

D_к – катающий диаметр;

Н_с – приведенная высота в калибре.

Длина очага деформации:

мм. (12)

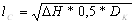
Рассчитаем контактную площадь прокатки:

где B₀ – ширина раската перед входом в данный калибр;

B₁ – ширина раската;

l_c – длина очага деформации.

Найдем длину раската по проходам. При длине исходной заготовки 5 метров из описания технологии прокатки на данном стане.

Длины раската по проходам:

где L_i-1 – длина предыдущего раската;

λ_i – коэффициент вытяжки.

Определим сопротивление деформации стали 70 по методу термомеханических коэффициентов В.И. Зюзина:

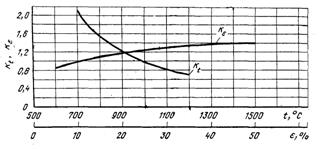
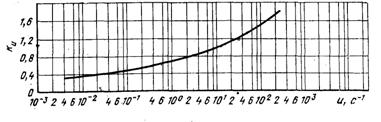
К_t, К_ε, К_u – термомеханические коэффициенты, учитывающие соответственно влияние температуры прокатываемого металла, степени и скорости деформации. Эти коэффициенты определяются по формулам или кривым, построенным для каждой марки стали. В нашем случае для стали 10 пс определим эти коэффициенты по рисункам 7.1 и 7.2.

Рис. 7.1. Температурный К_t и степенной К_ε коэффициенты стали 20ПС

Рис. 7.2. Скоростной К_u коэффициент стали 20ПС

Для стали 20 пс σ_од = 82,32 МПа. [12]

Определяем температуру раската перед входом во вторую клеть. Для этого рассчитаем время охлаждения раската, которое складывается из паузы на передачу раската от одной клети к другой и машинного времени прокатки.

Рассчитаем время охлаждения раската:

сек, (16)

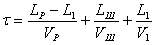
где L_p – длина рольганга;

V_р – скорость рольганга;

V_ш – скорость шлепера;

V₁ – скорость прокатки в данной клети.

Найдем повышение температуры металла вследствие перехода механической энергии деформации в теплоту:

Δt_д = 0,183×σ×lnλ 0 C, (17)

где σ – сопротивление деформации стали;

λ – коэффициент вытяжки.

Рассчитаем периметр поперечного сечения раската после прохода:

где Н_с – приведенная высота в калибре;

Тогда на основе использования метода А.И. Целикова изменение температуры раската за время прокатки в калибре и перемещения к следующему калибру составит:

0 С, (19)

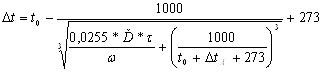
где t₀ – температура раската перед входом в рассматриваемый калибр;

П – периметр поперечного сечения раската после прохода;

τ – время охлаждения раската;

ω – площадь поперечного сечения раската после прохода;

Δt_д – повышение температуры металла вследствие перехода механической энергии деформации в теплоту.

Температура металла перед заходом в следующую клеть:

где t_i-1 – температура прокатки в предшествующей клети;

Δt – изменение температуры раската за время прокатки в калибре и перемещения к следующему калибру составит.

Рассчитаем контактное давление прокатки по методу В.С. Смирнова:

где n_σ – коэффициент напряженного состояния, учитывающий влияние на контактное давление внешнего трения;

n_ж – коэффициент, учитывающий влияние внешних зон по отношению к геометрическому очагу деформации;

n_ф – коэффициент формы профиля.

Найдем коэффициент напряженного состояния:

n_σ = 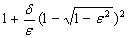, (22)

где δ – коэффициент учитывающий влияние контактного трения на форму очага деформации;

ε – относительное обжатие.

Определим коэффициент учитывающий влияние контактного трения на форму очага деформации:

, (23)

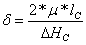
где μ – коэффициент внешнего трения;

l_c – длина очага деформации;

ΔН_с – абсолютное изменение приведенной высоты.

Коэффициент внешнего трения:

μ = 0,55 – 0,00024×t, (24)

где t – температура деформируемого металла.

Найдем отношение длины очага деформации к среднему значению приведенной высоты: .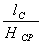

Определим значение коэффициента, учитывающего влияние внешних зон по отношению к геометрическому очагу деформации:

n_ж = 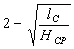, (25)

где 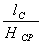– фактор формы очага деформации.

Найдем коэффициент формы профиля:

n_ф = 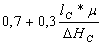, (26)

где l_c – длина очага деформации;

μ – коэффициент внешнего трения;

ΔН_с – абсолютное изменение приведенной высоты.

Рассчитаем усилие прокатки:

где р – контактное давление прокатки;

F – контактная площадь прокатки.

Определим коэффициент плеча приложения усилия прокатки по формуле М.А. Зайкова – Н.А. Федорова:

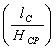
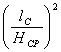
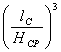
φ_п = 5,85 – 11∙ + 7,35∙ – 1,58∙, (28)

где 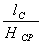– фактор формы очага деформации.

Рассчитаем крутящий момент деформации:

Ограничения по скоростному режиму прокатки проверяем по формулам (26) и (27) с учетом коэффициента загрузки электродвигателей стана.

Коэффициент загрузки электродвигателей стана по усилию прокатки:

, (30)

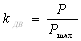
где Р – усилие прокатки;

Р_max – максимально допустимое усилие прокатки.

м/с; (31)

м/с, (32)

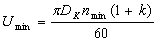
где D_к – катающий диаметр;

n_max, n_max – соответственно максимально возможные и минимальные частоты вращения валков (см. табл. 2.1);

k – коэффициент загрузки электродвигателей стана.

Определим часовую производительность стана:

, (33)

Источник

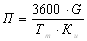
Расчет энергосиловых параметров прокатки

8. Расчет энергосиловых параметров прокатки

Исходными данными для расчета энергосиловых параметров служат данные расчета калибровки.

Расчет энергосиловых параметров выполним по методика приведенной выше.

По формуле (1) рассчитаем площадь полосы в каждом калибре:

ω₁ = 307×73 + 2 ((60 + 125)×96,4/2 + (66,3 + 137,5)×87,2/2) = 58016 мм 2 ;

ω₂ = 317×48,3 + 2 ((34 + 69)×88,4/2 + (52 + 51)×88,4/2) = 33521,5 мм 2 ;

ω₃ = 328×30,8 + 2 ((20 + 44)×89,6/2 + (30 + 41,4)×80,4/2) = 21577,4 мм 2 ;

ω₄ = 338×19,7 + 2 ((14 + 30,3)×81,6/2 + (18 + 26)×81,6/2) = 13864 мм 2 ;

ω₅ = 348×13 + 2 ((7,4 + 20)×82,8/2 + (12,4 + 18,8)×73,6/2) = 9089 мм 2 ;

ω₆ = 355×9,55 + 2 ((6,04 + 16)×74,8/2 + (7,4 + 14,6)×74,8/2) = 6684,4 мм 2 ;

ω₇ = 358×8,3+ 2 ((4,5 + 13,56)×76/2 + (6,04 + 14,4)×66,8/2) = 5709,4 мм 2 ;

Для расчета скоростного режима и энергосиловых параметров прокатки фасонные полосы пересчитываем на соответственные прямоугольные по методу приведенной высоты. Рассчитаем по формуле (2) значения приведенной высоты:

Н_с1 = 58016/307 = 189 мм; Н_с2 = 33521,5/316,8 = 105,8 мм;

Н_с3 = 21577,4/328 = 66 мм; Н_с4 = 13864/338 = 41 мм;

Н_с5 = 9089 /348 = 26 мм; Н_с6 = 6684,4/355 = 19 мм;

Н_с7 = 5709,4/358 = 16 мм; Н_с8 = 5294/360 = 15 мм.

Определим катающие диаметры валков. Расчет будем вести при максимальных диаметрах валков (см. табл. 2.1), чтобы определить максимальную энергосиловую загрузку оборудования стана. По формуле (3) рассчитаем катающие диаметры:

D₁ = 1000 – 189 = 811 мм; D₂ = 1000 – 105,8 = 894,2 мм;

D₃ = 1000 – 66 = 934 мм; D₄ = 800 – 41 = 759 мм;

D₅ = 800 – 26 = 774 мм; D₆ = 800 – 19 = 781 мм;

D₇ = 800 – 16 = 784 мм; D₈ = 800 –15 = 785 мм.

Найдем коэффициент вытяжки в калибрах по формуле (4):

λ₁ = 89925/58016 = 1,55; λ₂ = 58016/ 33521,5 = 1,73; λ₃ = 33521,5/ 21577,4 = 1,55;

λ₄ = 21577,4/ 13864 = 1,55; λ₅ = 13864/ 9089 = 1,53; λ₆ = 9089/ 6684,4 = 1,36;

λ₇ = 6684,4/ 5709,4 = 1,17; λ₈ = 5709,4/ 5294 = 1,08.

Определим по формуле (5) конечную скорость прокатки в восьмой клети, исходя из максимально допустимой скорости валков в чистовой клети с учетом запаса на регулирование в связи с переточкой валков в размере 5%:

м/с.

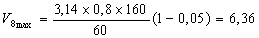
Принимаем конечную скорость прокатки 6,4 м/с.

Найдем по формуле (7) скорости в остальных калибрах из условия постоянства секундных объемов металла:

м/с; м/с; м/с; м/с;

м/с; м/с; м/с.

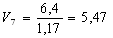
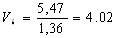
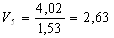
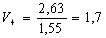
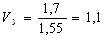
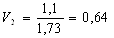
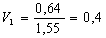
С учетом найденных скоростей прокатки найдем по формуле (6) частоту вращения валков:

об/мин; об/мин;

об/мин; об/мин;

об/мин; об/мин;

об/мин; об/мин.

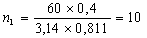
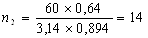
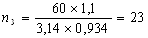
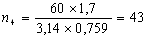
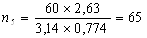
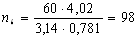
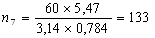
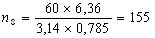
Определим абсолютное изменение приведенной высоты по формуле (8):

ΔН_с1 = (263 – 189) = 74 мм; ΔН_с2 = (189 – 106) = 83 мм;

ΔН_с3 = (106 – 66) = 40 мм; ΔН_с4 = (66 – 41) = 25 мм;

ΔН_с5 = (41 – 26) = 15 мм; ΔН_с6 = (26 – 19) = 7 мм;

ΔН_с7 = (19 – 16) = 3 мм; ΔН_с8 = (16 – 15) = 1 мм.

Определим среднее значение приведенных высот в калибре по формуле (9):

Н_ср1 = (263 + 189)/2 = 226 мм; Н_ср2 = (189+ 106) /2= 148 мм;

Н_ср3 = (106 + 66) /2= 86 мм; Н_ср4 = (66 + 41) /2= 53,5 мм;

Н_ср5 = (41 + 26) /2= 33,5 мм; Н_ср6 = (26 + 19) /2 = 22,5 мм;

Н_ср7 = (19 + 16) /2= 17,5 мм; Н_ср8 = (16 + 15) /2= 15,5 мм.

Найдем по формуле (10) относительное обжатие в каждой клети:

; ; ; ; ;

; ; .

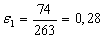
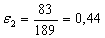
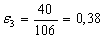
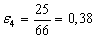
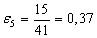
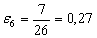
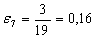
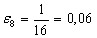
В каждом калибре определим по формуле (11) скорость деформации металла:

Рассчитаем по формуле (12) длину очага деформации:

мм; мм;

мм; мм;

мм; мм;

мм; мм.

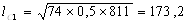
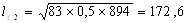
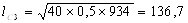
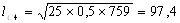
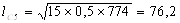
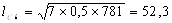
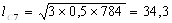
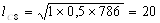
Рассчитаем контактную площадь прокатки по формуле (13):

F₁ = 0,5×(300 + 307)×173,2 = 52566,2 мм 2 ;

F₂ = 0,5×(307 + 316,8)×172,6 = 51833 мм 2 ;

F₃ = 0,5×(316,8 + 328)×136,7 = 44072,1 мм 2 ;

F₄ = 0,5×(328 + 338)×97,4 = 32434,2 мм 2 ;

F₅ = 0,5×(338 + 348)×76,2 = 26136,6 мм 2 ;

F₆ = 0,5×(348 + 355,2)×52,3 = 18388,68 мм 2 ;

F₇ = 0,5×(355,2 + 358)×34,3 = 12231,38 мм 2 ;

Принимая начальную длину двутавровой балки 5 метров, найдем по формуле (14) длины раската по проходам:

L₁ = 5×1,55 = 7,75 мм; L₂ = 7,75×1,73 = 13,4 мм; L₃ = 13,4×1,55 = 20,7 мм;

L₄ = 20,7×1,55 = 32 мм; L₅ = 32×1,53 = 49,3 мм; L₆ = 49,3×1,36 = 67 мм;

L₇ = 67×1,17 = 78 мм; L₈ = 78×1,08 = 84 мм.

В дальнейшем расчет будем вести по каждой клети в отдельности по ходу прокатки, так как для расчета изменения температуры металла по проходам нам необходимо знать температуру металла в предыдущей клети.

Выполним расчет для первой клети.

σ₁ = 82,32×0,78×1,39×0,7 = 62,47 МПа.

Определяем температуру раската перед входом во вторую клеть.

Рассчитаем по формуле (16) время охлаждения раската:

сек.

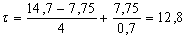
Найдем по формуле (17) повышение температуры металла вследствие перехода механической энергии деформации в теплоту:

Δt_д = 0,183×62,47×ln 1,36 = 3,5 0 C.

Рассчитаем периметр поперечного сечения раската после прохода по формуле (18):

П₁ = 2×(189 + 307) = 992 мм.

Определим изменение температуры раската за время прокатки в калибре и перемещения к следующему калибру по формуле (19):

0 С.

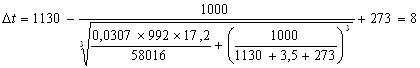
Найдем по формуле (20) температура металла перед заходом в следующую клеть:

t₂ = 1130 – 8 = 1122 0 С.

Аналогично выполним расчет для всех последующих калибров.

По формуле (24) найдем коэффициент внешнего трения для каждого калибра:

μ₁ = 0,55 – 0,00024×1122 = 0,281; μ₂ = 0,55 – 0,00024×1097 = 0,287;

μ₃ = 0,55 – 0,00024×1069 = 0,2934; μ₄ = 0,55 – 0,00024×1047 = 0,299;

μ₅ = 0,55 – 0,00024×1022 = 0,305; μ₆ = 0,55 – 0,00024×924 = 0,328;

μ₇ = 0,55 – 0,00024×905 = 0,333; μ₈ = 0,55 – 0,00024×882 = 0,338.

Найдем по формуле (23) коэффициент, учитывающий влияние контактного трения на форму очага деформации в каждом калибре:

; ;

; ;

; ;

; .

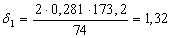
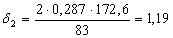
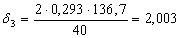
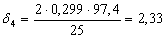
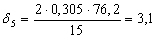
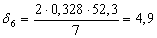
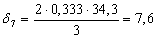
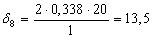
Найдем по формуле (22) коэффициент напряженного состояния:

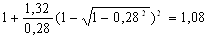
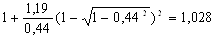
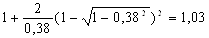
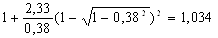
n_σ1 = ; n_σ2 = ;

n_σ3 = ; n_σ4 = ;

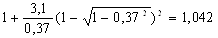
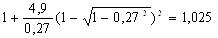
n_σ5 = ; n_σ6 = ;

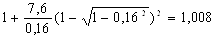
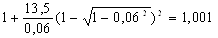
n_σ7 = ; n_σ8 = .

Определим по формуле (25) значение коэффициента, учитывающего влияние внешних зон по отношению к геометрическому очагу деформации:

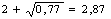
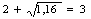
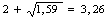
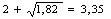
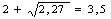
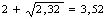
n_ж1 = ; n_ж2 = ; n_ж3 = ;

n_ж4 = ; n_ж5 = ; n_ж6 =;

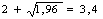
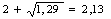
n_ж7 = ; n_ж8 = .

Найдем коэффициент формы профиля используя формулу (26):

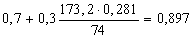
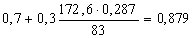
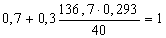
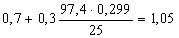
n_ф1 = ; n_ф2 = ;

n_ф3 = ; n_ф4 = ;

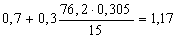
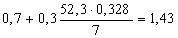
n_ф5 = ; n_ф6 = ;

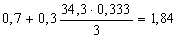
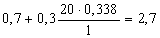
n_ф7 = ; n_ф8 = .

Рассчитаем контактное давление прокатки по формуле (21):

р₁ = 1,08×1,08×1,12×0,897×62,47 = 73,2 МПа;

р₂ = 1,08×1,028×0,92×0,879×77 = 69,13 МПа;

р₃ = 1,08×1,03×0,74×1 ×100 = 82,32 МПа;

р₄ = 1,08×1,034×0,65×1,05×115 = 87,65 МПа;

р₅ = 1,08×1,042×0,49×1,17×115,3 = 74,39 МПа;

р₆ = 1,08×1,025×0,47×1,43×153 = 113,83 МПа;

р₇ = 1,08×1,008×0,6×1,84×118,5 = 142,4 МПа;

р₈ = 1,08×1,001×0,86×2,7×133,7 = 335,6 МПа.

Рассчитаем усилия прокатки по формуле (27):

Определим по формуле (28) коэффициент плеча приложения усилия прокатки:

φ_п1 = 5,85 – 11×0,77 + 7,35×0,77 2 – 1,58×0,77 3 = 0,989;

φ_п2 = 5,85 – 11×1,16 + 7,35×1,16 2 – 1,58×1,16 3 = 0,514;

φ_п3 = 5,85 – 11×1,59 + 7,35×1,59 2 – 1,58×1,59 3 = 0,59;

φ_п4 = 5,85 – 11×1,82 + 7,35×1,82 2 – 1,58×1,82 3 = 0,65;

φ_п5 = 5,85 – 11×2,27 + 7,35×2,27 2 – 1,58×2,27 3 = 0,272;

φ_п6 = 5,85 – 11×2,32 + 7,35×2,32 2 – 1,58×2,32 3 = 0,161;

φ_п7 = 5,85 – 11×1,96 + 7,35×1,96 2 – 1,58×1,96 3 = 0,63;

φ_п8 = 5,85 – 11×1,29 + 7,35×1,29 2 – 1,58×1,29 3 = 0,5.

Все клети стана имеют индивидуальный привод. Найдем по формуле (30) коэффициент загрузки электродвигателей стана по усилию прокатки:

Мн; Мн; Мн;

Мн; Мн; Мн;

Мн; Мн.

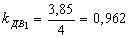
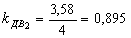
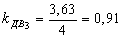
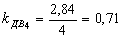
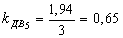
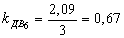
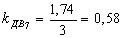
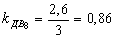
По формуле (33) определим производительность стана в час:

т/ч.

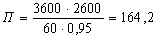
Результаты расчета основных технологических параметров прокатки приведены в таблице 8.1.

Таблица 8.1. Результаты расчета основных технологических параметров прокатке двутавровой балки №36

11898110,410112262,471,080,89773,252566,23,850,9622,8721069940,64141097771,0280,87969,13518333,580,89533669341,1231069100,81,03182,3244072,13,630,913,264417591,7431047115,81,0341,0587,6532434,22,840,713,355267742,63651022115,31,0421,1774,3926136,61,940,653,56197814,0298924153,31,0251,43113,8318388,72,090,673,527167845,47133905118,51,0081,84142,412231,41,740,583,48157856,36155882133,71,0012,7335,678002,60,862,13

Таким образом, рассчитанная калибровка валков позволяет рационально использовать скоростные и энергосиловые возможности стана. Расчет показывает, что прокатка заданной двутавровой балки №36 на данном стане возможна, т.е. рассчитанные усилия прокатки не приведут к повышенному износу валков, они меньше предельного усилия. Коэффициент загрузки электродвигателей стана по усилию прокатки меньше допустимого.

В процессе выполнения данной курсовой работы был изучен двутавровый профиль со всеми его разновидностями. Для данного расчета был выбран полунепрерывный стан 800 Нижнетагильского металлургического комбината. Так же приведена схема расположения основного технологического оборудования, основных профилей сортамента стана, печей, рабочих клетей, прокатных валков и двигателей прокатного стана 800 НТМК. Приведена технико-экономические показатели работы стана. При нахождении основных размеров калибров учитывалась температура прокатываемой стали. Изучены способы прокатки и калибровки профиля в зависимости от вида и размеров профиля, а также конструкции прокатных станов применяющие различные способы прокатки балок. Получены навыки расчета калибровки валков для проката двутавровой балки. Нами был выполнен расчет калибровки двутавровой балки №36 по ГОСТ 8239–72, пользуясь методом А.П. Чекмарева, а также найдены основные технологические параметры прокатки. Было выбрано необходимое число проходов для прокатки двутавровой балки №36 равное восьми калибрам. В расчете энергосиловых параметров прокатки рассчитанная калибровка валков позволяет рационально использовать скоростные и энергосиловые возможности стана. Нами была рассчитана производительность стана по выбранному режиму прокатки составила 164,2 т/ч. В расчете учитывалась марка стали из которой изготавливают данный профиль. Сталь – углеродистая качественная конструкционная 20КП по ГОСТ 1050–74. Был произведен расчет технологический параметров. Расчет показывает, что прокатка двутавровой балки №36 на полунепрерывном стане 800 Нижнетагильского металлургического комбината возможна выполнением оптимизации.

Список используемых источников

1. Чекмарев А.П., Мутьев М.С., Машковец Р.А. Калибровка прокатных валков. – М.: Металлургия, 1971, 512 с.

2. Королев А.А. Прокатные станы и оборудование прокатных цехов. Атлас. Том 2. – М.: Металлургия, 1981, 208 с.

3. Смирнов В.К., Шилов В.А., Инатович Ю.В. Калибровка прокатных валков. – М.: Металлургия, 1987, 368 с.

4. Диомидов Б.Б., Литовченко Н.В. Калибровка валков сортовых станов. Металлургиздат, 1963, 360 с.

5. Протасов А.А. Сборник задач по технологии горячей и холодной прокатки стали и сплавов. – Металлургия, 1972, 320 с.

6. Справочник металлиста. – М.: Машиностроение. Т.3, 1976, 125 с.

7. Полухин П.И. Прокатка и калибровка двутавровых балок. М.: Металлургизд, 1956, 175 с.

8. Бахтинов Б.П., Штернов М.М. Калибровка балок и швеллеров. М.: Металлургизд, 1950, 170 с.

Источник