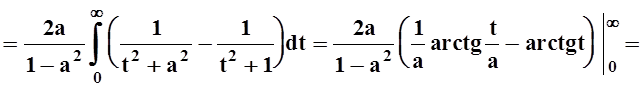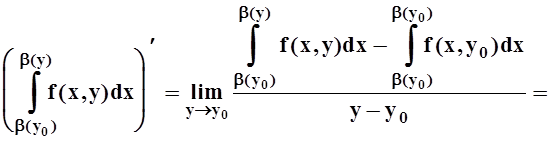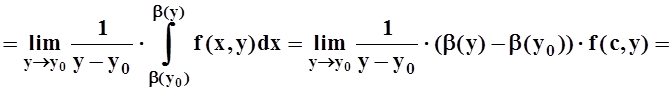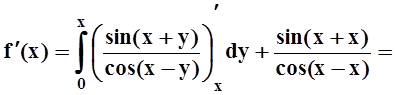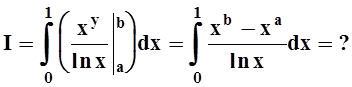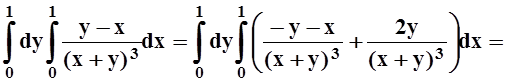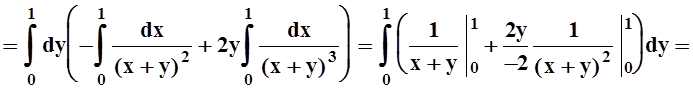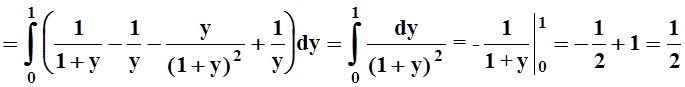С помощью дифференцирования по параметру вычислить интеграл

Дифференцирование по параметру иногда можно применять для вычисления интегралов.

Пример 5. Вычислить 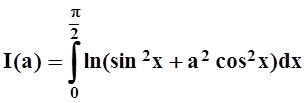при a > 1.

Решение. Найдём производную интеграла по параметру а. Легко проверить, что требования теоремы 4 соблюдены, поэтому

.

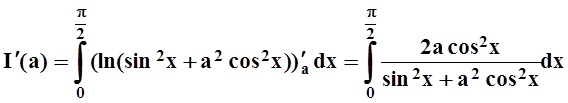
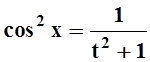
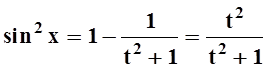
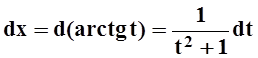
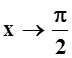
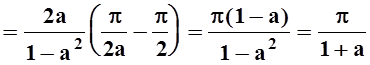
Применим подстановку t= tgx. Тогда , , . Если х®0,то t®0, если , то t®¥. Продолжаем вычисление:

.

Теперь, вычисляя интеграл, получим:

.

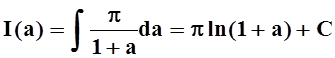
Константу С найти легко, так как

.

.

Научимся теперь вычислять производные в случае, если от параметра зависит не только подинтегральная функция, но и пределы интегрирования.

Теорема 5. Пусть f(x,y), непрерывны в прямоугольнике D= [a,b]´[c,d]; пусть функции a(y), b(y) при yÎ[c, d] дифференцируемы, причём a £a(y) £ b, a£b(y)£b. Тогда

.

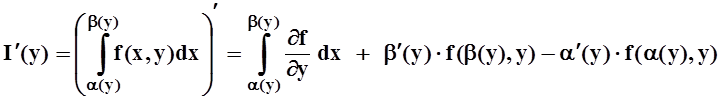
Доказательство. Возьмём произвольную точку y₀Î[c, d] и вычислим по определению: . Но прежде запишем, пользуясь аддитивностью интеграла:

.

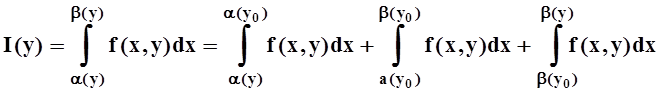
Производная 2–го слагаемого вычисляется по теореме 4:

.

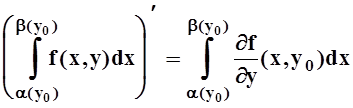
Найдём производную 3–го слагаемого:

.

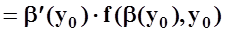
Мы воспользовались теоремой о среднем для определённого интеграла, а затем – непрерывностью f(x,y) и дифференцируемостью b(y). В точности так же вычисляется и производная 1–го слагаемого:

.

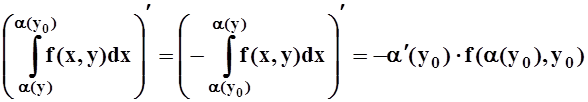
Складывая все 3 слагаемые, получим требуемую формулу (в произвольной точке y₀Î[c, d]).

Пример 6. Найти производную функции

Решение. Здесь требуется дифференцировать интеграл по параметру х. Действуем по формуле теоремы 5:

.

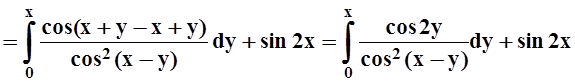
16.1.3 Интегрирование по параметру.

Теорема 6. Пусть f(x,y) непрерывна в прямоугольнике D= [a,b]´ [c,d]. Рассмотрим . Тогда

.

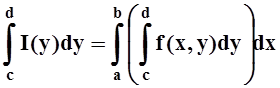
Или, что то же самое,

.

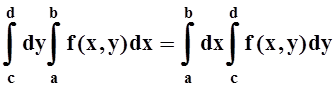
Доказательство. Докажем более общее соотношение. Пусть t –произвольная точка отрезка [c, d]. Докажем, что

. (*)

Найдём производную по t от каждой части этого равенства. Применяя теорему 5 (или давно известную нам теорему об интеграле с переменным верхним пределом), получим:

.

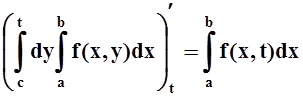
В правой части равенства (*) – интеграл, зависящий от параметра t. Дифференцируем его, применяя теорему 4:

.

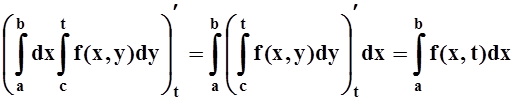
Одинаковые результаты говорят о том, что функции в левой и правой частях равенства (*) отличаются лишь на константу: 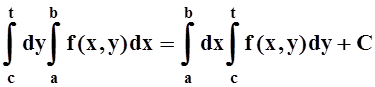. Это верно «tÎ[c, d]. В частности, при t= c получим: 0= 0 + С, т.е. С= 0 и равенство доказано. Если применить его при t= d, получим утверждение теоремы.

Пример 7. Вычислить интеграл .

Решение. Интегрирование в указанном порядке затруднительно:

Пользуясь теоремой 6, изменим порядок интегрирования.

.

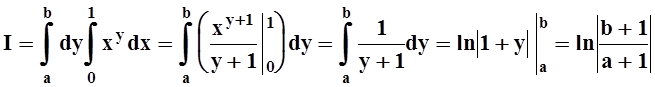
Интеграл вычислен. Попутно получено соотношение:

.

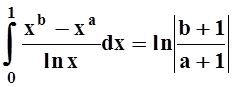
Приведём пример, показывающий, что при нарушении непрерывности подинтегральной функции изменение порядка интегрирования может привести к другому результату.

Пример 8. Вычислим интеграл:

При вычислении в другом порядке можно заметить, что если сменить знак подинтегральной функции, то получится уже рассмотренный интеграл:

.

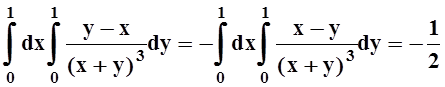
Разные ответы – из–за того, что подинтегральная функция в точке (0, 0) имеет разрыв.

16.2 Несобственные интегралы с параметром

Перейдём к изучению несобственных интегралов, зависящих от параметра. Наиболее простая запись такого интеграла – это по–прежнему

, но здесь либо b = ¥, либо функция f(x, y) не ограничена в окрестности точки x = b. Для краткости будем говорить, что интеграл имеет особенность в точке x = b. Переменная y принимает значения на отрезке [c, d] (или на неограниченном промежутке, например, [c,¥)).

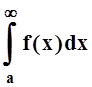
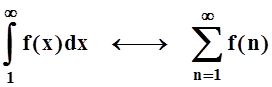
При изучении несобственных интегралов вида мы обращали внимание на их аналогию с числовыми рядами. Аналогичны не только термины («сходится», «расходится»), но и существо дела. Например, признаки сравнения для несобственных интегралов и числовых рядов формулируются и доказываются одинаково. В интегральном признаке сходимости числовых рядов прямо сопоставляются несобственный интеграл и числовой ряд:

.

Похожая ситуация имеет место и для несобственных интегралов, зависящих от параметра. Но здесь аналогия устанавливается не с числовыми, а с функциональными рядами:

.

Функциональные ряды мы изучали в 14 модуле, теперь можно сравнить и сопоставить их свойства со свойствами несобственных интегралов с параметром.

Важным в теории функциональных рядов было понятие равномерной сходимости. Оказывается, и здесь оно играет ключевую роль.

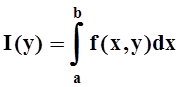
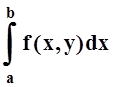
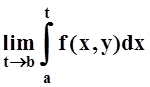
Дадим определения. Интеграл с особенностью в точке x = b сходится на [c, d], если «yÎ[c,d] интеграл сходится, т.е. существует конечный .

Будем говорить, что 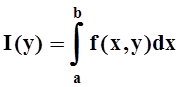сходится равномерно на [c, d], если

Источник

Интегралы, зависящие от параметра

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Собственные интегралы, зависящие от параметра 1.1. Понятие интеграла, зависящего от параметра, и его непрерывность Пусть в прямоугольнике определена функция двух переменных f(x, у) (рис. 1). Предположим, что при любом фиксированном значении у е [с, d] существует интеграл ь Ясно, что этот интеграл является функцией переменного у, Интеграл (1) называется интегралом, зависящим от параметра у. Имеет место следующая теорема о непрерывности интеграла, зависящего от параметра.

Теорема 1:

Если функция /(х, у) непрерывна в прямоугольнике П, то функция /(у), определенная соотношением (1), непрерывна на отрезке [с, d\. Из формулы (1) вытекает, что приращение ) функции /(у), соответствующее приращению аргумента Ду, можно оценить так: По условию теоремы функция f у) непрерывна в замкнутом прямоугольнике П, а значит, fy) равномерно непрерывна в этом прямоугольнике.

Возможно вам будут полезны данные страницы:

Интеграл (1) называется абсолютно сходящимся на отрезке [с, d\, если сходится интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра 2.2. Равномерная сходимость несобственного интеграла. Критерий Коши Определение 2.

Несобственный интеграл

Несобственный интеграл (1) называется равномерно сходящимся по параметру у наотрезке [с, d), если он сходится наэтомотрезкеи для любого е > 0 можно указать такое А ^ а, зависящее только от е, что для всех В > А и для всех у из отрезка [с, d\ выполняется неравенство Имеетместоследующий критерий Коши равномерной сходимости несобстве нных интегралов, зависящих от параметра.

Теорема 4. Для того, чтобы несобственный интеграл (1) равномерно сходился по параметру у на отрезке [с, d\, необходимо и достаточно, чтобы для любого е > 0 можно было указать число А ^ а, зависящее только от е и такое, что для любых В и С, больших А, и для всех у из отрезка [с, d] выполнялось неравенство Справедливость этого критерия вытекает непосредственно из определения равномерной сходимости. Сформулируем достаточный признак равномерной сходимости несобственных интегралов, зависящих от параметра. Теорема 5 (признак Вейерштрасса).

Пусть функция /(х, у) определена в пыупыосе Поо и для каждого у € | с, d] интегрируема по х на любом отрезке [а, Л]. Пусть, кроме того, для всех точек полуполосы П^ выполняется неравенство Тогда из сходимости интеграла f g(x) dx вытекает равномерная сходимость по у наот- резке [с, d] несобственного интегрша В силу критерия Коши сходимости интеграла от функции для любого е > О можно указать число А ^ а такое, что при всех С > В ^ А выполняется неравенство Используя неравенство (4), отсюда получим, что для всех у из отрезка Тем самым, критерий Коши равномерной сходимости интеграла выполнен. Цитр 1.

Иссладова тъ на равномерную сходимость несобственный иктграл где я — параметр, Так как при любом произвольные вещественные числа, выполняется неравенство и интеграл сходится, то по признаку Вейерштрасса интеграл (5) равномерно сходится для всех 2.3. Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра Свойство 1. Непрерывность несобственного интеграла по параметру. Если функция непрерывна в области Поо и интеграл сходится равномернопо у наотрезкс (с, dj,то функция 1(у) непрерывна на Свойство 2. Интегрируемость несобственно го интеграла по параметру.

В самом деле, при любом в, и откуда по признаку Вейерштрасса следует равномерная сходимость интеграла (9). Обозначая подынтегральную функцию интеграла (5) через замечаем, что — подынтегральная функция равномерно сходящегося интеграла (9). Используя свойство дифференцируемое™ несобственного интеграла по параметру, получим Так как 1($) = (в этом легко убедиться путем интегрирования по частям), то Отсюда Пример 3.

Покажем сначала, что несобственный интеграл Собственные интегралы зависящие от параметра Дифференцирование интеграла no параметру Интегрирование интеграла по параметру Понятие несобственного интеграла первого рода, зависящего от параметра Равномерная сходимость несобственного интеграла Критерий Коши Свойства равномерно сходящихся несобственных интегралов, зависящих от параметра зависящий от параметра у, сходится равномерно на отрезке (а, 6).

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Интегралы, зависящие от параметра. Несобственные интегралы с параметром

Страницы работы

Содержание работы

16 Интегралы, зависящие от параметра

Пусть f(x,y) – функция двух переменных, определённая на прямоугольнике

Если для любого yÎ[c, d] существует интеграл 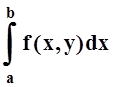, то этот интеграл является функцией от переменной y (которая и называется здесь параметром):

.

Таким образом, мы получаем новый способ задания функции – в виде интеграла, зависящего от параметра.

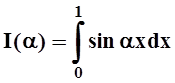
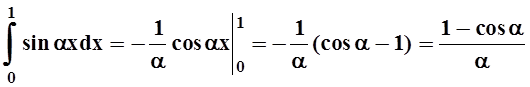
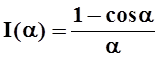
Пример 1. Рассмотрим функцию . В этом примере интеграл легко вычислить: . Значит, I(a) можно задать и обычным способом: .

Однако часто встречаются интегралы, которые не выражаются через элементарные функции. Тогда приходится работать с функцией, заданной в виде интеграла с параметром. Значит, нужно научиться работать с такими функциями – в частности, знать правила их дифференцирования и интегрирования.

Возможна и более сложная ситуация, когда от параметра зависит не только подинтегральная функция, но и пределы интегрирования: .

16.1 Основные теоремы

16.1.1 Предельный переход под знаком интеграла.

Теорема 1 (о непрерывности интеграла с параметром). Если функция f(x,y) непрерывна на прямоугольнике D= [a, b] ´ [c, d], то функция 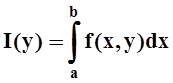непрерывна на отрезке [c, d].

Доказательство. По теореме Кантора, непрерывная на компактном множестве Dфункция является равномерно непрерывной, т.е.

Источник

Дифференцирование интеграла по параметру

Дифференцирование интеграла по параметру

точно так же, как она доказала теорему 5 в n°269. Пусть функция теоремы 6 f (x,y)определена x для x^a

и y для[b]и непрерывна.,&>, Людмила Фирмаль

Является смежным с дифференциалом f’u (x, y)обеих переменных для указанного значения.160ч. По интегральному параметру XVIII[307]

Кроме того, для всех y из[s, y] Интеграл (1) и Интеграл с x o d и t s I И §ГУ (х, у) АХ(8) Но Она не только существует, но и сходится p a с n O m e R n o для y на том же интервале. Тогда для любого y из[s, y\

Таким образом, та же производная имеет Интеграл(1) в конечной Людмила Фирмаль

части уравнения и отличается от интеграла слева только константой. Теорема доказана

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Собственные интегралы, зависящие от параметра

Определение собственного интеграла, зависящего от параметра.

Обычно \(Y\) является числовым множеством или множеством в \(\boldsymbol^\). Например,
$$
J_<0>(x) = \frac<1> <\pi>\int\limits_<0>^ <\pi>\cos (x \cos \varphi)\ d\varphi\label
$$
есть собственный интеграл, зависящий от параметра \(x \in (-\infty, +\infty)\).

Свойства собственного интеграла, зависящего от параметра.

(Теорема о непрерывной зависимости собственного интеграла от параметра).

Если функция \(f(x, y)\) непрерывна в прямоугольнике \(K = \<(x, y): a \leq x \leq b, c \leq y \leq d\>\), то интеграл \eqref есть непрерывная функция параметра \(y\) на \([c, d]\).

Доказательство этой теоремы приведено мы приводили ранее.

(Теорема о перестановке порядка интегрирования).

\(\circ\) Каждый из повторных интегралов в формуле \eqref равен двойному интегралу от функции \(f(x, y)\) по прямоугольнику \(K\) (соответствующую теорему мы доказывали). \(\bullet\)

(Теорема о дифференцировании собственного интеграла по параметру).

Пусть функция \(f(x, y)\) непрерывна в прямоугольнике \(K = \<(x, y): a \leq x \leq b, c \leq y \leq d\>\) и имеет непрерывную частную производную \(\displaystyle\frac<\partial f(x, y)><\partial y>\) в области \(G\) такой, что \(K \subset G\).

Левая часть равенства \eqref может быть записана как \(\displaystyle\int\limits_^ \varphi(\eta) d\eta\). Так как функция \(\varphi(\eta)\) непрерывна на отрезке \([c, d]\), то
$$
\frac \int\limits_^ \varphi(\eta)\ d\eta = \varphi(y) = \int\limits_^ \frac<\partial f><\partial y>(x, y)\ dx.\nonumber
$$

Теоремы 1-3 остаются справедливыми и при замене функции \(f(x, y)\) на функцию \(\psi(x)f(x, y)\), где функция \(\psi(x)\) интегрируема на отрезке \([a, b]\).

Источник