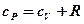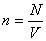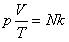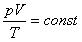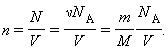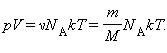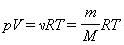Состояние идеального газа определяется значениями параметров т0 р0 v0 где т термодинамическая

Состояние идеального газа определяется значениями параметров т0 р0 v0 где т термодинамическая

Файл: Тест.docx

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлена: 31.01.2019

Просмотров: 8567

Скачиваний: 82

На рисунке изображен цикл Карно в координатах (T,S), где S-энтропия. Адиабатное сжатие происходит на этапе …

Процессы 2-3 и 4-1 являются адиабатными. Адиабатное сжатие происходит на этапе возрастания температуры, т.е. на участке 4 – 1.

Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…

1: адиабатным сжатием*

2: изохорным нагреванием

3: изобарным расширением

4: изотермическим расширением

Поскольку в процессе 1-2 не происходит изменения энтропии, то процесс является адиабатным. Т.к. температура Т увеличивается, то происходит процесс адиабатного сжатия.

Процесс, изображенный на рисунке в координатах (T,S), где S-энтропия, является…

1: адиабатным расширением*

2: изохорным охлаждением

3: изобарным сжатием

4: изотермическим сжатием

Поскольку в процессе 1-2 не происходит изменения энтропии, то процесс является адиабатным. Т.к. температура Т уменьшается, то происходит процесс адиабатного расширения.

Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С ₁ и С ₂ соответственно.

Молярные теплоемкости гелия в процессах 1-2 и 1-3 равны С ₁ и С ₂ соответственно.

Среди приведённых формул к изотермическому процессу имеют отношение

_{– адиабатный процесс; – изобарный процесс; – адиабатный процесс.}

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы соотношения…

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного сжатия газа справедливы соотношения…

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного сжатия газа справедливы соотношения…

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для изохорного охлаждения газа справедливы соотношения…

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для изобарного охлаждения газа справедливы соотношения…

Внутренняя энергия уменьшается за счёт того, что над газом совершается работа и газ отдаёт тепло окружающей среде.

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для изотермического сжатия газа справедливы соотношения…

При совершении работы внешними силами газ отдаёт тепло окружающей среде.

Если – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для изобарного нагревания газа справедливы соотношения…

Источник

ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ

ЗАДАНИЕ № 4

Укажите, в какой из приведенных единиц измерения не может быть выражена постоянная Больцмана.

ВАРИАНТЫ ОТВЕТОВ:

ЗАДАНИЕ № 5

ВАРИАНТЫ ОТВЕТОВ:

ЗАДАНИЕ № 6

В классическом описании газа из N двухатомных молекул используются две возможные модели для молекулы:

Жесткая гантель Упpугая гантель
Какое из следующих утвеpждений веpно для этого газа?

ВАРИАНТЫ ОТВЕТОВ:

1. Удельная теплоемкость для втоpой модели меньше, чем для пеpвой модели.

2. Модель 1 всегда коppектна.

3. Модель 2 всегда коppектна.

5. Выбоp модели зависит от темпеpатуpы.

Указания к заданиям № 4 – 6

Средняя кинетическая энергия молекулы идеального газа при температуре Т равна 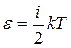. Здесь i = п_п + п_вр + 2п_к , где п_п , п_вр и п_к – число степеней

свободы поступательного, вращательного и колебательного движений молекулы.

Молярная теплоемкость при постоянном объеме C_v и при постоянном давлении C_p: ,

где DU – изменение внутренней энергии; A – работа над внешними телами;

n – число молей; DT – изменение температуры.

( i – число степеней свободы молекулы).

– уравнение Майера. R=kN_A (N_A – число Авогадро).

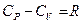
Для многоатомных молекул число степеней свободы, проявляющихся в теплоемкости газа, зависит от температуры. С повышением температуры, кроме степеней свободы поступательного движения, увеличивается роль степеней свободы вращательного и колебательного движений молекулы.

ЗАДАНИЕ № 7

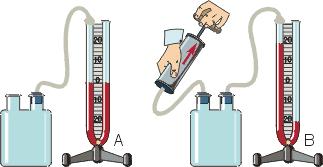
Состояние идеального газа определяется значениями параметров: T₀, p₀, V₀,

где Т – термодинамическая температура, р – давление, V – объем газа. Определенное количество газа перевели из состояния (р₀, V₀ ) в состояние

ВАРИАНТЫ ОТВЕТОВ:

1) не изменилась; 2) уменьшилась;3) увеличилась.

Уравнение Клапейрона-Менделеева: .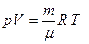

Изменение внутренней энергии идеального газа: .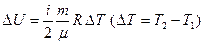

ЗАДАНИЕ № 8

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы соотношения.

ВАРИАНТЫ ОТВЕТОВ:

Q – количество теплоты, сообщаемое газу, то для изотермического сжатия газа справедливы соотношения.

ВАРИАНТЫ ОТВЕТОВ:

ЗАДАНИЕ № 11

Если DU – изменение внутренней энергии идеального газа, А – работа газа,

Q – количество теплоты, сообщаемое газу, то для изохорного нагревания газа справедливы соотношения.

ВАРИАНТЫ ОТВЕТОВ:

Уравнение адиабатного (Q=0) процесса в координатах (V, T): .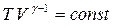

Работа при адиабатном процессе: .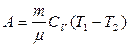

Уравнение изотермического (T=const) процесса: .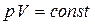

Работа при изотермическом процессе: .

Уравнение изобарного (p=const) процесса: .

Работа при изобарном процессе: .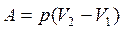

Уравнение изохорного (V=const) процесса: .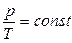

Работа при изохорном процессе: .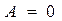

Изменение внутренней энергии: .

Первое начало термодинамики: .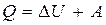

Источник

Число степеней свободы молекулы это

а) число атомов в молекуле;

б) число параметров, задающих микросостояние системы;

+ в) число независимых координат, определяющих положение тела в пространстве;

г) число различных микросостояний, посредством которых осуществляется данное макросостояние.

65.Можно ли говорить о температуре одной молекулы?

а) можно, так как молекула обладает кинетической энергией;

+ б) нельзя, так как температура — параметр статистический;

в) можно, так как скорость молекулы зависит от температуры;

г) нельзя, так как зависимость между скоростью молекулы и температурой нелинейная.

66.Какой параметр х идеального газа можно определить по формуле 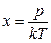, где р – давление газа, k – постоянная Больцмана, Т – абсолютная температура идеального газа?

б) среднюю квадратичную скорость молекул;

+ г) концентрацию молекул.

67. КПД теплового двигателя 50%, а температура рабочего тела в нагревателе 500 К. Температура холодильника

68. Состояние идеального газа определяется значениями параметров: T₀, p₀, V₀, где Т – термодинамическая температура, p – давление, V – объем газа. Определенное количество газа перевели из состояния в состояние . При этом его внутренняя энергия…

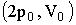
69. Если 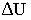– изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы соотношения…

+а) ;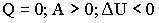

б) ;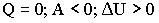

в) ;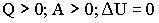

г) .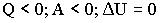

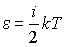
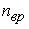
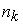
70. Средняя кинетическая энергия молекулы идеального газа при температуре T равна . Здесь , где , и – число степеней свободы поступательного, вращательного и колебательного движений молекулы. Для гелия (He) число i равно …

71. Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла…

72. Температура идеального газа по шкале Кельвина возросла в два раза. Средняя кинетическая энергия молекул газа

а) возросла в 1,4 раза;

+ б) возросла в 2 раза;

в) возросла в 4 раза;

73. Согласно закону о равномерном распределении энергии по степеням свободы молекулы на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная:

+а) ;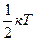

б) ;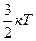

74. Укажите правильный порядок расположения равенств: , ,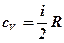

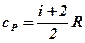
+а) молярная теплоемкость при V=const, молярная теплоемкость при P=const, уравнение Майера;

б) молярная теплоемкость при P=const, молярная теплоемкость при V=const, уравнение Майера;

в) уравнение Майера, молярная теплоемкость при V=const, молярная теплоемкость при P=const;;

г) молярная теплоемкость при V=const, уравнение Майера, молярная теплоемкость при P=const.

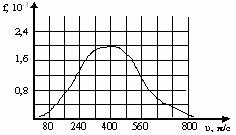
75. На рисунке приведена функция распределения молекул азота (μ = 0,028 кг/моль). Какое значения имеет наиболее вероятная скорость движения молекул газа?

76. Средняя арифметическая скорость движения:

+б) = ;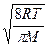

в) = ;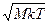

+г) _вер

86. На VP-диаграмме изображено изменение состояния идеального газа, при котором газ отдал количество теплоты, равное 800 Дж. 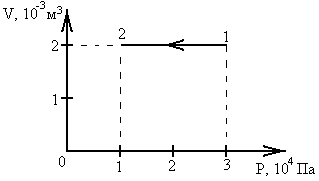Внутренняя энергия газа:

б) увеличилась на 800 Дж;

+ в) уменьшилась на 800 Дж;

г) уменьшилась на 40 Дж.

87. В результате охлаждения идеального газа его давление уменьшилось в 4 раза, а концентрация молекул не изменилась. Средняя кинетическая энергия теплового движения молекул газа при этом:

а) уменьшилась в 16 раз;

+ б) уменьшилась в 4 раза;

в) уменьшилась в 2 раза;

88. На VT–диаграмме изображен циклический процесс изменения состояния идеального газа. 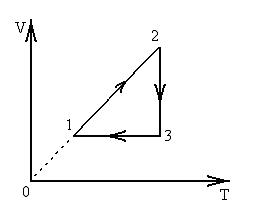На каком участке внутренняя энергия газа увеличивается?

89. На РТ-диаграмме изображено изменение состояния идеального газа. На каком участке внутренняя энергия газа уменьшается?

90. На диаграмме изображено изменение состояния идеального газа. 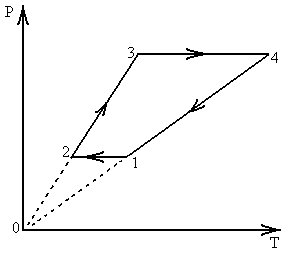На каком участке работа не совершается?

91. При любом циклическом процессе:

а) работа, совершаемая газом за цикл, равна нулю;

б) количество теплоты, получаемое газом за цикл, равно нулю;

в) изменение объема газа за цикл не равно нулю;

+ г) изменение внутренней энергии газа за цикл равно нулю.

92. Какие из агрегатных состояний вещества охватывает изотерма Ван-дер-Ваальса, построенная для температуры ниже критической?

г) газ, жидкость и твердое тело.

93. Какие из агрегатных состояний вещества охватывает изотерма Ван-дер-Ваальса, построенная для температуры выше критической?

г) газ, жидкость и твердое тело.

94. В процессе плавления твердого тела подводимое тепло идет на разрыв межатомных (межмолекулярных) связей и разрушение кристаллической решетки. Внутренняя энергия тела при этом:

г) иногда увеличивается, иногда уменьшается.

95. Назовите верную формулировку второго закона термодинамики:

а) самопроизвольные процессы всегда сопровождаются убыванием энергии;

б) энтропия открытой системы либо уменьшается (в необратимых процессах), либо остается постоянной (в обратимых процессах);

в) ни при каких условиях невозможно увеличение энтропии термодинамической системы;

+г) энтропия изолированной системы либо возрастает (в необратимых процессах), либо остаётся неизменной (в необратимых процессах).

а) физическая величина, определяющая направление протекания процессов в природе;

б) функция состояния, полным дифференциалом которой в обратимых процессах является приведенное количество теплоты δQ/Т;

в) физическая величина, характеризующая вероятность состояния системы;

+г) функция процесса, полным дифференциалом которой в обратимых процессах является приведенное количество теплоты δQ/Т.

97. Какое из перечисленных утверждений ошибочно:

а) энтропия системы равна сумме энтропий тел, входящих в эту систему;

+б) энтропия системы зависит от процесса, в результате которого система пришла в данное состояние;

в) энтропия замкнутой системы может оставаться постоянной;

г) энтропия зависит от параметров состояния системы и не зависит от пути, по которому система пришла в это состояние.

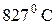
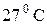
98. Вычислите максимальное значение КПД, которое может иметь тепловая машина с температурой нагревателя и температурой холодильника :

а) ;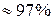

б) ;

в) ;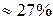

+г) .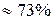

99. Температура нагревателя тепловой машины, совершающей цикл Карно, равна 400 К, а холодильника 300 К. Термический коэффициент полезного действия машины составляет

100. Чтобы увеличить КПД идеальной тепловой машины, нужно: А. Повысить температуру нагревателя. Б. Понизить температуру холодильника. Какое(ие) из утверждений правильно(ы)?

101. Какое выражение соответствует первому началу термодинамики при изотермическом сжатии идеального газа?

Источник

Как сказал.

Жизнь — как вождение велосипеда. Чтобы сохранить равновесие, ты должен двигаться

Вопросы к экзамену

Для всех групп технического профиля

Список лекций по физике за 1,2 семестр

Урок 15. Лекция 15. Идеальный газ

Как известно, многие вещества в природе могут находиться в трех агрегатных состояниях: твердом, жидком и газообразном.

Учение о свойствах вещества в различных агрегатных состояниях основывается на представлениях об атомно-молекулярном строении материального мира. В основе молекулярно-кинетической теории строения вещества (МКТ) лежат три основных положения:

Значит, агрегатное состояние вещества зависит от взаимного расположения молекул, расстояния между ними, сил взаимодействия между ними и характера их движения.

Сильнее всего проявляется взаимодействие частиц вещества в твердом состоянии. Расстояние между молекулами примерно равно их собственным размерам. Это приводит к достаточно сильному взаимодействию, что практически лишает частицы возможности двигаться: они колеблются около некоторого положения равновесия. Они сохраняют форму и объем.

Свойства жидкостей также объясняются их строением. Частицы вещества в жидкостях взаимодействуют менее интенсивно, чем в твердых телах, и поэтому могут скачками менять свое местоположение – жидкости не сохраняют свою форму – они текучи. Жидкости сохраняют объем.

Газ представляет собой собрание молекул, беспорядочно движущихся по всем направлениям независимо друг от друга. Газы не имеют собственной формы, занимают весь предоставляемый им объем и легко сжимаются.

Модель идеального газа. Связь между давлением и средней кинетической энергией.

Для выяснения закономерностей, которым подчиняется поведение вещества в газообразном состоянии, рассматривается идеализированная модель реальных газов – идеальный газ. Это такой газ, молекулы которого рассматриваются как материальные точки, не взаимодействующие друг с другом на расстоянии, но взаимодействующие друг с другом и со стенками сосуда при столкновениях.

Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало. (Ек>>Ер)

Идеальный газ – это модель, придуманная учеными для познания газов, которые мы наблюдаем в природе реально. Она может описывать не любой газ. Не применима, когда газ сильно сжат, когда газ переходит в жидкое состояние. Реальные газы ведут себя как идеальный, когда среднее расстояние между молекулами во много раз больше их размеров, т.е. при достаточно больших разрежениях.

Свойства идеального газа:

Состояние некоторой массы газообразного вещества характеризуют зависимыми друг от друга физическими величинами, называемыми параметрами состояния. К ним относятся объем V, давление p и температура T.

Давление – физическая величина, равная отношению силы F, действующей на элемент поверхности перпендикулярно к ней, к площади S этого элемента.

До настоящего времени употребляются внесистемные единицы давления:

техническая атмосфера 1 ат = 9,81-104 Па;

физическая атмосфера 1 атм = 1,013-105 Па;

миллиметры ртутного столба 1 мм рт. ст.= 133 Па;

1 атм = = 760 мм рт. ст. = 1013 гПа.

Как возникает давление газа? Каждая молекула газа, ударяясь о стенку сосуда, в котором она находится, в течение малого промежутка времени дей­ствует на стенку с определенной силой. В результате беспорядочных ударов о стенку сила со стороны всех молекул на единицу площади стенки быстро меняется со временем относительно некоторой (средней) величины.

Давление газа возникает в результате беспорядочных ударов молекул о стенки сосуда, в котором находится газ.

Используя модель идеального газа, можно вычислить давление газа на стенку сосуда.

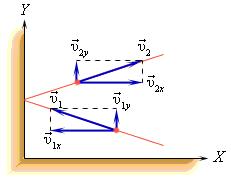
В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υ_x скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υ_y скорости, параллельная стенке, остается неизменной.

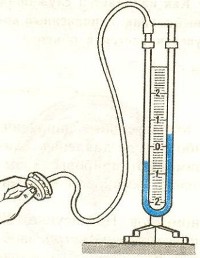
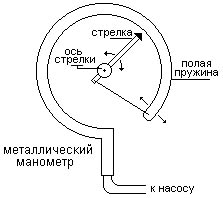
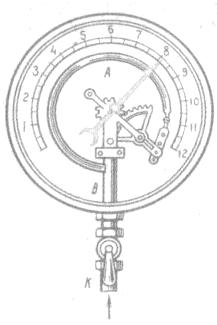
Приборы, измеряющие давление, называют манометрами. Манометры фиксиру­ют среднюю по времени силу давления, приходящуюся на единицу площади его чувствительного элемента (мембраны) или другого приемника давления.

Металлический манометр – для измерения больших давлений.

Основной его частью является изогнутая трубка А, открытый конец которой припаян к трубке В, через которую поступает газ, а закрытый – соединен со стрелкой. Газ поступает через кран и трубку В в трубку А и разгибает её. Свободный конец трубки, перемещаясь, приводит в движение передающий механизм и стрелку. Шкала градуирована в единицах давления.

Основное уравнение молекулярно-кинетической теории идеального газа.

Основное уравнение МКТ: давление идеального газа пропорционально произведению массы молекулы, концентрации молекул и среднему квадрату скорости движения молекул

n = N/V – число молекул в единице объема, или концентрация молекул;

Так как средняя кинетическая энергия поступательного движения молекул E = m₀*v 2 /2, то домножив основное уравнение МКТ на 2, получим p = 2/3· n·(m₀· v 2 )/2 = 2/3·E·n

Давление газа равно 2/3 от средней кинетической энергии поступательного движения молекул, которые содержатся в единичном объеме газа.

Так как m₀·n = m₀·N/V = m/V = ρ, где ρ – плотность газа, то имеем p = 1/3· ρ· v 2

Объединенный газовый закон.

Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.

Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.

Всякое изменение состояния газа называется термодинамическим процессом.

В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.

Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом.

Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.

Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

где n – концентрация молекул, N – общее число молекул, V – объем газа

Тогда получим 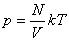или

Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит

При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клайперона.

Уравнение Клайперона можно записать в другой форме.

Здесь N – число молекул в сосуде, ν – количество вещества, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.

Ее численное значение в СИ R = 8,31 Дж/моль·К

называется уравнением состояния идеального газа.

В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`

Для одного моля любого газа это соотношение принимает вид: pV=RT

Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре Е находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.

Запишем уравнение pV=RT для нагретого газа: p ( V + ΔV ) = R (T + 1)

ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:

pS = F – сила давления.

Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.

Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.

Источник