Состоятельность оценок параметров регрессии означает что
Состоятельность оценок параметров регрессии означает что
2.3. Статистические свойства оценок метода наименьших квадратов
Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.
Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.
Предположение относительно независимых переменных
Предположения относительно случайной составляющей модели
При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.
1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так
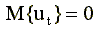 , для всех t =1,2,…,n. , для всех t =1,2,…,n. |
Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения 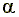
2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так
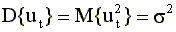 , где дисперсия , где дисперсия 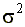 — величина постоянная. — величина постоянная. |
Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).
Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность
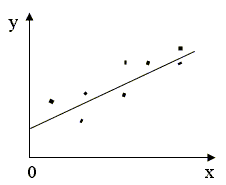
Рис. 2.6а. Гомоскедастичность
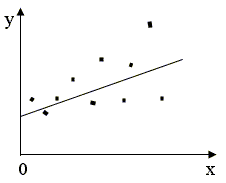
Рис. 2.6б. Гетероскедастичность
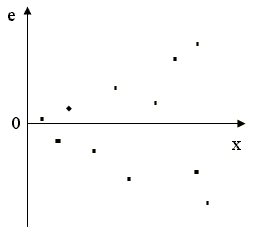
Рис. 2.6в. Гетероскедастичность
3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом
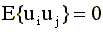 , для всех i не равных j (i, j=1,2,…,n). , для всех i не равных j (i, j=1,2,…,n). |
Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.
4. Четвертое условие Гаусса-Маркова записывается так
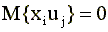 , для всех i и j, , для всех i и j, |
и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.
Дополнительное предположение о нормальном распределении ошибок
Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).
Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.
2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства
Свойства выборочных вариаций (дисперсий) и ковариаций
Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.
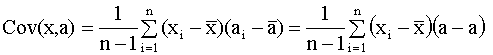 , , |
откуда следует свойство
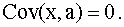
Далее, нетрудно видеть, что имеют место равенства
Состоятельность оценок параметров регрессии означает что
Состоятельность оценок параметров регрессии. Данное свойство состоит в том, что с ростом объема выборки оценка параметра регрессии Ъ сходится к теоретическому значению параметра Р (вычисленного по всей генеральной совокупности), т. е. ошибка оценки стремится к нулю [c.149]
Как было отмечено в 7.1, b — несмещенная и состоятельная оценка параметра р для обобщенной линейной модели множественной регрессии следовательно, и в частном случае, когда мо- [c.156]
Это означает, что при увеличении объема выборки дисперсия оценок параметров регрессии стремится к нулю, то есть оценки параметров регрессии являются состоятельными. [c.107]
Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей б,. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок б, (случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. [c.155]
Как известно (см. гл. 8), при наличии корреляции между ошибками и объясняющими переменными состоятельные оценки параметров в уравнении регрессии можно получить с помощью метода инструментальных переменных. Одна из возможных его реализаций в данном случае выглядит так. Перейдем в уравнении (13.35) к первым разностям [c.381]
Ортогональная регрессия при принятых гипотезах приводит к состоятельным оценкам параметров. [c.33]
Покажите, что в стохастической модели регрессии у = Хр + и с пре положениями (9.18) и (9.19) состоятельная оценка параметра аи есть е е/(п—/г [c.290]
Изучая уравнение линейной регрессии мы предполагали, что реальная взаимосвязь фактора X и отклика 7 линейна, а отклонения от прямой регрессии случайны, независимы между собой, имеют нулевое математическое ожидание и постоянную дисперсию. Если это не так, то статистический анализ параметров регрессии некорректен и оценки этих параметров не обладают свойствами несмещенности и состоятельности. Например, это может быть, если в действительности связь между переменными нелинейна. Поэтому после получения уравнения регрессии необходимо исследовать его ошибки. [c.122]
Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии 6, имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице. [c.156]
Отметим, что при соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии. Применение МНК к моделям авторегрессии ведет к получению смещенных, несостоятельных и неэффективных оценок. [c.280]
Сформулируйте свойства несмещенности, состоятельности и эффективности оценок параметров. Обладают ли этими свойствами оценки. параметров линейной регрессии, полученные с помощью МНК [c.311]
Внутригрупповая регрессия в отличие от статических моделей не позволяет получить состоятельные (при фиксированном Т и при га — > оо) оценки параметров. [c.385]
При анализе временных рядов часто приходится учитывать статистическую зависимость наблюдений в разные моменты времени. Иными словами, для многих временных рядов предположение о некоррелированности ошибок не выполняется. В этом разделе мы рассмотрим наиболее простую модель, в которой ошибки образуют так называемый авторегрессионный процесс первого порядка (точное определение будет дано ниже). Как было показано ранее (глава 5), применение обычного метода наименьших квадратов к этой системе дает несмещенные и состоятельные оценки параметров, однако можно показать (см., например, Johnston and DiNar-do, 1997), что получаемая при этом оценка дисперсии оказывается смещенной вниз, что может отрицательно сказаться при проверке гипотез о значимости коэффициентов. Образно говоря, МНК рисует более оптимистичную картину регрессии, чем есть на самом деле. [c.184]
Состоятельное оценивание дисперсий. Предположим теперь, что в модели (6.1) с гетероскедастичностью для оценки вектора параметра ft используется обычный метод наименьших квадратов. Как установлено в главе 5, эта оценка является состоятельной и несмещенной, однако стандартная оценка ее матрицы ко-вариаций ((3.8), (ЗД9)) V»(/3OLs) — ff2(X X) l смещена и несостоятельна. Отметим, что компьютерные пакеты при оценивании коэффициентов регрессии вычисляют стандартные ошибки коэффициентов регрессии именно по этой формуле. Можно ли сделать поправку на гетероскедастичность и улучшить оценку матрицы ковариаций Положительный ответ дают приводимые ниже два способа оценивания. [c.173]
Обобщенный метод наименьших квадратов. Оценки коэффициентов уравнения регрессии должны отвечать таким критериям, как несмещенность, состоятельность и эффективность.



Оценки коэффициентов уравнения регрессии должны отвечать таким критериям, как несмещенность, состоятельность и эффективность.
Несмещенность оценки коэффициента означает равенство ее математического ожидания «истинному» значению коэффициента (т.е. равенство математического ожидания остатков е нулю):
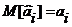
Эффективность оценки коэффициента означает, что оценка коэффициента имеет наименьшую из возможных дисперсию:
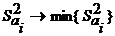
Состоятельность оценки коэффициента означает увеличение ее точности с увеличением числа наблюдений:
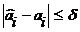

где 
Поскольку обычный МНК позволяет вычислить оценки коэффициентов регрессионного уравнения на основе минимизации суммы квадратов остатков е, для получения несмещенных, состоятельных и эффективных оценок коэффициентов уравнения регрессии, необходимо, чтобы остатки обладали следующими свойствами:
— имели случайный характер;
— имели нулевое математическое ожидание (среднее значение);
— были гомоскедастичными, т.е. имели одинаковую дисперсию 
— были независимыми друг от друга, т.е. неавтокоррелированными;
— были подчинены нормальному закону распределения.
При нарушении свойства гомоскедастичности (т.е. при гетероскедастичности остатков) и при наличии у них автокорреляции, для получения несмещенных, состоятельных и эффективных оценок коэффициентов уравнения используют обобщенный метод наименьших квадратов (ОМНК).
Рассмотрим использование ОМНК при гетероскедастичности остатков. Гетероскедастичность остатков означает, что в различных наблюдениях для независимого фактора 

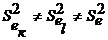


Величина Кt, может меняться при переходе от одного значения фактора хt к другому.
Задача вычисления оценок коэффициентов уравнения регрессии, решаемая в подобной ситуации, состоит в определении величины Кt и внесении поправки в исходные переменные.
При 
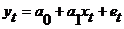
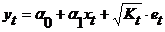
В новом уравнении остатки гетероскедастичны. Предполагая отсутствие их автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные на 

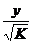

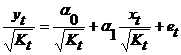
По отношению к обычной регрессии уравнение с новыми, преобразованными переменными, представляет собой взвешенную регрессию, в которой переменные у и х взяты с весами 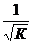
Оценки коэффициентов нового уравнения с преобразованными переменными являются оценками взвешенного (обобщенного) метода наименьших квадратов.
Аналогичный подход к построению уравнения применим и для уравнений множественной регрессии.
Коэффициенты взвешенной модели зависят от предположений относительно коэффициента пропорциональности Кt. В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки 



Следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание, а новое уравнение регрессии имеет иной смысл по сравнению с уравнением регрессии, построенным по исходным данным.
Чтобы убедиться в необходимости использования обобщенного МНК, обычно проводят визуальную проверку гетероскедастичности (строят поле корреляции для значений 
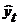
При малом объеме фактических данных для оценки гетероскедастичности используется параметрический тест Гольдфельда-Квандта, который включает в себя следующие шаги.
1. Упорядочение N наблюдений по возрастанию значений переменной x.
3. Разделение совокупности из (N-С) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и построение для каждой из групп уравнений регрессии.
4. Определение суммы квадратов остатков для первой (S1) и второй (S2) групп и нахождение их отношения: R = S1: S2.
При построении регрессионных моделей чрезвычайно важно соблюдение предпосылки МНК об отсутствия автокорреляции остатков, т. е. о распределении значений остатков 
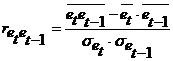
Если этот коэффициент существенно отличен от нуля, то остатки считают автокоррелированными.
10. Выбор вида регрессионной модели и оценка ее параметров
На данном этапе устанавливается однофакторная или многофакторная будет строиться модель и вид модели (линейный или нелинейный).
Обоснование вида модели состоит в выборе вида функции (некоторого аналитического выражения), с помощью которого можно будет описать изменение исследуемого показателя под воздействием факторов.
К обоснованию вида функции идут двумя путями: Теоретическим (анализируя экономическую природу 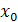

Наиболее употребительными выражениями при описании связи одного фактора и исследуемого показателя являются:
В качестве нелинейных моделей применяются
Для оценки значений параметров регрессионной модели чаще всего используется Метод наименьших квадратов (МНК).Этот метод можно применить как для линейных моделей, так и для нелинейных, допускающих преобразование их к линейному виду путем замены переменных или дифференцированием.
При использовании МНК делаются определенные предпосылки относительно случайной составляющей ε. В модели 

Остатки представляют собой независимые случайные величины, и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.
Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей 
Коэффициенты регрессии, найденные из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, т. к. только в этом случае они могут иметь практическую значимость.
Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Оценки считаются Эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. Состоятельность оценок характеризует увеличение их точности с увеличением объема выработки.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков (
Исследование остатков 
С цель проверки случайного характера остатков 






Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 





Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t и F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки метода наименьших квадратов.
Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок 
Наличие гетероскедастичности в остатках регрессии можно проверить с помощью ранговой корреляции Спирмэна. Суть проверки заключается в том, что в случае гетероскедастичности абсолютные остатки 


Где ρ – абсолютная разность между рангами значений 

Статистическую значимость ρ можно определить с помощью t-критерия:

Принято считать, что если 


При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т. е. распределения остатков 



Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Для того, чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные необходимо преобразовать в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.
Качественные признаки могут приводить к неоднородности исследуемой совокупности, что может быть учтено при моделировании двумя путями:
Качественный фактор может иметь только два состояния, которым будут соответствовать 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.
Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. На основе t-критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.


