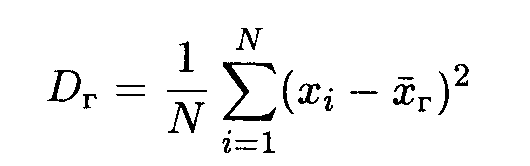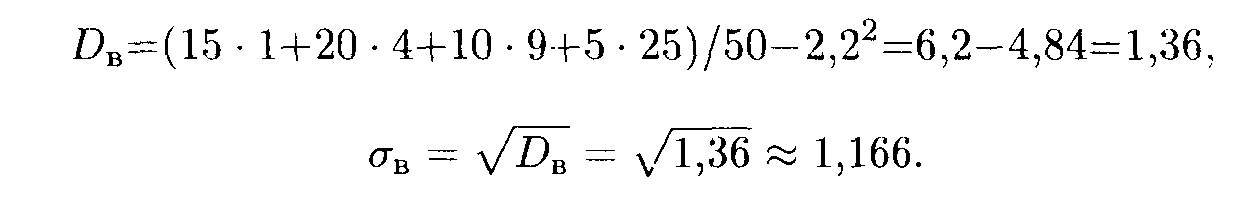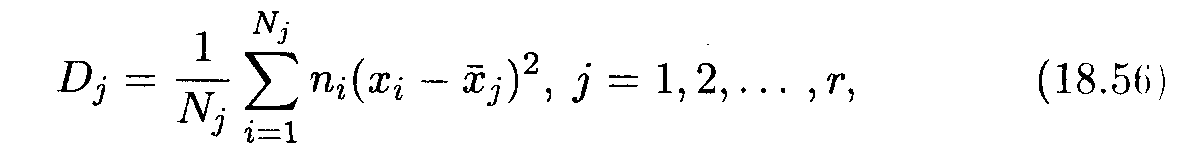Статистические оценки параметров распределения
Статистические оценки параметров распределения
Вы будете перенаправлены на Автор24
Распределения в математической статистике характеризуется многими статистическими параметрами. Оценка неизвестных параметров распределения на основе различных данных выборки позволяет построить распределения случайной величины.
Статистические оценки можно разделить на несмещенные, смещенные, эффективные и состоятельные.
Готовые работы на аналогичную тему
Генеральная и выборочная средние
Величины генерального и выборочного среднего можно найти по следующим формулам:
С этим понятием связано такое понятие как отклонение от средней. Данная величина находится по следующей формуле:
Среднее отклонение обладает следующими свойствами:
Среднее значение отклонения равно нулю.
Генеральная, выборочная и исправленная дисперсии
Еще одними из основных параметров является понятие генеральной и выборочной дисперсии:
Генеральная дисперсия:
Выборочная дисперсия:
С этими понятия связаны также генеральная и выборочная средние квадратические отклонения:
В качестве оценки генеральной дисперсии вводится понятие исправленной дисперсии:
Также вводится понятие исправленного стандартного отклонения:
Пример решения задачи
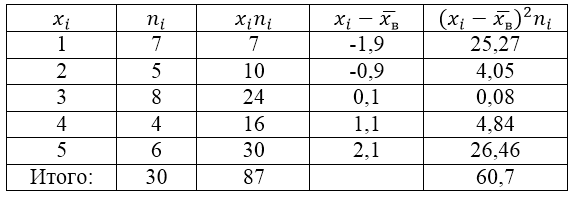
Генеральная совокупность задана следующей таблицей распределения:
Найдем для нее генеральное среднее, генеральную дисперсию, генеральное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.
Для решения этой задачи для начала сделаем расчетную таблицу:
Найдем генеральную дисперсию по формуле:
Генеральное среднее квадратическое отклонение:
Исправленное среднее квадратическое отклонение:
Статистические оценки параметров распределения
Несмещенной называется статистическая оценка 

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки п. Состоятельной называется статистическая оценка типа (18.50), которая при п > 
Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
и выборочная средняя
Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.
Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это генеральная дисперсия:
и выборочная дисперсия:
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид
Генеральное среднее квадратическое отклонение определяется как
Аналогично вводится и выборочное среднее квадратическое отклонение
Пример 4. Выборка задана таблицей распределения
Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. По формуле (18.52) сначала находим 
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:
Виды дисперсий
Часто значения количественного признака Х совокупности разбиваются на определенное число групп. Каждую группу можно рассматривать как самостоятельную выборку, и для каждой группы можно определить групповую среднюю и дисперсию. Пусть r — число групп. Групповой дисперсией на зывается дисперсия значений признака в группе относительно групповой средней:
где ni — частота значения xi в группе, j — номер группы 

Зная дисперсию каждой группы, можно определить их среднюю арифметическую. Внутригрупповой дисперсией называется средняя арифметическая дисперсий, где каждое слагаемое входит с весом объема группы:
В свою очередь, зная для всех групп средние 

где п = 
Для общей дисперсии всей совокупности справедлива следующая теорема, которая приводится здесь без доказательства.
ТЕОРЕМА 6. Если совокупность состоит из нескольких групп, то общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий:
где слагаемые в правой части определяются соответственно формулами (18.57) и (18.58).
Поясним сказанное в этом пункте на примере.
Пример 5. Совокупность состоит из двух следующих групп:
Найти групповые, внутригрупповую, межгрупповую и общую дисперсии.
Решение. Объемы групп соответственно равны N1 = 10 и N2 = 5. Общий объем совокупности: п = 10 + 5 = 15. Найдем групповые средние:
Теперь находим групповые дисперсии по формуле (18.56):
Внутригрупповая дисперсия, согласно формуле (18.57), равна:
Теперь найдем межгрупповую дисперсию по формуле (18.58), для чего сначала определим общую среднюю:
Наконец, общая дисперсия, согласно формуле (18.59), равна:
Статистические оценки параметров генеральной совокупности
Определение статистической оценки. Точечные статистические оценки: смещенные и несмещенные, эффективные и состоятельные. Интервальные статистические оценки. Точность и надежность оценки; определение доверительного интервала; построение доверительных интервалов для средней при известном и неизвестном среднеквадратическом отклонении.
Определение статистической оценки
Точечные статистические оценки
Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Поэтому нужно потребовать, чтобы математическое ожидание оценки было равно оцениваемому параметру. Соблюдение требования устраняет систематические ошибки.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки ) имеет наименьшую возможную дисперсию. При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при стремится к нулю, то такая оценка оказывается также состоятельной.
Рассмотрим вопрос о том, какие выборочные характеристики лучше всего в смысле несмещённости, эффективности и состоятельности оценивают генеральную среднюю и дисперсию.
Пусть изучается дискретная генеральная совокупность относительно количественного признака. Генеральной средней называется среднее арифметическое значений признака генеральной совокупности. Она вычисляется по формуле
где — значения признака генеральной совокупности объема ; — соответствующие частоты, причем
где — значения, признака в выборочной совокупности объема ; — соответствующие частоты, причем
Если дисперсии двух совокупностей одинаковы, то близость выборочных средних к генеральным не зависит от отношения объема выборки к объему генеральной совокупности. Она зависит- от объема выборки: чем больше объем выборки, тем меньше выборочная средняя отличается от генеральной.
Интервальные оценки
Наряду с точечным оцениванием, статистическая теория оценивания параметров занимается вопросами интервального оценивания. Задачу интервального оценивания можно сформулировать так: по данным выборки построить числовой интервал, относительно которого с заранее выбранной вероятностью можно сказать, что внутри него находится оцениваемый параметр. Интервальное оценивание особенно необходимо при малом количестве наблюдений, когда точечная оценка малонадежна.
Доверительный интервал для генеральной средней при известном значении среднего квадратического отклонения и при условии, что случайная величина (количественный признак ) распределена нормально, задается выражением
где — наперед заданное число, близкое к единице, а значения функции приведены в таблице прил. 2.
Доверительный интервал для генеральной средней нормального распределения признака при неизвестном значении среднего квадратического отклонения задается выражением
18.6.5. Статистические оценки параметров распределения
Несмещенной называется статистическая оценка 

Смещенной называется оценка, при которой условие (18.51) не выполнено. Эффективной называется оценка, которая имеет минимальную дисперсию при заданном объеме выборки П. Состоятельной называется статистическая оценка типа (18.50), которая при П > 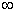
Теперь укажем виды числовых характеристик оценок. Прежде всего, это средние. Генеральная средняя для изучаемого количественного признака Х по генеральной совокупности
И Выборочная средняя
Можно показать, что выборочная средняя (18.52) является несмещенной оценкой; это аналог математического ожидания случайной величины.
Введем в рассмотрение величины, характеризующие отклонение значений количественного признака Х от своего среднего значения. Это Генеральная дисперсия:
И выборочная дисперсия:
Можно показать, что для вычисления этих характеристик справедливы более удобные формулы, аналогичные дисперсии случайной величины; так, формула (18.53) принимает вид
Генеральное среднее квадратическое отклонение определяется как
Аналогично вводится и Выборочное среднее квадратическое отклонение
Пример 4. Выборка задана таблицей распределения
Найти выборочные характеристики: среднюю, дисперсию и среднее квадратическое отклонение.
Решение. По формуле (18.52) сначала находим 
Затем по формулам (18.54) и (18.55) находим две другие искомые величины:
Тема 3.3. Статистические оценки параметров распределения
Свойства статистических оценок
Методы нахождения точечных оценок
Интервальное оценивание параметров
Доверительный интервал для математического ожидании при известной дисперсии нормально распределённой генеральной совокупности.
Распределение хи-квадрат и распределение Стьюдента.
Доверительный интервал для математического ожидании случайные величины, имеющей нормальное распределение при неизвестной дисперсии.
Доверительный интервал для среднего квадратического отклонения нормального распределения.
Вентцель, Е.С. Теория вероятностей [Текст] / Е.С. Вентцель. – М.: Высшая школа, 2006. – 575 с.
П.1. Понятие оценки
Такие распределения, как биномиальное, показательное, нормальное, являются семействами распределений, зависящими от одного или нескольких параметров. Например, показательное распределение с плотностью вероятностей 
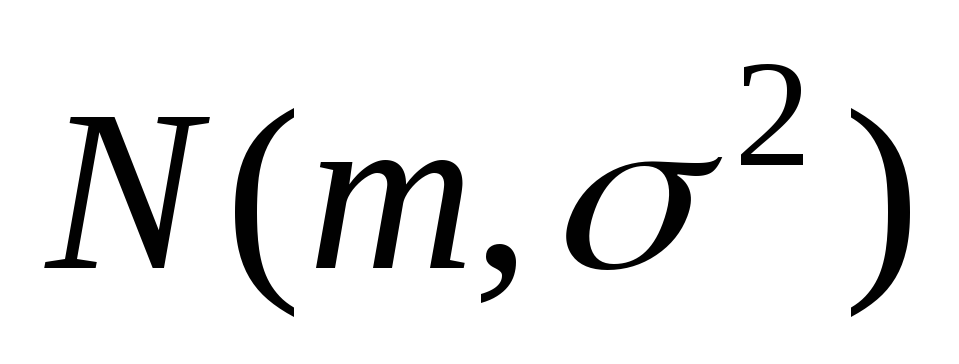
Пусть закон распределения генеральной совокупности определён с точностью до значений входящих в его распределение параметров 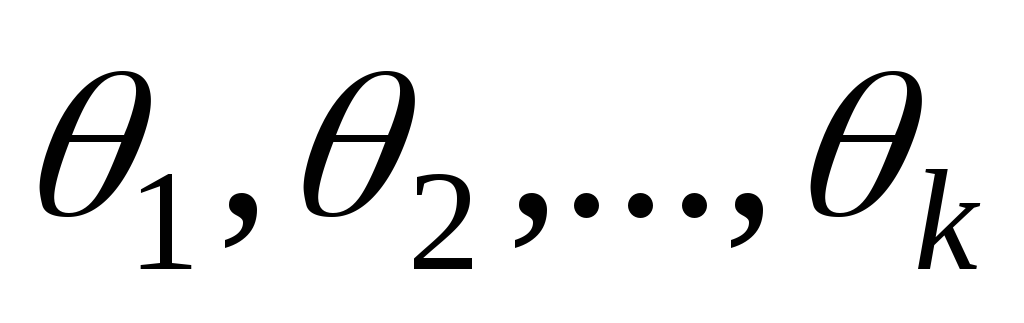



Статистической оценкой (в дальнейшем просто оценкой) 
Оценка 

Существует два вида оценок – точечные и интервальные.
Точечной называется оценка, определяемая одним числом. При малом числе наблюдений эти оценки могут приводить к грубым ошибкам. Чтобы избежать их, используют интервальные оценки.
Интервальной называется оценка, которая определяется двумя числами – концами интервала, в котором с заданной вероятностью заключена оцениваемая величина θ.
П. 2 Свойства статистических оценок
Величину 
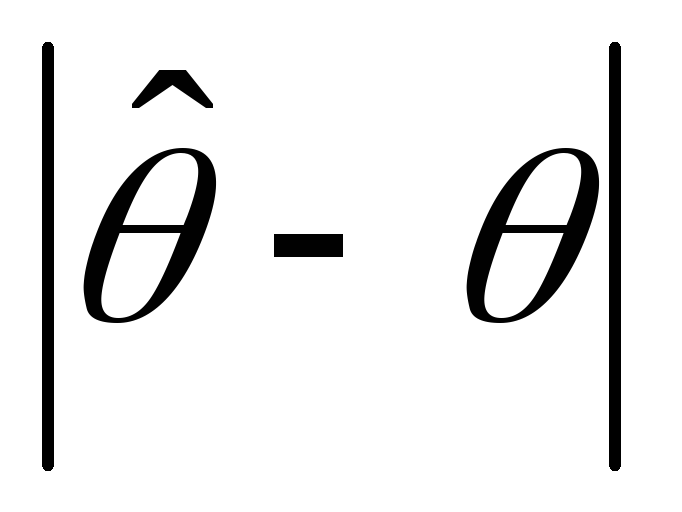
К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т.е. быть в каком-то смысле «доброкачественной» оценкой. Качество оценки определяют, проверяя, обладает ли она свойствами несмещённости, эффективности и состоятельности.
Оценка 

Если равенство (1) не имеет места, то оценка 
Для некоторых задач математической статистики может существовать несколько несмещённых оценок. Обычно предпочтение отдают той, которая обладает наименьшим рассеянием (дисперсией).
Оценка 
Пусть D(

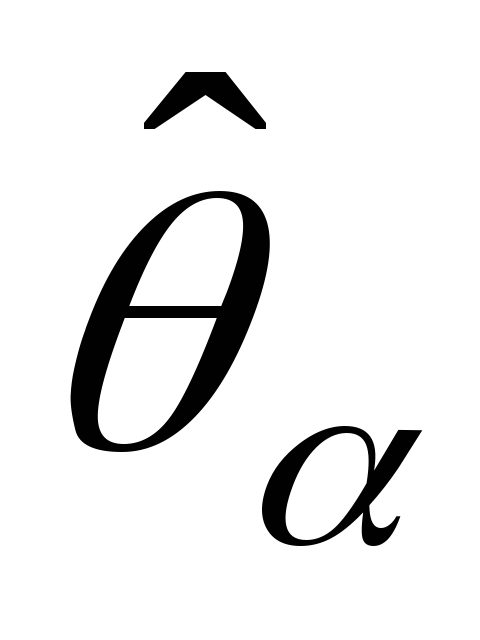


Ясно, что 




Замечание: Если оценка 


Оценка 


Состоятельность оценки 

Теорема 1. Выборочная средняя является несмещённой и состоятельной оценкой математического ожидания.
Теорема 2. Исправленная выборочная дисперсия является несмещённой и состоятельной оценкой дисперсии.
Теорема 3. Эмпирическая функция распределения выборки является несмещённой и состоятельной оценкой функции распределения случайной величины.