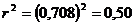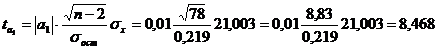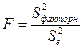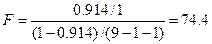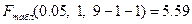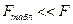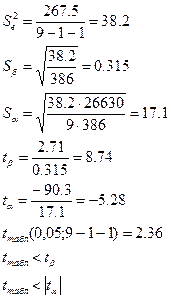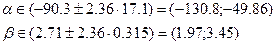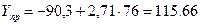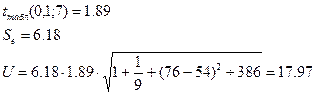Статистическая значимость параметров уравнения регрессии

Оценка статистической значимости параметров уравнения регрессии.

С помощью МНК можно получить лишь оценки параметров уравнения регрессии. Чтобы проверить, значимы ли параметры (т.е. значимо ли они отличаются от нуля в истинном уравнении регрессии) используют статистические ме­тоды проверки гипотез. В качестве основной гипотезы вы­двигают гипотезу о незначимом отличии от нуля параметра регрессии или коэффициента корреляции. Альтернативной гипотезой, при этом является гипотеза обратная, т.е. о неравенстве нулю параметра или коэффициента корреляции. Для проверки гипотезы используется t-критерий Стьюдента.

Найденное по данным наблюдений значение t-критерия (его еще называют наблюдаемым или фактиче­ским) сравнивается с табличным (критическим) значением, определяемым по таблицам распределения Стьюдента (ко­торые обычно приводятся в конце учебников и практикумов по статистике или эконометрике). Табличное значение оп­ределяется в зависимости от уровня значимости и числа степеней свободы, которое в случае линейной парной рег­рессии равно , n-число наблюдений.

Если фактическое значение t-критерия больше таб­личного (по модулю), то считают, что с вероятностью параметр регрессии (ко­эффициент корреляции) значимо отличается от нуля.

Если фактическое значение t-критерия меньше таб­личного (по модулю), то нет оснований отвергать основную гипотезу, т.е. параметр регрессии (коэффициент корреля­ции) незначимо отличается от нуля при уровне значимости .

Фактические значения t-критерия определяются по формулам:

,

,

где .

Для проверки гипотезы о незначимом отличии от нуля коэффициента линейной парной корреляции используют критерий:

,

где r — оценка коэффициента корреляции, полученная по наблюдаемым данным.

Прогноз ожидаемого значения результативного признака Y по линейному парному уравнению регрессии.

Пусть требуется оценить прогнозное значение призна­ка-результата для заданного значения признака-фактора 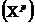. Прогнозируемое значение признака-результата с дове­рительной вероятностью равной принадлежит интервалу прогноза:

,

где — точечный прогноз;

t — коэффициент доверия, определяемый по таблицам распределения Стьюдента в зависимости от уровня значимости α и числа степеней свободы ;

— средняя ошибка прогноза.

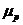
Точечный прогноз рассчитывается по линейному уравнению регрессии, как:

.

Средняя ошибка прогноза определяется по формуле:

.

Пример 1.

На основе данных, приведенных в Приложении и соответствующих варианту 100, требуется:

2. Рассчитать линейный коэффициент парной корреляции и коэффициент детерминации. Сделать выводы.

3. Оценить статистическую значимость параметров регрессии и коэффициента корреляции с уровнем значимости 0,05.

4. Выполнить прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X, составляющим 105% от среднего уровня X. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал с вероятностью 0,95.

Решение:

В качестве признака-фактора в данном случае выберем курсовую цену акций, так как от прибыльности акций зависит величина начисленных дивидендов. Таким образом, результативным будет признак дивиденды, начисленные по результатам деятельности.

Для облегчения расчетов построим расчетную таблицу, которая заполняется по ходу решения задачи. (Таблица 1)

Для наглядности зависимости Yот X представим графически. (Рисунок 2)

1. Построим уравнение регрессии вида: .

Для этого необходимо определить параметры уравнения и .

Определим ,

где — среднее из значений , возведенных в квадрат;

— среднее значение в квадрате.

Получим уравнение регрессии следующего вида:

Параметр показывает, сколько составили бы дивиденды, начисленные по результатам деятельности при отсутствии влияния со стороны курсовой цены акций. На основе параметра можно сделать вывод, что при изменении курсовой цены акций на 1 руб. произойдет изменение дивидендов в ту же сторону на 0,01 млн. руб.

2. Рассчитаем линейный коэффициент парной корреляции и коэффициент детерминации.

Линейный коэффициент парной корреляции определим по формуле:

,

Определим и :

Коэффициент корреляции, равный 0,708, позволяет судить о тесной связи между результативным и факторным признаками .

Коэффициент детерминации равен квадрату линейного коэффициента корреляции:

Коэффициент детерминации показывает, что на вариации начисленных дивидендов зависит от вариации курсовой цены акций, и на — от остальных неучтенных в модели факторов.

3. Оценим значимость параметров уравнения регрессии и линейного коэффициента корреляции по t-критерию Стьюдента. Необходимо сравнить расчетные значения t-критерия для каждого параметра и сравнить его с табличным.

Для расчета фактических значений t-критерия определим :

Далее определим _. при уровне значимости и числе степеней свободы равном :

Сравним и с : , следовательно, оба параметра уравнения регрессии признаются значимыми.

Проверим значимость линейного коэффициента корреляции:

Сравниваем с уже известным нам значением , следовательно, линейный коэффициент корреляции существенен.

4. Выполним прогноз ожидаемого значения признака-результата Yпри прогнозном значении признака-фактора X,составляющим от среднего уровня X.

Точечный прогноз рассчитывается по линейному уравнению регрессии:

,

В нашем случае

Тогда

Оценим ошибку прогноза:

После этого определим интервал, к которому с вероятностью 0,95 принадлежит прогнозное значение признака Y:

,

где 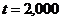– табличное значение t-критерия при и числе степеней свободы

.

В данном случае интервал будет такой:

То есть, с вероятностью 0,95 прогнозируемая величина дивидендов при курсовой стоимости акций равной 101,43 руб. будет принадлежать интервалу от 19,8 до 20,7 млн. руб.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

Проверка статистической значимости уравнения регрессии и его параметров

а) проверка статистической значимости уравнения:

Проверка значимости (существенности) уравнения регрессии позволяет установить, существенна ли связь включенных в уравнение признаков (Y и X), соответствует ли математическая модель, выражающая зависимость Y и X, фактическим данным и достаточно ли включенных в уравнение объясняющих переменных Х для описания зависимой переменной Y. Иными словами оценка значимости уравнения регрессии позволяет узнать пригодно ли оно для практического использования (например, для прогнозирования) или нет.

Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера:

или в терминах коэффициента детерминации

,

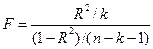
где n – длина совокупностей данных, k – количество факторов, включенных в модель (в уравнении парной регрессии k=1).

Уравнение регрессии статистически значимо, если

.

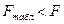
1) определяется максимальной величиной отношения дисперсий , которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы (нулевая гипотеза о незначимости уравнения в целом);

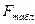
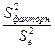
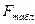
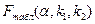
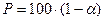
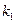
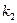
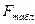
2) для определения можно использовать статистическую функцию FРАСПОБР, предварительно задав три параметра , где – заданный уровень значимости проверки или уровень вероятности ( связано с вероятностью Р формулой ); – число степеней свободы числителя, равное количеству k факторов, включенных в модель; – число степеней свободы знаменателя (n-k-1). Таким образом, зависит от заданной вероятности, числа уровней в совокупностях данных и вида уравнения регрессии.

Пример (продолжение).

4) Проверить значимость уравнения регрессии с помощью F-критерия Фишера ( =0,05)

вывод: уравнение регрессии статистически значимо, связь включенных в него признаков существенна;

Значение F-критерия можно получить также в таблице «Дисперсионный анализ» отчета по работе с инструментом регрессия (рис. 13).

Рис. 13. Фрагмент регрессионного анализа

а) проверка статистической значимости параметров уравнения:

В линейной регрессии обычно оценивается значимость не только уравнения регрессии, но и отдельных его параметров. Для этого применяется t-критерий Стьюдента:

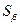
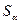
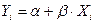
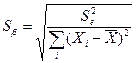
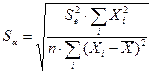
1) рассчитывают стандартные ошибки (среднеквадратические отклонения) и каждого из параметров уравнения по формулам

, ,

где 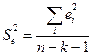–остаточная дисперсия, k – число факторов в уравнении регрессии (в нашем случае k=1);

2) определяют расчетные значения t-критерия Стьюдента:

, ;

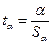
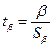
3) определяют табличное значение t-критерия 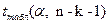с помощью статистической функции СТЬЮДРАСПОБР по двум параметрам: заданному уровню значимости и одной степени свободы (n-k-1);

4) параметры уравнения регрессии будут статистически значимы, если выполняются неравенства:

, .

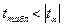
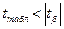
Замечания:

1) статистическая значимость (незначимость) коэффициента регрессии 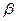означает одновременно статистическую значимость (незначимость) фактора Х, включенного в уравнение; статистически незначимый (или несущественный) фактор должен быть устранен из модели или заменен другим;

2) статистическая значимость (незначимость) параметра уравнения означает верную (неверную) спецификацию модели; под спецификацией понимают:

а) выбор вида уравнения;

б) определение независимых факторов для включения в модель;

3) t-критерий можно использовать также для определения интервальных оценок параметров модели:

,

.

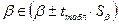
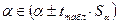
Поскольку коэффициент регрессии 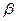в эконометрических исследованиях имеет четкую экономическую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, то есть не должны содержать одновременно положительные и отрицательные величины и даже нуль.

Пример (продолжение).

4) осуществить проверку значимости параметров уравнения регрессии по t-критерию Стьюдента ( =0,05)

Вывод: оба параметра модели статистически значимы.

Дополнение: интервальные оценки параметров

Расчетные значения t-критерия, а также интервальные оценки параметров можно найти в отчете по результатам работы с инструментом Регрессия (рис. 14).

Рис. 14. Фрагмент регрессионного анализа

2.4. Экономический прогноз

Рассматриваемая модель 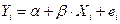может быть использована для определения прогнозных оценок исследуемой величины. При прогнозировании на основе регрессионных моделей можно выделить три основных этапа:

1) точечный прогноз фактора Х;

2) точечный прогноз показателя Y;

3) интервальный прогноз показателя Y.

Рассмотрим содержание этих этапов подробнее.

1) точечный прогноз фактора Хв зависимости от специфики исходных данных и условия задачи можно определить одним из следующих способов:

а) если исходные данные являются временными рядами, то для прогноза фактора можно воспользоваться методами экстраполяции и использовать наиболее подходящую модель временного ряда

.

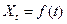
Тогда прогноз фактора на k шагов вперед определяется по формуле

.

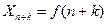
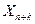
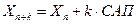
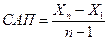
б)вслучае временных рядов можно найти также с помощью среднего абсолютного прироста (САП) по формуле

, .

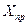
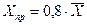
в)если исходные данные являются пространственными, то, очевидно, в задаче будет задано правило для определения . Например, если прогнозное значение фактора составляет 80 % от его среднего значения, то .

2) точечный прогноз показателя Yнаходят подстановкой в модель прогнозных значений фактора:

– в случае пространственных данных,

– в случае временных рядов.

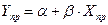
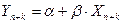
3) интервальный прогноз показателя Y:

вначале находят ошибку прогнозирования

,

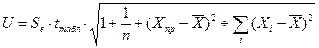
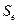
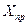
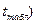
которая зависит от стандартной ошибки модели , удаления от своего среднего значения, количества наблюдений n, заданного уровня вероятности попадания в интервал прогноза (он определяет величину ;

затем находят сам доверительный интервал прогноза:

нижняя граница интервала – ,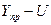

верхняя граница интервала – .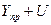

Пример (продолжение).

5) осуществить прогнозирование среднего значения показателя Y при уровне значимости =0,1, если прогнозное значение фактора Х составит 117 % от его максимального значения

1) точечный прогноз фактора Х

,

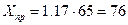
2) точечный прогноз показателя Y

3) интервальный прогноз показателя Y

Нижняя граница интервала: 115,66-17,97=97,69

Верхняя граница интервала: 115,66+17,97=133,63.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник