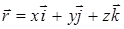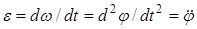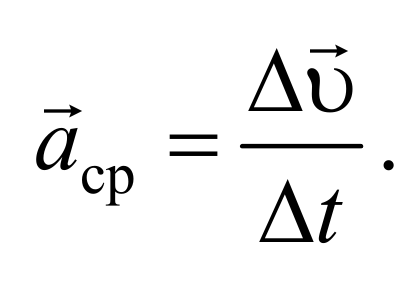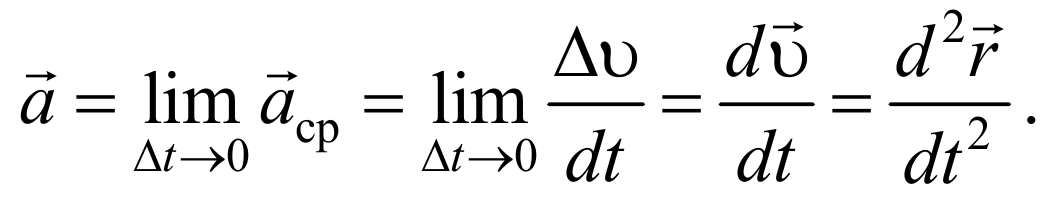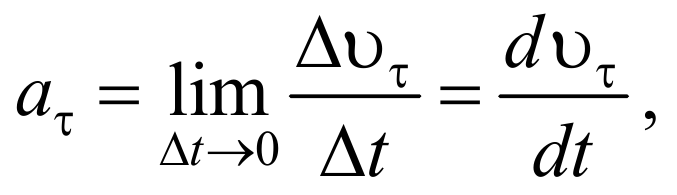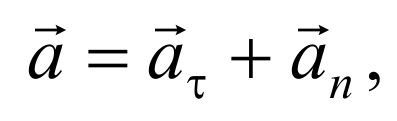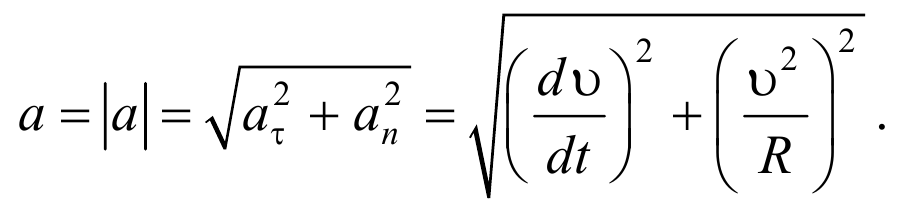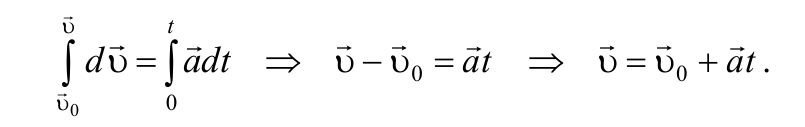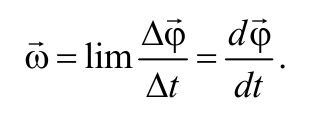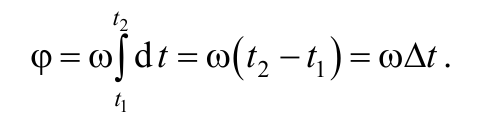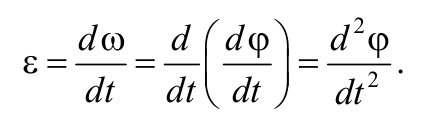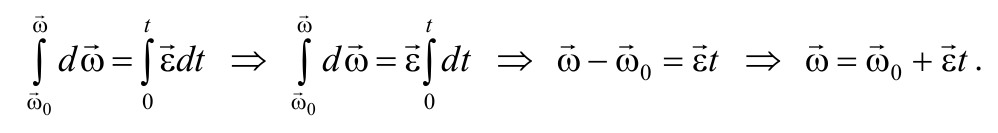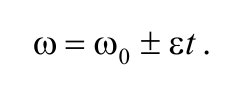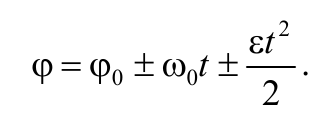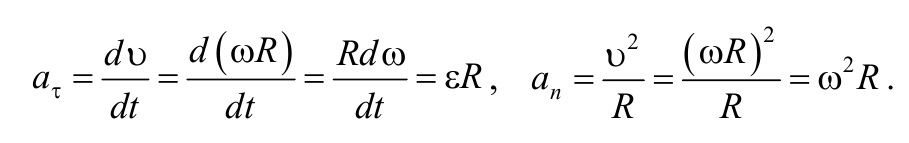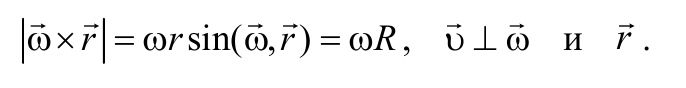Связь линейных и угловых кинематических параметров

Угловые кинематические величины. Связь линейных и угловых кинематических величин.

Угловой скоростьюназывается векторная величина, равная первой производной угла поворота тела по времени: ⁡.Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dф. Размерность угловой скорости dim = , а ее единица — радиан в секунду (рад/с). Линейная скорость точки ,т.е. . Если = const, то вращение равномерное и его можно характеризовать периодом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2 . Так как промежутку времени соответствует , то откуда Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называет- называется частотой вращения: ,откуда . Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: .Связь линейных и угловых кинематических величин:связь между линейными (длина пути s, пройденного точкой дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нор-нормальное ускорение ) и угловыми величинами (угол поворота , угловая скорость , угловое ускорение выражается следующими формулами: , и , , , и .

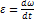
7.Задачи динамики. Инерциальные системы отсчета. Первый закон Ньютона. Преобразования Галилея. Принцип относительности.

8.Сила. Масса. Законы Ньютона. Типы сил в механике.

. 9.Силы трения. Трение покоя и трение скольжения. Зависимость сил трения от скорости.

Источник

Вопрос 5. Связь между линейными и угловыми кинематическими характеристиками

Вопрос1 Классическая механика и границы ее применимости. Материальная точка. Система отсчета. Кинематические уравнения

Классическую механику подразделяют на кинематику, статику и динамику.

Материальная точка- тело, размерами которого можно пренебречь. Движение материальной точки по отношению к системе отсчета может быть задано векторным или координатным способами.

При векторном способе положение точки А, рис. 1, в момент времени t определяется ее радиусом вектором , проведенным из начала координат до движущейся точки.

Закон движения дается векторным уравнением . При координатном способе положение точки А определяется координатами x, y, z, а закон движения задается тремя уравнениями:

при этом

Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом.

Вопрос 2 Траектория, путь, перемещение. Средняя и мгновенная скорости. Равномерное прямолинейное движение

Непрерывная линия, которую описывает точка при своем движении, называется траекторией. Путь – это длина траектории, пройденная точкой.

Перемещение- изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения

Мгновенная скорость

Средняя скорость Vср=S/t

Вопрос 3 Ускорение. Нормальная и тангенциальная составляющие ускорения. Равнопеременное движение

Ускорение- быстрота изменения скорости

Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости

Нормальное ускорение возникает всегда при движении точки по траектории с ненулевой кривизной. Характеризует изменение скорости по направлению.

=

Равнопеременное движение — движение с постоянным ускорением.

x(t)=x0+V0t+at /2

Вопрос 4 Движение материальной точки по окружности. Угол поворота, угловая скорость, угловое ускорение

Рассмотрим движение материальной точки по окружности радиуса R Пусть за время точка повернется на угол , тогда угловая скорость

,

Угловое ускорение характеризует быстроту изменения угловой скорости, т.е.

Вопрос 5. Связь между линейными и угловыми кинематическими характеристиками

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.

При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путь

Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

При движении точки по кривой линейная скорость направлена по касательной к кривой и по модулю равна произведению угловой скорости на радиус кривизны кривой.

Источник

§5. Угловые кинематические параметры и их связь с линейных кинематическими параметрами.

При вращении тела все точки тела движутся по окружностям, центры которых лежат на оси вращения. Эта ось может быть либо неподвижной, либо как-то перемещаться в пространстве. Однако мгновенное распределение скоростей точек тела в рассматриваемый момент времени будет в точности таким же, как и при вращении тела вокруг неподвижной оси. Движение тела в этом случае называют мгновенным вращением. Прямая, проходящая через точки тела, скорость которых равна нулю, называется мгновенной осью вращения. В общем случае мгновенная ось вращения может проходить и вне тела.

Мгновенная ось служит для описания мгновенного распределения толькоскоростей. Той же осью нельзя пользоваться для описания мгновенного распределения ускорений.

Опишем движение материальной точки по окружности радиуса R и для этого введем следующие угловые кинематические параметры. (рис. 5.1.).

1. Элементарное угловое перемещение d.

Элементарное угловое перемещение точки характеризуется не только абсолютной величиной, но и плоскостью, в которой происходит это перемещение. Значит это не скалярная величина. Направление этой величины примем условно, и поэтому получится так называемый псевдовектор. Псевдовектор отличается от вектора тем, что при инверсии координатных осей компоненты вектора меняют свой знак, а компоненты псевдовектора нет.

Направление элементарного угла поворота d определяется по правилу правого винта: оно совпадает с направлением поступательного движения правого винта, вращающегося вместе с точкой (рис. 5.1.). Бесконечно малые (элементарные) углы поворота d удовлетворяют правилу сложения векторов.

Конечные углы поворотов  этому правилу не удовлетворяют, и поэтому не могут считаться векторами.

Из рис. 5.1 также следует, что

Действительно, dr= Rd = r sin d,а направления всех векторов удовлетворяют правилу векторного умножения.

Равенство 5.1 выражает связь между линейным кинематическим параметром (элементарным перемещением dr) и угловым кинематическим параметром (элементарным углом поворота d).

2. Угловая скорость

Для описания вращательного движения точки вводят понятие вектора угловой скорости , численно равного производной от угла поворота  по времени t. Направление вектора  совпадает с направлением элементарного углового перемещения d, т.е. определяется по правилу правого винта, введенному выше.

.(5.2)

Связь между скоростью v точки при вращательном движении и угловой скоростью можно найти из определения скорости (3.4) и соотношения (5.1).

= r. (5.3)

3. Угловое ускорение

Угловым ускорением называется производная вектора угловой скорости по времени.

 = .(5.4)

Найдем связь между линейным ускорением и угловыми кинематическими параметрами. Для этого воспользуемся определением ускорения (3.9) и соотношением (5.3):

w=.(5.5)

Соотношение (5.5) выражает связь между линейным ускорением w и угловыми кинематическими параметрами и  в общем случае.

В случае вращения точек тела вокруг неподвижной оси вектора  и r лежат в одной плоскости, а  и v взаимно перпендикулярны (см. рис. 5.2).

Очевидно, что модуль полного ускорения w равен:

. (5.7)

Уравнения (5.1)(5.7) выражают связь между угловыми и линейными кинематическими параметрами.

Источник

Лекция №2. Элементы кинематики

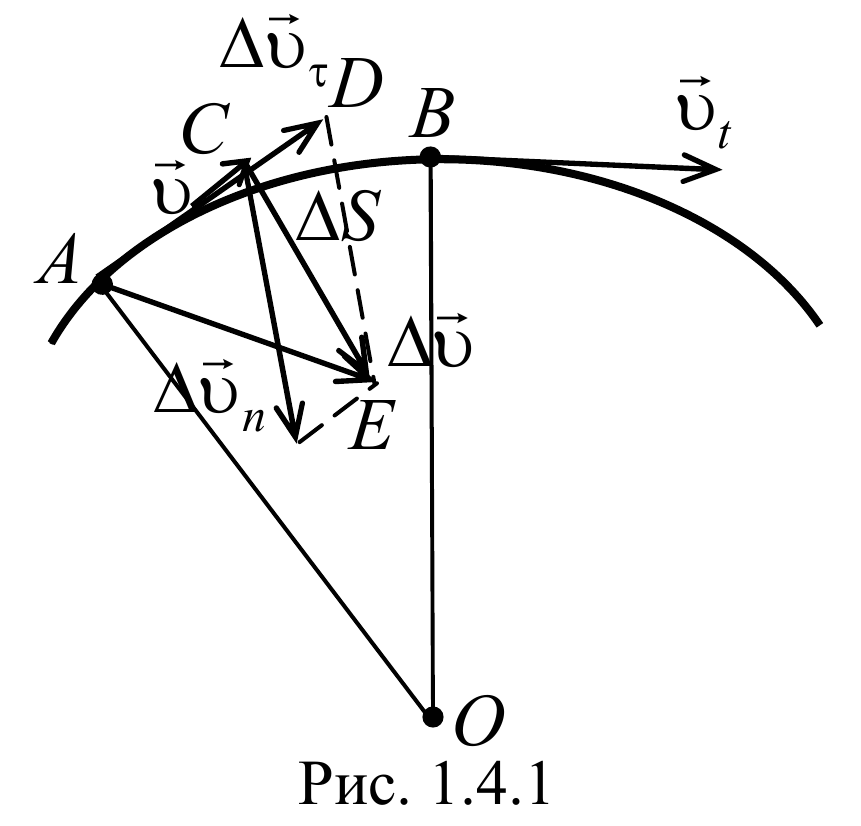
1.4. Нормальное и тангенциальное ускорения при криволинейном движении

В общем случае при движении тела его скорость изменяется как по величине, так и по направлению. Для характеристики быстроты изменения скорости движения вводится понятие ускорения.

Таким образом, ускорение есть векторная величина, равная первой производной скорости по времени.

Тангенциальная составляющая ускорения

т.е. равна первой производной по времени от модуля скорости, определяя тем самым быстроту изменения скорости по модулю.

называется нормальной составляющей ускорения и направлена по нормали к траектории к центру ее кривизны. Поэтому эту составляющую ускорения называют также центростремительным ускорением.

Таким образом, полное ускорение тела a есть геометрическая сумма тангенциальной a_τ и нормальной a_n составляющих

Тангенциальное ускорение равно первой производной по времени от модуля скорости и определяет быстроту изменения скорости по модулю, и направлено по касательной к траектории.

Нормальное ускорение определяет быстроту изменения скорости по направлению и направлено к центру кривизны траектории.

Векторы a_τ и a_n взаимно перпендикулярны поэтому модуль полного ускорения равен

1.5. Классификация движений материальной точки

В зависимости от тангенциальной и нормальной составляющих ускорения движение можно классифицировать следующим образом:

3) a_τ= ƒ(t), a_n=0 − прямолинейное движение с переменным ускорением.

5) a_τ=const, a_n≠const − равнопеременное движение по окружности.

6) a_τ=0, a_n≠0 − равномерное криволинейное движение.

7) a_τ=const, a_n≠0 − криволинейное равнопеременное движение.

1.6. Кинематика абсолютно твердого тела

Угловой скоростью тела называется вектор, численно равный первой производной по времени от угла поворота тела по времени и направленный вдоль оси вращения по правилу правого винта:

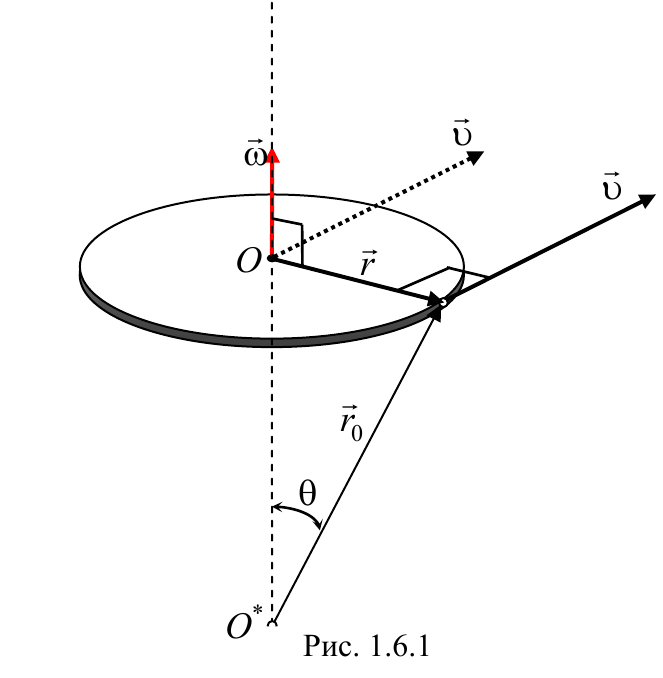
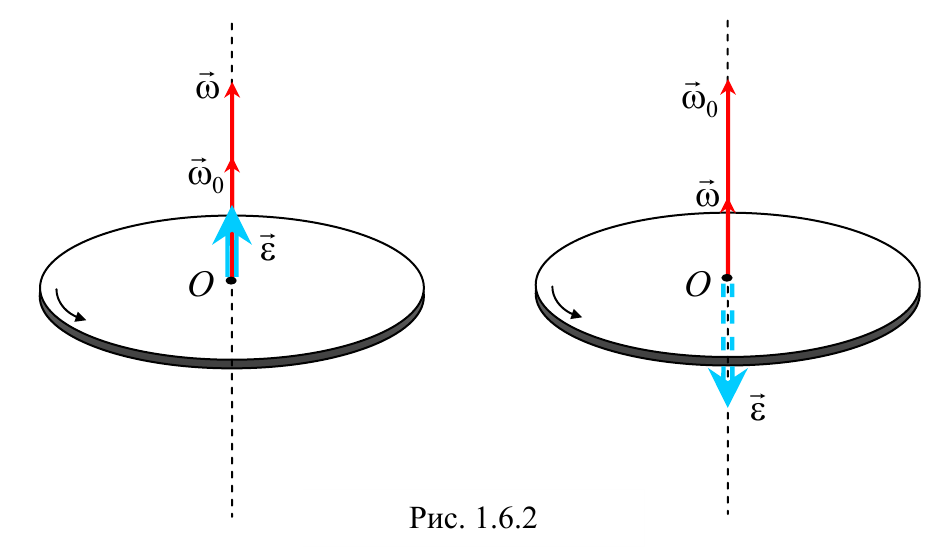
Вектор угловой скорости направлен по оси вращения, причем так, чтобы вращение, рассматриваемое с конца вектора угловой скорости, происходило против хода часовой стрелки (рис 1.6.1). Единицей угловой скорости является рад/с.

Скорость произвольной точки вращающегося тела называется линейной скоростью этой точки.

Равномерное вращение характеризуется периодом вращения и частотой вращения.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

При ускоренном вращении вектор углового ускорения сонаправлен с вектором угловой скорости, а при замедленном − противоположен ему.

В случае равнопеременного движения точки по окружности (ε = const) угловая скорость определяется по формуле

Или в скалярном виде

Проинтегрировав выражение (1.6.1) можно получить формулу для угла поворота тела

1.7. Связь между линейными и угловыми характеристиками тела при его вращении

Тангенциальная и нормальная составляющие ускорения произвольной точки тела, вращающегося вокруг неподвижной оси, определяются формулами:

Источник

Связь линейных и угловых кинематических характеристик

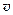
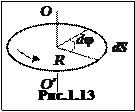
¨Связь линейной и угловой скоростей

.

Пусть некоторая точка вращающегося тела движется по окружности (рис 1.13) радиуса . За время она сместится на угол , пройдя путь . Т.к. , то, разделив на обе части , получим представленное выше соотношение. В отличие от угловой скорости, которая одинакова для всех точек тела, линейная возрастает с увеличением расстояния от оси вращения.

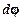
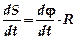
¨ Связь тангенциального и углового ускорений

Т.к. тангенциальное ускорение и , то .

¨ Связь нормального ускорения и угловой скорости

Т.к. нормальное ускорение и , то

¨Таблица соответствия кинематических характеристик

Поступательное движение	Вращательное движение

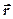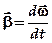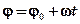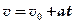Глава 2

ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ

Динамикаизучает влияние взаимодействия тел на механическое движение.

В основе динамики поступательного движения тела лежат три закона Ньютона.

Первый закон Ньютона

¨Первый закон Ньютона: тело покоится или движется равномерно и прямолинейно до тех пор, пока на него не подействуют другие тела.

Стремление тела сохранять свою скорость называется инертностью, а движение тела, свободного от воздействия других тел, — движением по инерции.

Первый закон Ньютона выполняется только в инерциальных системах отсчета — системах, вектор скорости которых не меняется с течением времени.

¨Инерциальная система отсчета— это система, в которой выполняется первый закон Ньютона, т.е. свободная материальная точка либо покоится, либо движется равномерно и прямолинейно.

Любая система отсчета, движущаяся равномерно и прямолинейно относительно некоторой инерциальной системы, также является инерциальной. Можно заключить, что инерциальных систем множество. Все инерциальные системы эквивалентны. Однако в одних инерциальных системах тело может покоиться, в других двигаться. Следовательно, механическое движение относительно.

Системы отсчета, движущиеся с ускорением, называются неинерциальными, например, тормозящий автобус.

В дальнейшем мы будем использовать только инерциальные системы отсчета.

¨Инертность — способность тела сохранять свою скорость.

Действительно, чем труднее изменить скорость тела, тем более инертным оно считается. Вместе с тем, труднее всего изменить скорость наиболее массивного тела.

¨Масса — это мера инертности тела при поступательном движении. Единица массы в СИ — килограмм (кг).

Масса — аддитивная величина, т.е. масса системы равна сумме масс тел, входящих в эту систему.

Источник