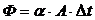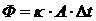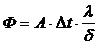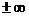Связь между параметрами для изохорного процесса имеет вид

Блог об энергетике

энергетика простыми словами

Основные термодинамические процессы

Основными процессами в термодинамике являются:

Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.

При исследовании термодинамических процессов определяют:

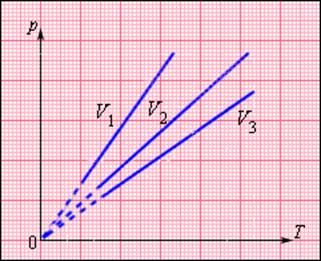
Изохорный процесс

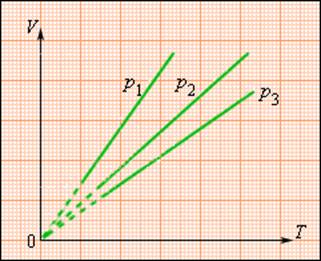
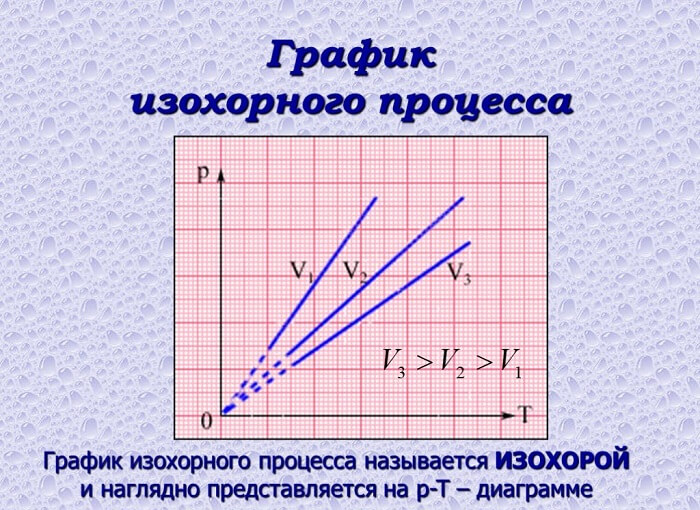
При изохорном процессе выполняется условие v = const.

Из уравнения состояния идеального газа (pv = RT) следует:

т. е. давление газа прямо пропорционально его абсолютной температуре:

Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).

Количество теплоты, подведенной к рабочему телу в процессе 1-2 при c_v = const определяется по формуле:

Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:

Изменение энтропии в изохорном процессе определяется по формуле:

Изобарный процесс

Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:

т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.

Работа будет равна:

Количество теплоты при c_p = const определяется по формуле:

Изменение энтропии будет равно:

Изотермический процесс

При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:

т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.

Работа процесса будет равна:

Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:

При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.

Изменение энтропии равно:

Адиабатный процесс

Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:

В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.

Обозначим теплоемкость в адиабатном процессе через c_ад, и условие dq = 0 выразим следующим образом:

Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (c_ад = 0).

и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:

В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).

k_{выхлопных газов ДВС} = 1,33

Из предыдущих формул следует:

Техническая работа адиабатного процесса (l_техн) равна разности энтальпий начала и конца процесса (i₁ – i₂).

Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.

Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.

Политропный процесс

Политропным называется процесс, который описывается уравнением:

Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:

Работа расширения газа в политропном процессе равна:

В случае идеального газа эту формулу можно преобразовать:

Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:

представляет собой теплоемкость идеального газа в политропном процессе.

При c_v, k и n = const c_n = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.

Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.

Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.

pv 0 = const (n = 0) – изобара;

pv = const (n = 1) – изотерма;

p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;

n > 0 – гиперболические кривые,

n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.

Источник

Уравнение состояния идеального газа. Изопроцессы

Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.

Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:

Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.

Если имеется смесь невзаимодействующих газов, то формулу запишем как:

Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:

Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.

Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.

При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.

Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.

Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.

Источник

Уравнение состояния идеального газа. Изопроцессы

связывающее давление газа с его температурой и концентрацией молекул, получено в 3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства

Здесь N – число молекул в сосуде, N_А – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

Произведение постоянной Авогадро N_А на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:

называется уравнением состояния идеального газа.

Для одного моля любого газа это соотношение принимает вид:

Если температура газа равна T_н = 273,15 К (0 °С), а давление p_н = 1 атм = 1,013·10 5 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V₀, равный

V₀ = 0,0224 м 3 /моль = 22,4 дм 3 /моль.

Это утверждение называется законом Авогадро.

Для смеси невзаимодействующих газов уравнение состояния принимает вид

где ν₁, ν₂, ν₃ и т. д. – количество вещества каждого из газов в смеси.

Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Бенуа Клайпероном, в форме (*) оно было впервые записано Дмитрием Ивановичем Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.

Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.

Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены на диаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.

Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.

Изотермический процесс (T = const)

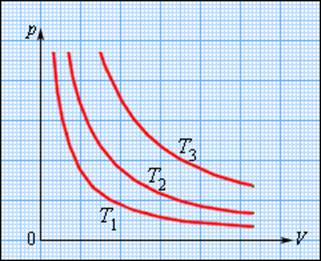
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:

На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гипербол p

1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Робертом Бойлем (1662 г.) и независимо французским физиком Эдмом Мариоттом (1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.

Изохорный процесс (V = const)

Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.

Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p

На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема V изображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).

Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.

Уравнение изохорного процесса может быть записано в виде:

Изобарный процесс (p = const)

Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.

Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:

На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Жозефом Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.

Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.

Источник

Какой процесс называется изохорным

Какой процесс называется изохорным, условия протекания

Изохорным процессом называют термодинамический процесс, протекающий при условии постоянного объема.

Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.

История возникновения теории, кто открыл, формула

Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.

График изохорного процесса в идеальном газе

Зависимость характеристик при изохорном процессе можно представить схематично. График на диаграмме в системе координат будет иметь следующий вид:

В случае идеального газа графически изохорные процессы будут изображены следующим образом:

Первый закон термодинамики для изохорного процесса

В условиях термодинамического процесса формула элементарной работы имеет следующий вид:

Преобразование данного выражения позволит рассчитать величину полной работы процесса:

Изменение внутренней энергии для идеального газа рассчитывается по формуле:

\(\Delta U=\frac<2>\nu R\Delta T\)

где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:

Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:

где \(c_<\upsilon >^<\mu >\) является молярной теплоемкостью в условиях постоянного объема.

Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:

Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:

Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.

Изменения термодинамических параметров в изохорном процессе

В условиях изохорного процесса наблюдается теплообмен с внешней средой. Данное явление называют изменением энтропии. Из его понятия следует уравнение:

где \(\delta Q\) является элементарным количеством теплоты.

Преобразуя уравнение для расчета количества теплоты в дифференциальный вид, получают следующую формулу:

где \(\nu\) является количеством вещества, а \(\nu c^<\mu >_<\upsilon >\) обозначает молярную теплоемкость в условиях постоянного объема.

Формула микроскопического изменения энтропии в условиях протекания изохорного процесса имеет вид:

Если проинтегрировать последнюю формулу, то расчет полного изменения энтропии выполняют таким образом:

В этой ситуации не представляется возможным вынести определение молярной теплоемкости в условиях стабильного объема за интеграл, так как оно представлено в виде функции, зависящей от температуры.

Применение эффекта изохорного процесса

Идеальный цикл Отто приближенно воспроизведен в конструкции мотора внутреннего сгорания, работающего на бензине. Такты 2-3 и 4-1 при его функционировании представляют собой изохорные процессы. На выходе двигателя совершается работа. Она рассчитывается, как разность работ. К одной из них относят работу, производимую газообразным веществом над поршнем в процессе третьего такта или рабочего хода, к другой – работу, затраченную поршнем во время сжатия газа при втором такте. Таким образом, на примере двигателя, функционирующего, согласно принципу Отто, в системе принудительного сжигания смеси, газообразное вещество сжимается до 7-12 раз.

На рисунке изображен классический двигатель Стирлинга с конструкцией бета-типа, для которой характерно расположение рабочего и вытеснительного поршня в одном цилиндре.

Динамику цикла Отто можно представить в следующем виде:

Цикл Стирлинга также характеризуется наличием двух изохорных тактов. Процесс протекает при дооснащении конструкции двигателя Стирлинга регенератором. Во время прохождения газообразного вещества в одном направлении через наполнитель осуществляется передача тепла от рабочего тела к регенератору. Если газ проходит в обратную сторону, то тепловая энергия передается на рабочее тело. Идеальный цикл Стирлинга достигает обратимости и характеризуется теми же параметрами КПД, что и цикл Карно.

Источник

Укажите номер правильного ответа

1. Уравнение для расчета теплоты в изохорном процессе имеет вид

1) ;

2. Связь между параметрами для изохорного процесса определяется выражением

3. Связь между параметрами изобарного процесса определяется выражением

1) ;

4. Процессы дизельного двигателя в координатных осях T — S представлены на рисунке

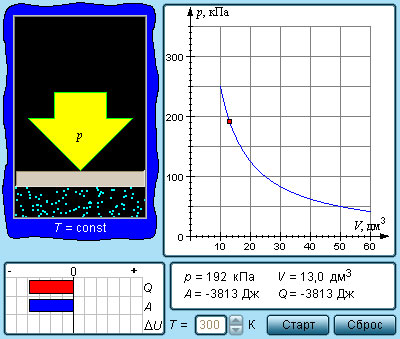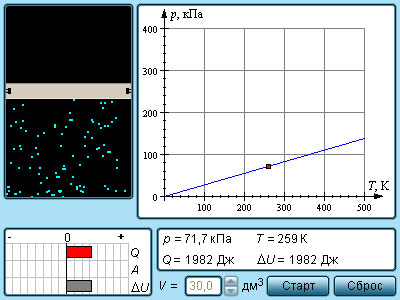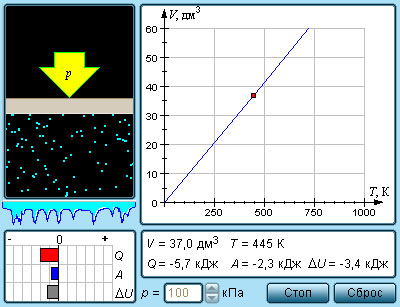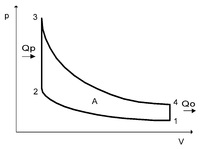
5. Цикл Ренкина в координатных осях P — V представлен на рисунке

6. Уравнение для расчета термического КПД двигателя внутреннего сгорания с подводом теплоты при P = const и v = const имеет вид

1) ;

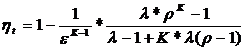
7. Уравнение для расчета термического КПД двигателя внутреннего сгорания с подводом теплоты при v = const имеет вид

1) ;

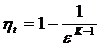
8. Уравнение для расчета КПД цикла Ренкина имеет вид

9. Цикл Отто в координатных осях T — S представлен на рисунке

10. Уравнение для расчета КПД цикла Карно имеет вид

1) ;

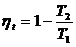
11. Процесс расширения газа, в котором совершается наибольшая работа, показан на графике

12. Цикл Карно в координатных осях T – S представлен на рисунке

13. Связь между параметрами изотермического процесса определяется выражением

1) ;

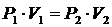
14. Процесс, имеющий минимальный теплообмен, показан на графике

15. Изотермический процесс показан на графике

16. Процессам, в которых подводится теплота, соответствует график

17. При нагревании газа больше изменится энтропия в процессе

18. Уравнение работы для изотермического процесса имеет вид

1) ;

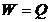
19. Уравнение для изменения энтропии в изохорном процессе имеет вид

1) ;

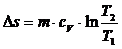
20. Уравнение для изменения энтропии в адиабатном процессе

1) ;

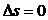
21. Адиабатный процесс показан на графике

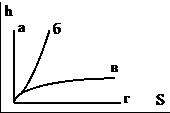
22. Закону Ньютона – Рихмана соответствует уравнение

1) ;

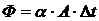
23. Уравнение теплопередачи имеет вид

1) ;

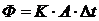
24. Закону теплопроводности (Фурье) соответствует уравнение

1) .

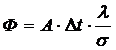
25. Показатель адиабаты К определяется выражением

1) ;

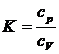
26. Передача теплоты от одной среды другой через стенку называется

27. В абсорбционных холодильных установках в качестве хладона используется

28. Сухой насыщенный водяной пар имеет степень сухости

1) ;

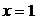
29. Процесс парообразования проходит при

1) и .

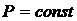
30. Критерий Нуссельта характеризует

1) интенсивность теплоотдачи;

31. Критерий Рейнольдса характеризует

3) режим вынужденного движения;

32. Критерий Грасгофа характеризует

1) подъемную силу при естественной конвекции.

33. Критерий Прандля характеризует

1) физические свойства подвижной среды;

34. Горючими элементами твердого и жидкого топлива являются

1) ;

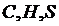
35. При расчете тепловых потерь через пол площадь пола разделяют на зоны шириной

36. При дросселировании идеального газа остается постоянным

37. Минимальная работа в компрессоре затрачивается, если сжатие

38. Основные тепловые потери через ограждение определяются по формуле

1) ;

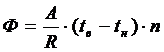
39. Тепловые потери на отопление здания по укрупненным показателям определяются по формуле

1) ;

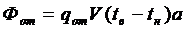
40. Значение удельной отопительной характеристики здания q _от зависит от

1) объема и назначения здания;

41. Наиболее совершенными являются ледники

1) с боковым расположением льда.

42. В животноводческом помещении необходимый воздухообмен (м 3 /час), исходя из допустимого содержания водяных паров, вычисляется по формуле

1) ;

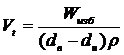
1) ;

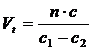
44. В животноводческом помещении необходимый воздухообмен (м 3 /час) по избыточной теплоте рассчитывают по формуле

1) ;

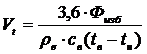
45. Математическое выражение первого закона термодинамики для изолированных систем имеет вид

1) .

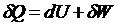
46. Уравнение первого закона термодинамики через энтальпию имеет вид

1) ;

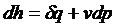
47. Уравнение политропного процесса имеет вид

1) ;

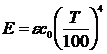
4 9. В вакууме процесс переноса теплоты осуществляется

1) тепловым излучением;

50. Наибольшее значение теплопроводности имеют

51. В котельных установках деаэрация воды производится

1) для удаления растворенных газов;

52. В котельных установках катионитовые фильтры предназначены

1) для умягчения воды;

53. Значение показателя адиабаты зависит от

1) числа атомности газа;

54. Холодильный коэффициент обратимого цикла Карно определяется по формуле

2) ;

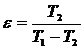
55. Температура кипения воды зависит от

56. Основным горючим элементом твердого и жидкого топлива является

57. Расход теплоты на технологические нужды определяется по формуле

1) ;

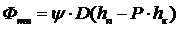
58. Для сгорания 1 кг водорода требуется кислорода

59. Критерий Нуссельта характеризует

1) интенсивность теплоотдачи;

60. Минимальная работа в компрессоре затрачивается, если сжатие

61. Установите соответствие между законом и его математическим выражением

1) Закон Ньютона – Рихмана

а)

2) Закон теплопроводности

б)

г)

62. Установите соответствие между процессом и показателем политропы n

Показатель политропы n

а) n =

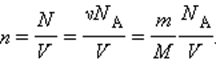
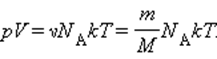
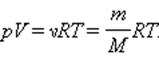
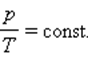
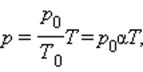
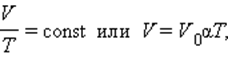
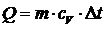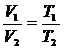Источник