Зная что число 13xy45z делится на 792 найдите x y z
Нужны решения по линейной алгебре, кто соображает помогите плиз, мне нужно понять как решаются некотрые вещи.
1) Очевидно, что речь идёт о 5-значных числах (в противном случае задача совсем банальна: если 135xy — это произведение, то 135xy = 45 * (3xy) — делится на 45 при любых целых x и y).
Итак, считаем, что 135xy — пятизначное число, тогда оно равно 100*135+(10x+y) = 45*300 + (10x+y). Первое слагаемое (45*300) делится на 45, значит на 45 должно делиться и второе слагаемое (10x+y):
10x+y = 45z; причём 0 = 3, то 45z >= 135 — этот вариант нас не устраивает. Остаются значения z = 0, 1 и 2. Все три удовлетворяют условиям задачи; получаем
ОТВЕТ: 13500; 13545; 13590
================================================================================
2. Разложим 700 на простые множители:
700 = 2^2 * 5^2 * 7
Если число a является делителем 700, то оно может быть записано в виде
a = 2^p * 5^q * 7^r,
где p и q могут принимать значения от 0 до 2; r — 0 или 1. Значит, возможны три различных значения p, три значения q и два значения r.
Общее количество комбинаций (а значит, и делителей 700) равно 3*3*2 = 18.
q = 0: имеем делители вида (2^p * 7^r): 1, 2, 4, 7, 14, 28 — их сумма равна 56.
При q=1 и q=2 имеем делители, пропорциональные первому списку: соответственно, в 5 и 25 раз их бОльшие.
Сумма всех делителей числа 700 равна (1+5+25)*56 = 31*56 = 1736
ОТВЕТ: 18 делителей; сумма 1736
Найти все числа вида 135xy делящиеся на 45
45=9*5
если 135xy оканчивается 5 и делится на 9 то и на 45 тоже делится.
Найти сумму и число делителей числа 700
700=2*2*5*5*7
ну дальше то просто ))
По признаку делимости на 5 могут быть две возможности:
а) при у=0, будет х=0 или х=9
б) при у=5, (х+5) делится на 9 только если х=4.
Итак, возможны случаи: 13500, 13590, 13545.
Сумма простых делителей =21, число простых делителей=5.
Если вопрос о любых делителях, то надо покомбинировать их из простых.
Зная что число 13xy45z делится на 792 найдите x y z
Целые числа x, y и z таковы, что (x – y)(y – z)(z – x) = x + y + z. Докажите, что число x + y + z делится на 27.
Решение
Если числа x, y и z дают различные остатки при делении на 3, то число (x – y)(y – z)(z – x) не делится на 3, а число x + y + z, наоборот, делится на 3. Следовательно, по крайней мере, два из трёх чисел x, y, z дают одинаковые остатки при делении на 3. Но тогда число x + y + z = (x – y)(y – z)(z – x) делится на 3, а для этого необходимо, чтобы и третье число давало тот же остаток при делении на 3, что и первые два числа.
Итак, числа x, y, z дают одинаковые остатки при делении на 3. Значит, число x + y + z = (x – y)(y – z)(z – x) делится на 27.
Замечания
Отметим, что такие числа x, y, z существуют, например, 15, 18 и 21 или 50, 53 и 59.
Источники и прецеденты использования
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 1993 |
| Этап | |
| Вариант | 5 |
| класс | |
| Класс | 9 |
| задача | |
| Номер | 93.5.9.5 |
| олимпиада | |
| Название | Всероссийская олимпиада по математике |
| год | |
| Год | 1993 |
| Этап | |
| Вариант | 5 |
| класс | |
| Класс | 10 |
| задача | |
| Номер | 93.5.10.5 |
| олимпиада | |
| Название | Московская математическая регата |
| год | |
| Год | 2010/11 |
| Класс | |
| Класс | 10 |
| задача | |
| Номер | 10.3.3 |
Зная что число 13xy45z делится на 792 найдите x y z
2. Найдите наибольшее значение выражения 3sin^5x-4cos^5x, если x удовлетворяет равенству 2(sin^2x-sinx)+cos^2x-cos^3x=0.
4. На гипотенузе AB прямоугольного треугольника ABC внешним образом построен равнобедренный треугольник AMB (BM=AM=5). Найдите максимальную длину отрезка CM, если \angle BAC=arcsin\frac<3><5>.
5. Найдите все значения a и b, при которых уравнения x(x^2-2x-7)=a и x(x^2+3x-2)=b имеют два общих корня. В ответе укажите наибольшее возможное значение a+b.
6. Найдите количество 6-значных чисел, произведение цифр которых делится на 63.
7. Пусть x,y,z – натуральные числа. Известно, что произведение xy^2z^3=1089994752. На какую максимальную степень двойки может делиться x^2+y^2+z^2?
8. В ряд в порядке возрастания выписали все семизначные числа. Потом те из них, в записи которых встречаются цифры 0, 7, 8 или 9, вычеркнули. Какое число будет стоять на 201123 месте?
9. Вершина A основания ABCD правильной пирамиды SABCD совпадает с вершиной конуса, вершины B и D лежат на его боковой поверхности, вершина S – на окружности основания этого конуса, а вершина C – в плоскости его основания. Найдите объем конуса, если объем пирамиды равен \frac<6><\sqrt2\pi>.
10. Коля сложил 27 чисел, в десятичной записи которых используется одна и та же цифра N и не используются никакие другие цифры. Какое наименьшее число, большее 6521315190, он мог получить?
Зная что число 13xy45z делится на 792 найдите x y z
Задача 15:
Найдите остатки от деления
а) 1989 1990 1991 + 1992³ на 7;
Решение:
Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Решение:
Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.
Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.
Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.
Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.
Задача 17:
Докажите, что n 5 + 4n делится на 5 при любом натуральном n.
Решение:
Указание: Переберите остатки от деления на 5.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 3.
Задача 19:
Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 9.
Задача 20:
Докажите, что n³ – n делится на 24 при любом нечетном n.
Решение:
Указание: Докажите, что указанное число делится и на 3, и на 8.
Задача 21:
а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Решение:
Указание: Докажите, что указанные числа делятся и на 3 и на 8.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Решение:
Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Решение:
Проверьте, что и a и b делятся и на 3 и на 7.
Задача 24:
a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Решение:
Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Решение:
Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Решение:
Выясните возможные остатки квадратов при делении на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Решение:
Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.
Задача 28:
Решение:
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 9 = 81), а за 1 – 9 (1 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.
Задача 29:
Решение:
Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.
Задача 30:
Решение:
Задача 31:
Найдите остаток от деления 2¹ºº на 3.
Решение:
Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».
Задача 32:
Найдите остаток от деления 3 1989 на 7.
Решение:
Задача 33:
Докажите, что 2222 5555 + 5555²²²² делится на 7.
Решение:
Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.
Задача 34:
Найдите последнюю цифру числа 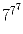
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Решение:
Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Решение:
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Решение:
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Решение:
Рассмотрите остатки по модулю 3.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:
Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Решение:
Это число дает остаток 7 от деления на 9.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Решение:
Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Решение:
Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
Решение:
Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.
