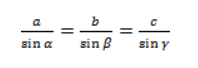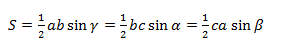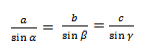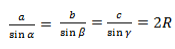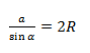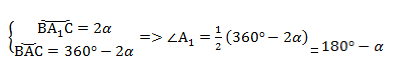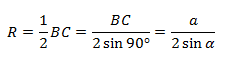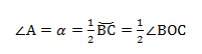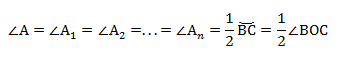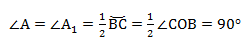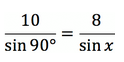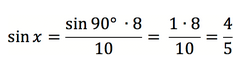Что будет если sin умножить на sin
Ещё немного о тригонометрии в вычислениях
На Хабре было уже много статей, посвящённых быстрым вычислениям тригонометрии, когда сильно надо, но я хотел бы дополнить их одной небольшой заметкой с отсылкой к школьной тригонометрии.
Иногда может не быть аппаратной реализации тригонометрии, иногда могут быть иные причины, чтобы изобретать методы ускорения вычисления.
Математика
Давайте вспомним некоторые простые формулы из школьного курса.
Начнём с простых:
(1)
Косинус/синус любого угла может быть приведён к аргументу в диапазоне от 0° до 45°, используя формулы первой группы.
Для малых углов тригонометрические функции могут быть сведены к асимптотическим разложениям, если отбрасываемые члены заведомо выходят за разрядную сетку.
Все промежуточные углы могут быть получены суммированием больших углов с некоторым шагом (а для них тригонометрию можно считать таблично), и остатков, которые рано или поздно дадут линейное разложение.
Применение
Дальше нужно будет выбрать шаг таблиц исходя из того, как мы хотим распределить вычисления, показатель степени 11 мы разделим на несколько частей. Например, можно разбить его на две части: 11=6+5, тогда нам понадобятся две таблицы размером 64 и 32 записи (итого 96), или на три части: 11=4+4+3 (размер таблиц 16+16+8=40 записей), но будет больше операций умножения — конкретный выбор будет зависеть от задачи и располагаемых ресурсов.
Ремарка: запись в таблице — это пара синус и косинус аргумента. Если храним с одинарной точностью, то размер записи 8 байт.
Пример
Давайте для примера возьмём разложение 4+4+3, а потом обобщим.
Шаг 1. Приведём аргумент x к нашей шкале, поделив его на константу pi/4 (назовём его x’ ).
[предположим для примера, что получился синус]
Шаг 3. Воспользуемся таблицами (напомню, что их 3), при этом индексами в таблице будут «битовые поля» в двоичном представлении аргумента x» — первые 4 бита после запятой, потом ещё 4, и ещё 3, а оставшиеся не при делах биты пойдут в остаток.
Табличные синус назовём S1, S2, S3, табличные косинусы — C1, C2, C3.
Шаг 4. Объединяем всё, что получилось:
Шаг 5. Если на шаге 2 мы сочли, что результат должен получиться отрицательным, то этот минус надо ввести в результат.
Заключение
Аналогичный подход может использоваться как для вычисления в вещественных числах любого размера, так и, например, для реализации специализированной арифметики с фиксированной запятой. Собственно, в своё время именно последняя задача меня и сподвигла поковыряться в эту сторону, но это было давно.
Теорема синусов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Вспомним свойство вписанного в окружность четырёхугольника:
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
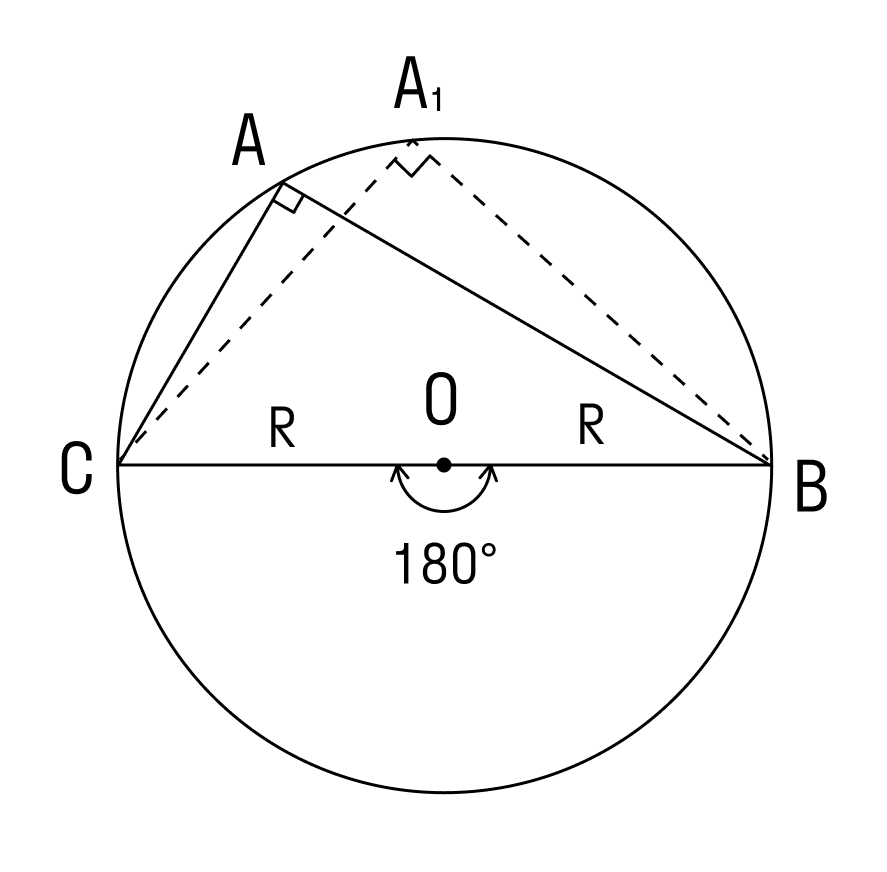
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
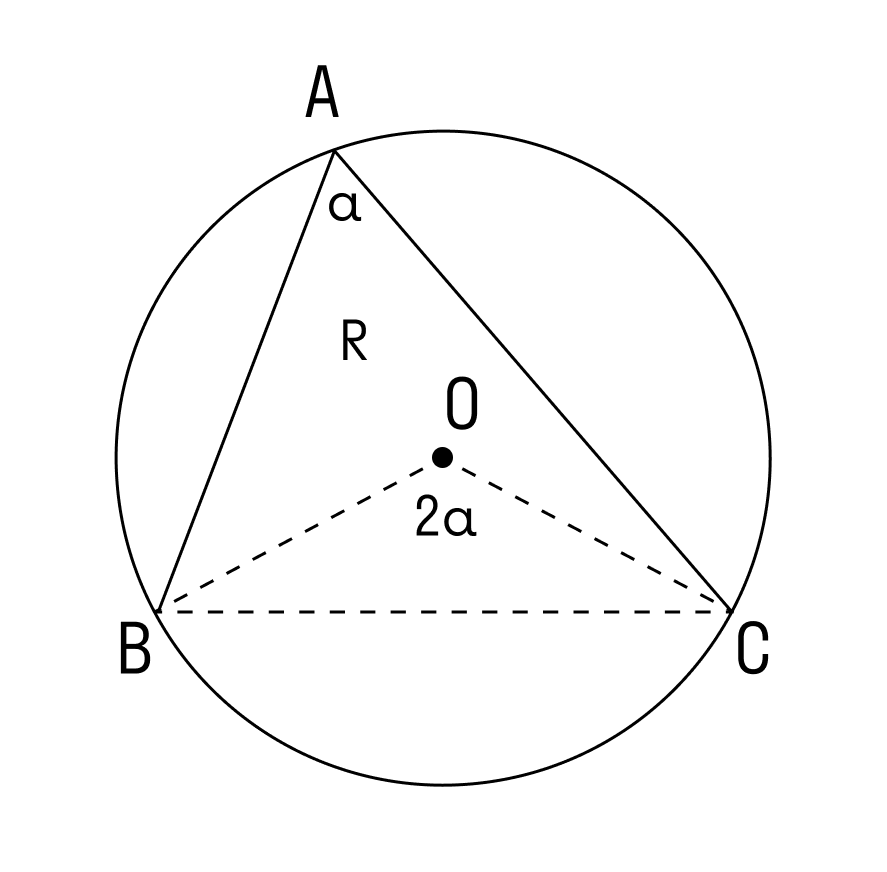
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
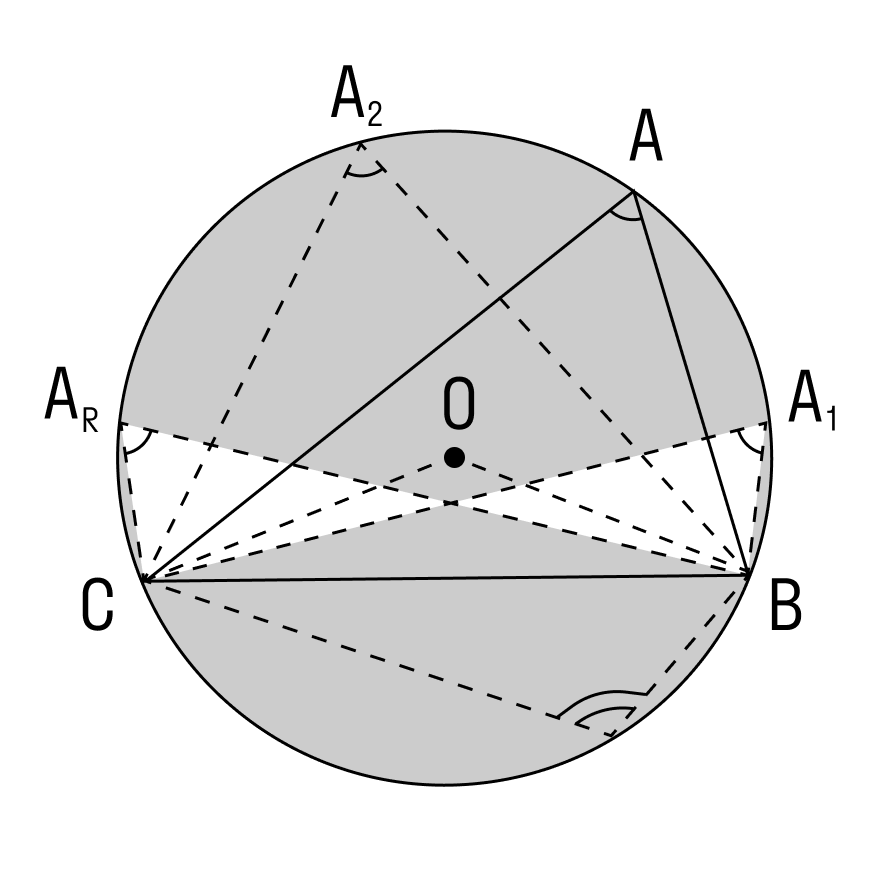
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>