дитеринг что это такое

Дизеринг: зашумляем сигнал, чтобы улучшить его

Введение

В первой части этой серии статей мы рассмотрим теоретическую сторону дизеринга, немного истории и применение его к 1D-сигналам и дискретизации. Я попытаюсь провести частотный анализ ошибок дискретизации и расскажу о том, как дизеринг помогает их исправить. В основном это будет теоретическая статья, поэтому если вам интересны более практические применения, то ждите следующих частей.

Блокнот Mathematica для воспроизведения результатов можно найти здесь, а pdf-версия находится здесь.

Что такое дизеринг?

Дизеринг (Dithering) можно описать как намеренное/осознанное внесение в сигнал шума для предотвращения ошибок большого масштаба/низкого разрешения, возникающих вследствие дискретизации или субдискретизации.

Если вы когда-нибудь работали с:

Однако я обнаружил в Википедии довольно удивительный факт о том, как впервые был определён и использован дизеринг:

— Кен Полманн, Principles of Digital Audio

Это вдохновляющий и интересный исторический факт и мне понятно, почему он позволяет избегать отклонений в вычислениях и резонансах, случайным образом разрушая циклы обратной связи механической вибрации.

Но хватит истории, давайте для начала рассмотрим процесс дизеринга в 1D-сигналах, например, в аудио.

Дискретизация дизерингом постоянного сигнала

Мы начнём с анализа самого скучного в мире сигнала — постоянного сигнала. Если вы знаете немного о цифровой обработке сигналов, связанных со звуком, то можете сказать: но ты же обещал рассмотреть аудио, а в звуке по определению нет постоянной составляющей! (Более того, и в ПО, и в оборудовании обработки звука намеренно устраняется так называемый сдвиг постоянной составляющей (DC offset).)

Это правда, и вскоре мы рассмотрим более сложные функции, но начнём мы сначала.

Представьте, что мы выполняем 1-битную дискретизацию нормализованного сигнала с плавающей запятой. Это значит, что мы имеем дело только с конечными двоичными значениями, 0 или 1.

Если сигнал равен 0,3, то простое округление без дизеринга будет самой скучной функцией — просто нулём!

Погрешность тоже постоянна и равна 0,3, следовательно, и средняя погрешность равна 0,3. Это означает, что мы внесли довольно большое отклонение в сигнал и полностью потеряли информацию исходного сигнала.

Мы можем попробовать выполнить дизеринг этого сигнала и посмотреть на результаты.

Дизеринг в этом случае (при использовании функции округления) просто применяет обычный случайный белый шум (случайное значение для каждого элемента, что создаёт равномерный спектр шума) и прибавляет в сигнал перед дискретизацией случайное в интервале (-0.5, 0.5).

quantizedDitheredSignal =
Round[constantSignalValue + RandomReal[] – 0.5] & /@ Range[sampleCount];

Здесь сложно что-то увидеть, теперь результат дискретизации — это просто набор случайных единиц и нулей. С (ожидаемо) большим количеством нулей. Сам по себе этот сигнал не особо интересен, однако довольно интересен график погрешностей и средняя погрешность.

Итак, как мы и ожидали, погрешность тоже варьируется, но пугает то, что погрешность иногда стала больше (абсолютное значение 0,7)! То есть максимальная погрешность к сожалению стала хуже, однако средний шум имеет значение:

Намного лучше, чем первоначальная погрешность в 0,3. При значительно большом количестве сэмплов эта погрешность будет стремиться к нулю (к пределу). Итак, погрешность постоянной составляющей стала намного меньше, но давайте взглянем на частотный график всех погрешностей.

Красный график/всплеск = частотный спектр погрешности при отсутствии дизеринга (постоянный сигнал без частот). Чёрный — с дизерингом при помощи белого шума.

Всё становится интереснее! Это демонстрирует первый вывод из этого поста — дизеринг распределяет погрешность/отклонение дискретизации среди множества частот.

В следующем разделе мы узнаем, как это нам поможет.

Частотная чувствительность и низкочастотная фильтрация

Выше мы наблюдали за дизерингом дискретизированного постоянного сигнала:

Более того, наши медиаустройства становятся всё лучше и лучше, обеспечивая большую избыточную дискретизацию (oversampling). Например, в случае телевизоров и мониторов у нас есть технология «retina» и 4K-дисплеи (на которых невозможно разглядеть отдельный пиксель), в области звука мы используем форматы файлов с дискретизацией не менее 44 кГц даже для дешёвых динамиков, которые часто не могут воспроизводить больше, чем 5-10 кГц.

Это значит, что мы можем аппроксимировать воспринимаемый внешний вид сигнала, выполнив его низкочастотную фильтрацию. На графике я выполнил низкочастотную фильтрацию (заполнение нулями слева — это «нарастание»):

Красный — желаемый недискретизированный сигнал. Зелёный — дискретизированный сигнал с дизерингом. Синий — низкочастотный фильтр этого сигнала.

Сигнал начинает выглядеть гораздо более близким к исходной, недискретизированной функции!

К сожалению, мы начинаем видеть низкие частоты, которые очень заметны и отсутствуют в исходном сигнале. В третьей части серии мы попробуем исправить при помощи синего шума. А пока вот как график может выглядеть с функцией псевдо-шума, имеющей содержимое с гораздо меньшей частотой:

Это возможно, потому что наша псевдослучайная последовательность имеет следующий спектр частот:

Но давайте закончим рассматривать простые, постоянные функции. Взглянем на синусоиду (если вы знакомы с теоремой Фурье, то знаете, что она является строительным блоком любого периодического сигнала!).

Дискретизация синусоиды

Если мы дискретизируем синусоиду 1-битной дискретизацией, то получим простой прямоугольный сигнал.

Прямоугольный сигнал довольно интересен, потому что включает в себя и базовую частоту, и нечётные гармоники.

Это интересное свойство, которое активно используется в аналоговых субтрактивных синтезаторах для создания звучания полых/медных инструментов. Субтрактивный синтез берёт сложный, гармонически богатый звук и фильтрует его, устраняя некоторые частоты (параметры фильтра варьируются со временем), чтобы придать звукам нужную форму.

Спектр частот прямоугольного сигнала:

Но в этом посте нас больше интересую погрешности дискретизации! Давайте создадим график погрешности, а также спектр частот погрешности:

В этом случае ситуация гораздо лучше — средняя погрешность близка к нулю! К сожалению, у нас по-прежнему присутствует множество нежелательных низких частот, очень близких к нашей основной частоте (нечётных множителей с уменьшающейся величиной). Это явление называется алиасингом или шумом дизеринта — возникают частоты, отсутствовавшие в исходном сигнале, и они имеют довольно большие величины.

Даже низкочастотная фильтрация не сможет значительно помочь сигналу. Погрешность имеет очень много низких частот:

Дискретизированная синусоида с низкочастотной фильтрацией

Погрешность дискретизированной синусоиды с низкочастотной фильтрацией

Давайте взглянем, как меняется ситуация при добавлении дизеринга. На первый взгляд, улучшений почти нет:

Однако если мы рассмотрим это как изображение, то оно начинает выглядеть лучше:

Заметьте, что погрешности дискретизации снова распределены среди различных частот:

Выглядит очень многообещающе! Особенно учитывая то, что теперь мы можем попробовать выполнить фильтрацию:

Это немного искажённая синусоида, но она выглядит намного ближе к исходной, чем версия без дизеринга, за исключением фазового сдвига, внесённого асимметричным фильтром (я не буду объяснять этого здесь; скажу только, что проблему можно устранить, применив симметричные фильтры):

Красный — исходная синусоида. Зелёный — подвергнутый низкочастотной фильтрации сигнал без дизеринга. Синий — подвергнутый низкочастотной фильтрации сигнал с дизерингом.

Графики обеих погрешностей численно подтверждают, что погрешность намного меньше:

Красный — погрешность подвергнутого низкочастотной фильтрации сигнала без дизеринга. Синий — погрешность подвергнутого низкочастотной фильтрации сигнала с дизерингом.

Наконец, давайте вкратце рассмотрим сигнал с более качественной функцией дизеринга, содержащей только высокие частоты:

Верхнее изображение — функция белого шума. Нижнее изображение — функция, содержащая более высокие частоты.

Версия с низкочастотной фильтрацией, дизерингом и улучшенной функцией — почти идеальные результаты, если не учитывать фазовый сдвиг, вызванный фильтром!

И наконец, сравнение всех трёх спектров погрешностей:

Красный — спектр погрешности дискретизации без дизеринга. Чёрный — спектр погрешности дискретизации с дизерингом белым шумом. Синий — спектр погрешности дискретизации с дизерингом с более высокими частотами.

На этом первая часть серии заканчивается. Основные выводы:

Источник

Дитеринг что это такое

Мы создали специальную тему в конференции, где собрали вопросы по теме «Дизеринг и нойз-шейпинг». Любой желающий мог задать свой вопрос Алексею Лукину, известному эксперту по цифровой обработке сигналов, разработчику алгоритмов компании iZotope (США). К вопросам читателей мы добавили и несколько редакционных. Благодарим читателей за активное участие!

Введение

Преобразование звукового сигнала из аналоговой в цифровую форму можно представить в виде двух этапов: дискретизации по времени и квантования по амплитуде. На первом этапе (дискретизация) мгновенные значения сигнала замеряются с некоторым шагом по времени. На втором этапе (квантование) каждое из измеренных значений сигнала представляется в виде числа с некоторой точностью — разрядностью квантования.

На заре цифровой звукозаписи бытовало представление о разрушительном действии оцифровки на звуковой сигнал. И даже сейчас можно услышать мнение, что искажения в цифровом звуке зависят от уровня сигнала. В этой статье мы рассмотрим, как возникают искажения квантования и как их можно предотвратить.

Квантование сигнала

В начале эпохи цифровой звукозаписи разрядность АЦП и ЦАП была невысокой: 8 либо 16 бит в бытовой технике и 16–18 бит в профессиональной. Эффективных алгоритмов компрессии (типа mp3) еще не существовало, дисковое пространство было дорогим, а интернет — медленным. Поэтому нередко первые цифровые звукозаписи распространялись в формате 8 бит. Всем, конечно, знаком их хрустящий и искаженный звук. Вскоре 8-битный формат сменился 16-битным CD-форматом, и качество звука значительно выросло. Однако даже при 16-битном квантовании требуется уделять внимание возможным искажениям тихих звуков.

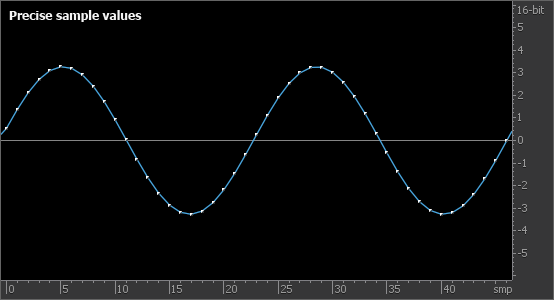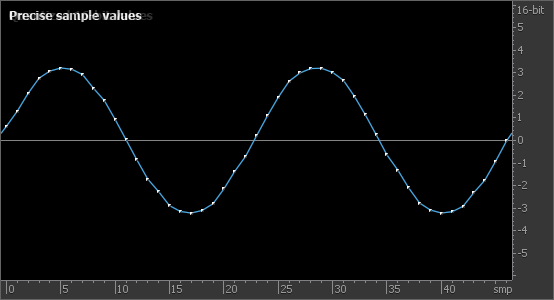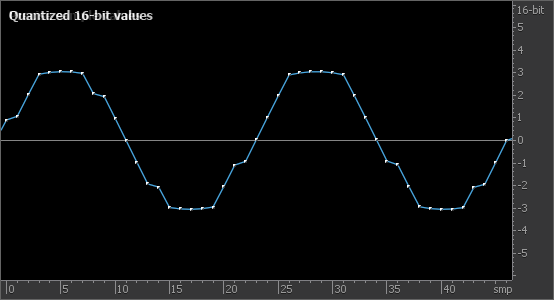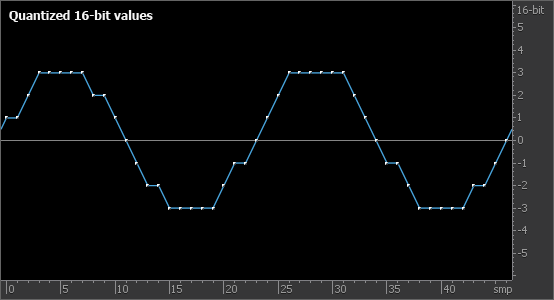
При квантовании сигнала амплитуда каждого отсчета округляется до ближайшего значения разрядной сетки (рис. 1). Нетрудно видеть, что для звуков малой амплитуды это может приводить к значительному искажению формы сигнала (рис. 2). Такой простейший способ квантования называется усечение (truncate, транкейт) либо округление (rounding).

Разница между исходным и квантованным сигналом называется ошибкой квантования или шумом квантования. Для сигналов малой амплитуды ошибка квантования сильно коррелирует с сигналом, что приводит к нелинейным искажениям и грязному звучанию (в этом смысле, термин «шум квантования» не очень удачен, так как ошибка квантования не похожа на шум). При 16-битном квантовании мощность ошибки квантования составляет приблизительно −98 дБ RMS (за 0 дБ RMS принимается мощность синусоиды максимального уровня, согласно стандарту AES-17).

Дитеринг

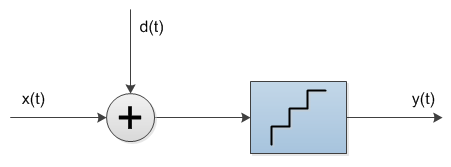
К счастью, существует метод сделать ошибку квантования практически не зависимой от исходного сигнала. Он называется английским словом дитеринг (dithering, в русской транскрипции также встречается «дизеринг») и заключается в подмешивании к сигналу шума перед квантованием (рис. 3).

Амплитуда шума дитеринга выбирается особым образом, чтобы устранить нелинейные искажения при последующем квантовании. Если амплитуда дитеринга мала, то нелинейные искажения будут устранены не полностью, либо амплитуда ошибки квантования будет меняться вместе с сигналом. Если амплитуда дитеринга велика, то шум станет заметным в записи.

Наиболее распространенным типом дитеринга является стандартный TPDF-дитеринг — белый шум с пиковой амплитудой ±1 LSB (least significant bit — шаг квантования) и треугольным распределением вероятности амплитуд. Почти любая цифровая рабочая станция (DAW) умеет генерировать дитеринг такого типа.

Важным моментом в применении дитеринга является его добавление к сигналу до, а не после квантования. Неправильно понимать дитеринг как шум, скрывающий или маскирующий искажения квантования. На самом деле дитеринг предотвращает появление искажений. Попытка замаскировать уже возникшие искажения потребовала бы шума значительно большей амплитуды.

Продемонстрируем работу дитеринга на тестовом сигнале «плавающий синус» с уровнем −80 дБ и плавным затуханием в конце (рис. 4). Для лучшей слышимости искажений сигнал после квантования в 16 бит был усилен на 55 дБ. Будем изучать как форму волны, так и спектрограмму.

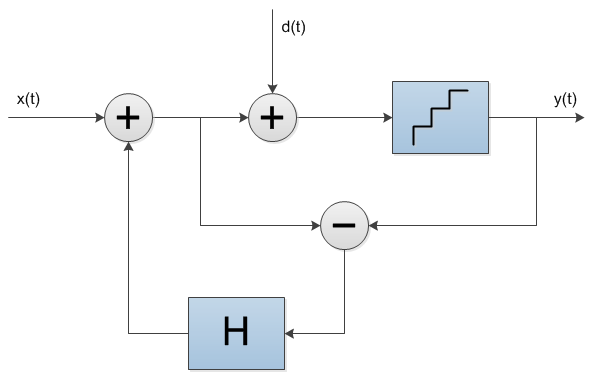
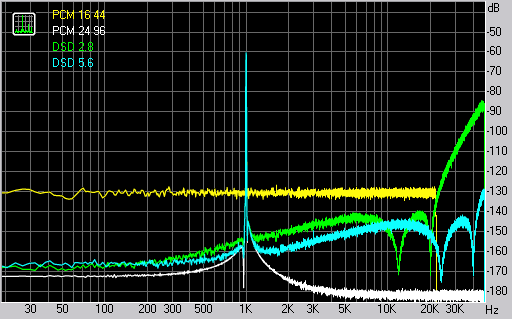
наведите мышь для смены картинки На спектрограмме сигнала, квантованного без дитеринга, видны сильные нелинейные искажения, усиливающиеся при уменьшении уровня сигнала. В конце записи сигнал полностью исчезает, так как его амплитуда становится меньше половины шага квантования. Спектрограмма с дитерингом показывает, что после квантования искажений в сигнале не появилось, а добавившийся шум однороден. Однако его мощность превышает мощность искажений при транкейте (−98 дБ) и составляет −93 дБ. Нойз-шейпинг Повышенная мощность ошибки квантования при дитеринге порождает вопрос: можно ли проводить дитеринг не белым шумом, а таким, который будет менее заметен? Например, высокочастотным шумом. К сожалению, напрямую этот метод не работает. Если вместо белого шума дитеринга подмешать окрашенный шум, то ошибка квантования все равно будет близка к белому шуму. Кроме того, существует опасность неполного подавления нелинейных искажений квантования. Чтобы придать спектру ошибки квантования нужную форму, существует более сложный метод, называемый нойз-шейпингом (noise shaping, формирование спектра шума). В этом методе присутствует обратная связь: разница между квантованным и исходным сигналами пропускается через фильтр и прибавляется к следующему отсчету сигнала (рис. 5). Варьируя частотную характеристику фильтра, можно добиться нужного спектра ошибки квантования. Наиболее часто ошибку квантования вытесняют в диапазон высоких частот и ультразвука, где она будет наименее слышна. В слышимом диапазоне частот спектр нойз-шейпинга обычно приблизительно повторяет кривую порога слышимости. При нойз-шейпинге общая мощность ошибки квантования возрастает (по сравнению с дитерингом), но ее субъективная громкость снижается (рис. 4). Чем сильнее требуется снизить мощность шума в слышимой полосе (нижние и средние частоты), тем больше шума появляется в области верхних частот. Слишком большая мощность верхних частот в аудиосигнале нежелательна: она может затруднить последующую обработку сигнала, его кодирование в mp3, восстановление царапин при ошибках чтения с CD. Поэтому при 16-битном квантовании принято использовать нойз-шейпинг, не превышающий по уровню −60 дБ. Снижение субъективной слышимости шума при этом достигает 10–15 дБ по сравнению со стандартным TPDF-дитерингом. Обратите внимание, что файл с нойз-шейпингом звучит чисто. Так же, как при дитеринге, ошибка квантования представляет собой ровный шум без нелинейных искажений, не зависящий от сигнала. Понижение разрядности Квантование сигнала происходит не только при оцифровке звука в АЦП, но и при последующей работе с цифровым сигналом: обработке, преобразовании формата, изменении уровня. Когда сигнал определенной разрядности (например, 16 бит) подвергается пересчету, его разрядность автоматически увеличивается (например, до 32 бит). Далее, если сигнал необходимо записать в файл исходного формата (16 бит), то происходит повторное квантование: из 32 бит в 16. При этом квантовании возможны те же искажения, что и в АЦП. Поэтому процесс дитеринга должен быть встроен в любые программы и алгоритмы, обрабатывающие сигнал. Чтобы минимизировать эффект от операций повторного квантования, обработка сигнала часто происходит в повышенной разрядности (24 или 32 бита), а окончательное снижение разрядности (до 16 бит) применяется после всех остальных операций. Понижение разрядности сигнала используется также в звуковых ЦАП: большинство из них имеют небольшую разрядность (1–5 бит), но высокую частоту дискретизации (порядка 10 МГц). При этом ЦАП заявляется как 24-битный, в том смысле, что он принимает на вход 24-битный аудиосигнал. Но внутри сигнал подвергается передискретизации (oversampling) — повышению частоты дискретизации и понижению разрядности с нойз-шейпингом. Поскольку финальная частота дискретизации очень высока, то в ультразвуковом диапазоне (выше 20 кГц) присутствует много места для шума нойз-шейпинга. Поэтому даже при малой разрядности сигнала (1–5 бит) агрессивный нойз-шейпинг способен создать динамический диапазон порядка 120 дБ в слышимой области частот. На рис. 5 показано сравнение типичных спектров шума нескольких звуковых форматов высокого разрешения: CD-формата (PCM 16 бит, 44 кГц) со стандартным TPDF-дитерингом, формата «24 бита 96 кГц» и двух форматов DSD с различными частотами дискретизации. Поскольку DSD-форматы имеют разрядность 1 бит, в них присутствует значительный нойз-шейпинг. У формата «DSD-2.8 МГц» быстрый подъем мощности шума начинается сразу за 20 кГц. У формата «DSD-5.6 МГц» шум лежит вдвое выше (уже за пределами графика на рис. 5). Квантование изображений Похожие алгоритмы квантования используются и в обработке изображений, когда надо представить цвет малым числом доступных градаций. Проиллюстрируем это на примере 4-битного квантования (16 градаций яркости). наведите мышь для смены картинки

Эффект от простого квантования цветов называется постеризацией: на изображении появляются ложные контуры, а часть деталей исчезает (рис. 6). Постеризации можно избежать, добавив перед квантованием шум дитеринга. Однако более качественного результата достигает алгоритм диффузии ошибки. Аналогично нойз-шейпингу, он вытесняет ошибку квантования в область верхних частот, где чувствительность глаза невысока. Диффузия ошибки часто применяется в офсетной печати для смешивания цветов.

Вопросы и ответы

Нужен ли дитеринг при работе в формате 32-bit float?

Нет, не нужен. Для этого формата не существует правильного дитеринга, так как ошибка квантования зависит от уровня сигнала: она имеет уровень примерно −150 дБ по отношению к уровню каждого отсчета. Точность этого формата составляет примерно 25 бит, так что быстрого накопления ошибок квантования можно не опасаться.

Нужен ли дитеринг при преобразовании из 32-bit float в 24-битный формат?

Да, при квантовании сигнала в разрядность 24 бита (и менее) нужен дитеринг. При 24 битах дитеринг в большинстве случаев не будет заметно влиять на результат, но его применение должно быть автоматическим, без лишних раздумий.

Нужен ли дитеринг при конвертировании файла в mp3?

Все зависит от того, сохраняете ли вы файл с низкой разрядностью перед конвертацией в mp3 или конвертируете в mp3 непосредственно из формата высокой разрядности. Дитеринг нужен для сохранения файла с низкой разрядностью, а не для mp3. Некоторые mp3-кодеры умеют компрессировать звук из форматов с высокой разрядностью, что позволяет избежать лишних конвертаций. Впрочем, артефакты mp3 обычно намного сильнее, чем искажения от конвертации разрядности.

Какой вид нойз-шейпинга использовать?

Это вопрос личных предпочтений и даже отчасти аудиофильский. Многие профессиональные инженеры мастеринга используют стандартный TPDF-дитеринг без нойз-шейпинга с отличными результатами. Другие — имеют предпочтения и считают, что тип нойз-шейпинга влияет на окончательное звучание фонограммы. Например, Боб Кац активно участвовал в создании нескольких режимов нойз-шейпинга MBIT+ для плагина Ozone 5. Я считаю, что в дитеринге и нойз-шейпинге важнее повсеместное и своевременное применение, нежели конкретный вид или алгоритм.

Достаточно ли уже имеющегося в записи шума для дитеринга?

В некоторых случаях — да, но не всегда. Шум дитеринга должен иметь определенные статистические свойства: требуемую мощность в каждой полосе частот, случайность распределения амплитуд. Поэтому надежнее применять дитеринг в любом случае, автоматически и без лишних раздумий.

Что применять сначала: дитеринг или преобразование частоты дискретизации (SRC)?

Так как SRC повышает разрядность сигнала (аналогично любой другой обработке), то сначала выполняется SRC, а затем дитеринг. Причем, между ними необходимо проверить, нет ли клиппирования, так как SRC может повысить пиковый уровень записи.

В статье Н. Сухова «Hi-Fi правда и High-End сказки» написано, что у аналоговой записи на пленке динамический диапазон определяется шумом снизу, а у цифровой — нет, потому что у 16-битного цифрового сигнала динамический диапазон равен 50 дБ из-за шумов квантования, которые дают 1% искажений. Верно ли это?

Статья Н. Сухова была написана в 1998 году, когда понимание дитеринга еще не было повсеместным. В статье рассматривается только случай квантования транкейтом. Однако при корректном использовании дитеринга и нойз-шейпинга никаких нелинейных и интермодуляционных искажений не возникает. При этом динамический диапазон компакт-диска составляет честные 93 дБ, а структура шума такая же, как у магнитной пленки.

Можно ли говорить о том, что нойз-шейпинг увеличивает динамический диапазон в наиболее слышимой СЧ-области?

Да, нойз-шейпинг увеличивает динамический диапазон в области средних частот (либо даже во всем диапазоне 0–15 кГц, в зависимости от алгоритма). В частности, может улучшиться A-взвешенный динамический диапазон.

Вопрос о возможном конфликте нойз-шейпинга в файле и нойз-шейпинга в конвертере. Не повредит ли нойз-шейпинг в исходном файле ЦАП-у с агрессивным нойз-шейпингом?

Нет. Насколько я понимаю, они не мешают друг другу и повсеместно используются вместе.

Благодарим Алексея Лукина за подробные ответы
и за потраченное время на обсуждение в нашей конференции!

Источник